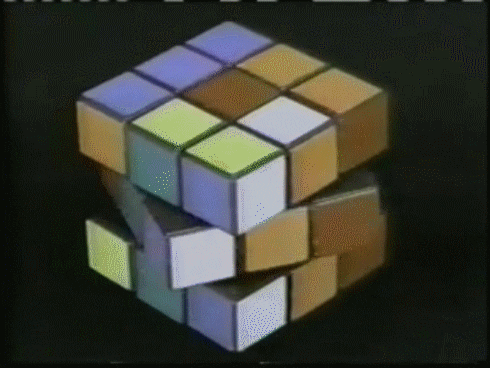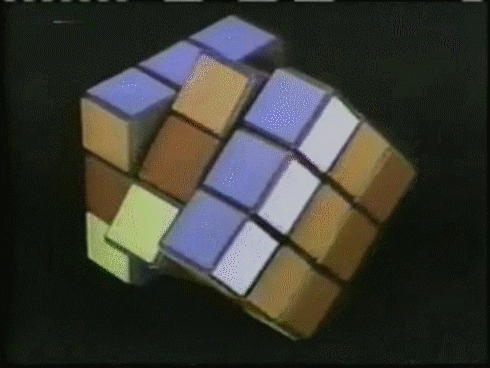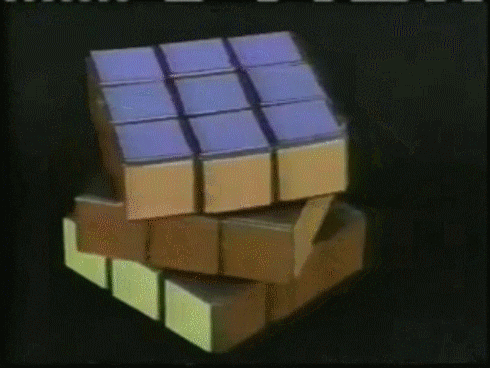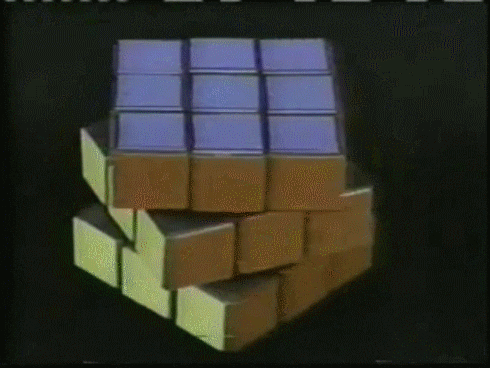Learning To Solve a Rubik’s Cube From Scratch using Reinforcement Learning

Photo by Olav Ahrens Røtne on Unsplash

Motivation :

A Rubik’s cube is a 3D puzzle that has 6 faces, each face usually has 9 stickers in a 3x3 layout and the objective of the puzzle is to achieve the solved state where each face only has a unique color.
The possible states of a 3x3x3 Rubik’s cube are of the order of the quintillion and only one of them is considered the “solved” state. This means that the input space of any Reinforcement Learning agent trying to solve the cube is huuuuuge.

Dataset :

We represent a Cube using the python library pycuber and only consider quarter rotations (90°) moves. No annotated data is used here, all the samples are generated as a sequence of states going from the solved state and then inverted ( so that its going to the solved state) and then those sequences are what is used for training.

Problem Setting :

Flattened Cube

From a randomly shuffled cube like the example above we want to learn a model that is able to output a sequence of actions from the set {‘F’: 0, ‘B’: 1, ‘U’: 2, ‘D’: 3, ‘L’: 4, ‘R’: 5, “F’”: 6, “B’”: 7, “U’”: 8, “D’”: 9, “L’”: 10, “R’”: 11}* (See https://ruwix.com/the-rubiks-cube/notation/ for a definition)* to go to a solved state like the one below :

Flattened solved Cube

Model :

The ideas implemented here is are mostly from the paper Solving the Rubik’s Cube Without Human Knowledge

Figure from “Solving the Rubik’s Cube Without Human Knowledge” by McAleer et al.

The RL approach implemented is called Auto-didactic Iteration or ADI. As illustrated in the figure above (from the paper). We construct a path to the solved state by going backwards from the solved state and then we use a fully connected network to learn the “policy” and “value” for each intermediate state in the path. The learning targets are defined as :

Where “a” is a variable for all the 12 possible action defined in the introduction and R(A(x_i, a)) is the reward achieved by taking action a from state x_i. We define R = 0.4 if we land in solved state and -0.4 otherwise. The reward is the only supervision signal that the network gets during training, which can be delayed by multiple “action” decisions since the only state with a positive reward is the final solved state.

At inference time we use the value-policy network to guide our search for the solved state so that we can solve the puzzle in as little time as possible by reducing the number of actions that are “worth” taking.

Results :

The results I had with this implementation were not as spectacular as what was presented in the paper. From what I noticed, this implementation could easily solve cubes that are 6, 7 or 8 shuffling steps away from the solved state but had a much harder time beyond that.
Example of the network in action :

Conclusion :

This is a pretty cool application of Reinforcement Learning to solve combinatorial problem where the is a huge number of states but without using any prior knowledge or feature engineering.

Code to reproduce the results is available at : https://github.com/CVxTz/rubiks_cube