- 利用Go语言对基础算法进行全面的学习和巩固,以帮助自己以及大家学习数据结构和算法
- 数组
- 数组具有随机访问的特性,因为数组是一组连续分配的内存空间所以,它可以通过下标来进行随机访问
- 数组为什么从零开始
- 从性能上讲,数组的访问是访问地址的偏移量,如果从1开始,需要减去1才是偏移量,为了性能从0开始
- 从历史上讲,第一个人使用了0后人沿用
-
链表
- 是不连续的内存空间,相比数据它的修改(增删改)时间复杂度O(1),但是空间复杂度是翻倍的,单链表是一倍,双链表是两倍
-
栈
- 后进先出的数据结构,只有出栈和入栈两个操作
- 栈的应用
- 函数栈,函数调用是嵌套的,函数内先执行,所以要用栈的结构
- 运算优先级栈,使用两个栈,一个栈直接存数字,另一个栈存运算符,如果入栈的运算符优先级大于或者等于栈顶,从数字 栈中取两个数字进行运算,在存入数字栈中,以此递推
- 判断字符串是否构成封闭对称的结构,以(){}[]这种简单结构为例,从字符串左边依次进行遍历,当有(直接压入栈中,当遇到) 在栈中查找与之匹配的符号,出栈并将其他符号再次压入栈中,如果栈中最后没有剩余符号表示,括号匹配,如果有剩余说明,括号不匹配
- 实现浏览器前进和后退,访问时入栈1,回退时吧1从栈顶依次压入栈2,类似于倒水,从A杯子倒入B杯子
-
堆
- 堆:是一个完全二叉树,可以用数组来保存它。
- 分类:
- 大顶堆:堆顶元素是最大的
- 小顶堆:堆顶元素是最小的
- 堆的应用:
- 优先级队列:用小顶堆实现计时器功能和小文件合并。
- 中位数问题:用两个堆,一个大顶堆一个小顶堆,大顶堆和小顶堆的堆顶是一致的,这个堆顶就想一个分割线,大于他的放入小顶堆,小于他的放入大顶堆
- TopK问题:实现一个长度为K的小顶堆,如果插入元素和它比小于它什么也不做,大于它删除它插入堆顶
-
队列
-
散列表
- 定义:是对数组的扩展,利用数组的随机访问特性,将key值进行hash,将得到的值存入hash表中,hash表就是连续的数组
- 散列函数(哈希函数):将string类型的key转换成int类型,存入hash表
- 散列函数计算后的算列值为非负整数
- 如果key1=key2 ,那么hash(key1)=hash(key2)
- 如果key1≠key2 ,那么hash(key1)≠hash(key2) (很难实现,在数组快要满的情况下,很容易产生冲突)
- 散列冲突:
- 开放寻址方式
- 插入:如果冲突,在冲突点向下查找
- 查找:类似插入,一次向下查找,当查找到空闲位置还没有找到就是说明不存在
- 删除:不是真实删除是标记删除位,防止查询失效
- 探测方法:
- 二次探测
- 多重hash
- 装载因子:装载因子=已填充的个数/hash表长度
- 链表法
- 以槽为单位,将重复的hash值存在槽的链表里
- 开放寻址方式
- 应用: 拼写检测,url访问日志排序,字符串包含对比 散列+跳表是redis实现有序集的方式,redis采用双hash,LRU缓存淘汰算法链表+散列表实现的
- 如何设计一个工业级的散列表
- 要求:
- 支持快速增删改查
- 内存空间利用合理,不会浪费
- 性能稳定,极端情况下不会退化到无法接受的地步
- 方案
- 设计一个合适的散列函数
- 定义装载因子的阈值,并且支持动态扩容
- 选择合适的散列冲突解决方式
- 要求:
- 散列函数(哈希函数):
- 从哈希值不能反推原数据
- 对数据很敏感,只要有一个byte不一样,返回的哈希值也不一样
- 散列冲突的概率要很小
- 对于长字符串也能很快的得到结果,效率要高
- 应用
- 安全加密比如MD5和SHA DES AES
- MD5有2^128个哈希值,冲突的概率小于1/2^128
- 唯一标识,图片唯一识别,可以将图片byte转化hash
- 数据校验,如BT中种子信息保存个个节点下载的内容是否被修改过
- 散列函数
- 复杂均衡
- 数据分片
- mapReduce方式任务分配到同一个服务上
- 巨量数据分片,比如1亿张图片如何分开索引
- 如果我们用hash表来存储,就是需要将文件摘要hash后存储
- MD5 128位 16字节,文件路径最大256字节 平均128字节 我们用指针保存数据指针占8个字节一个数据的总 占用量是128+16+8=152,假如一个服务器的内存是2G,hash表的装载因子是0.75,所以单台机器最大存储图片数量 2G*0.75/152约等于1000万,所以一个亿的图片大于需要10台左右这样的机器。
- 分布式存储:一致性哈希,将数据整个哈希分成m个小区间,k台机器上每台机器维护m/k个区间的数据,m远大于k,当有新 机器加入时只要将小部分区间的数据迁移到新的机器便可以,不用改变哈希规则实现扩容。
- 安全加密比如MD5和SHA DES AES
-
二叉树
- 树是非线性数据结构,之前的数组,链表,栈都是线性数据结构
- 树的相关定义
- 节点高度,只当前节点到根节点的最长要经过几个节点
- 节点层级,从1开始
- 节点深度,从0开始
- 最常用的数是二叉树,树只有两个子节点:一个左节点和一个右节点
- 二叉树的类型:
- 满二叉树:最后一层是满的就是满二叉树
- 完全二叉树:倒数第二层是满的,并且最后一层的节点都靠左侧
- 为什么要是完全二叉树,因为内存存储是连续的地址空间,如果用内存存树完全二叉树是最节省内存的方式。
- 二叉树的遍历方式
- 前序:先遍历节点本身
- 中序:中间遍历节点本身
- 后序:后便利了节点本身
- 二叉查找树:二叉查找树是左子叶小于根节点,右子叶大于根节点的树。
- 中序遍历会得到一个顺序的数据
- 二叉查找树的插入,删除,添加都是O(lgn)
- 为什么使用二叉树不用散列表
- 散列表的扩容比较麻烦,虽然查找效率O(1),扩容不方便,并且对于哈希冲突也很难解决,哈希函数的效率有时候也会大于O(lgn)
- 散列是无序的,平衡二叉查找树只需O(n) 可以实现排序
- 散列表的设计比较复杂,要考虑散列函数,扩容,缩容等问题
- 散列表为了减少冲突,必须牺牲一定的存储空间维持,装载因子在一定范围内以减少冲突的可能性
- 红黑二叉树
- 根节点是黑色的
- 叶子结点不能有数据
- 任何相邻的节点不能连续两个是红色
- 每个节点从该节点到子叶节点经过的路径上有相同的黑色节点
- 递归树:一种计算递归算法时间复杂度的方法
-
跳表
在一组数据中,按照一定规则对数据创建层级索引,通过自上至下的索引查询查找数据位置
- 特点
- 二分查找针对数组,为了实现不使用针对数组二分查找,产生了跳跃表
- 跳跃表使用链表
- 有多级索引
- 时间复杂度
- 修改(增删改)时间复杂度 O(lgn)
- 查询时间复杂度O(lgn)
- 空间复杂度
- 空间复杂度根据索引生成方法有关,例子中的大概是O(n)
- n/2+n/4+....+4+2 等比求和 Sn=(a1-anq)/1-q O(n-2) 约等于 O(n)
- 图
- 是描述关系的非线性数据结构
- Trie树
-
递归:f(n)=f(l)+f(r) 利用递推公式 考虑下极限情况即可
-
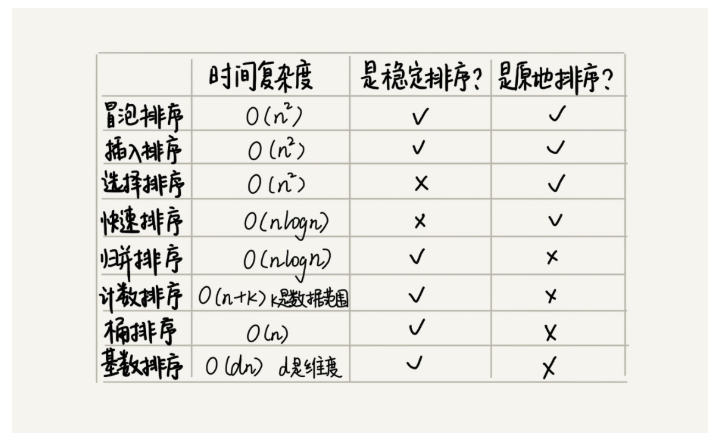
排序:从下面三个方面去衡量算法的好坏
- 最好情况,最坏情况,平均情况时间复杂度
- 时间复杂度的系数,常数,低阶
- 比较次数和移动次数
重要的概念:
- 原地排序:是否借助了额外的空间进行
- 稳定性:排序是否会改变,相同的元素在比较排序的过程中顺序是否会改变
- 比如:2,9,3,4,8,3 排序后是 2,3,3,4,8,9 如果排序前和排序后两个3的前后顺序没有改变,此算法为稳定排序,反之非稳定排序、
- 有序度:有序元素对:a[i] <= a[j], 如果 i < j。
- 满有序度: n*(n-1)/2
- 逆序度:逆序元素对:a[i] > a[j], 如果 i < j。
- 交换次数=满序度-逆序度
归并排序和快速排序思路理解
- 两个排序都是采取分治的思路,归并利用了先分后治,快速排序是先治后分的方式
- 归并排序 空间复杂度 O(n) 时间复杂度 O(nlgn) 并稳定的排序算法 不是原地算法
- 快速排序 空间复杂度 O(1) 时间复杂度 O(nlgn) 并不是稳定的排序算法 是原地算法
总结:如何实现一个通用的排序算法,Glibc 中的 qsort()就是经典案例,在数据量较小的情况下,使用归并排序就行排序,虽然占用空间,但是以空间换时间,在 数据量不大情况下成本并不大,但当数据量达到一定值,换成快速排序,但是快速排序也有缺点,如果使用选分界值,只拿第一个如果频繁遇到最最情况,影响效率所 以可以优化成,三值取中值,或者随机的方式来优化,同时,当数据被分到还有3-4个数据时,可以退化到插入排序,因为当数据量过小时,O(n)和O(lgn)的时间复杂 度已经非常接近了,所以不需要再调用递归了,增加递归的深度。并且快排是递归排序,会产生递归栈太深造成栈溢出,处理这种方式可以采取限制递归深度,或者做 一个调用栈函数,手动实现递归的出栈和入栈。
-
二分搜索:在一组有序的数组中,一半一半的查找时间复杂度O(lgn) 应用要求:
- 只能使用数组的数据结构,要连续的内存地址空间
- 数据量太小不合适 效率和顺序查询差不多
- 数据量太大不合适 占用连续空间大空间不现实
-
哈希算法
-
贪心算法
-
分治算法
-
回溯算法
-
动态规划
-
字符串匹配算法