A set of Python routines to compute the Total Variation (TV) of 2D, 3D and 4D (3D and time) images on CPU & GPU, in application to image denoizing and iterative Computed Tomography (CT) reconstructions. The time-resolved capabilities are useful for dynamic CT or motion artifact corrections. This is the code used in this article.
- Current features
- Installation
- Getting started
- PyTV functions overview
- TV definition
- Comments
- Cite
- License
- Explicit functions to compute the total variation of 2D, 3D, and 4D images.
- Functions return subgradients for easy implementation of (sub)-gradient descent.
- Efficient GPU implementations using PyTorch tensors and convolution kernels.
- Four different spatial discretization schemes are available: upwind, downwind, central, and hybrid (see below).
- Operator-form implementation compatible with primal-dual and proximal formulations (ADMM, Chambolle & Pock algorithm, ...)
First, install PyTorch (version at least 1.5.0) following the guidelines on the official website. Make sure to install the correct version for your setup to enable GPU computations.
Then, the PyTV-4D files can be installed as a package using anaconda:
conda install -c eboigne pytv
PyTV-4D can also be installed manually with (dependencies need to be set properly):
python setup.py install
For a quick installation running the CPU routines only, install numpy and PyTV-4D using anaconda, skipping the PyTorch dependency for PyTV-4D:
conda install numpy && conda install --no-deps -c eboigne pytv
Once installed, you can run some basic tests on CPU and GPU:
import pytv
pytv.run_CPU_tests()
pytv.run_GPU_tests()Note that the tests may fail because of bad rng, so try running it a couple times.
See the details below and the getting started Jupyter notebook.
Below is a simple example to compute the total variation and sub-gradient on CPU and GPU:
import pytv
import numpy as np
Nz, M, N = 20, 4, 100 # 4D Image dimensions. M is for time.
np.random.seed(0)
img = np.random.rand(Nz, M, N, N)
tv1, G1 = pytv.tv_CPU.tv_hybrid(img)
tv2, G2 = pytv.tv_GPU.tv_hybrid(img)
print('TV value from CPU: '+str(tv1))
print('TV value from GPU: '+str(tv2))
print('Sub-gradients from CPU and GPU are equal: '+str(np.prod(np.abs(G1-G2)<1e-5)>0))Output is:
TV value from CPU: 532166.8251801673
TV value from GPU: 532166.8
Sub-gradients from CPU and GPU are equal: True
A simple example of image denoizing using the total variation. The following loss function is minimized:
where is the current image,
is the input noisy image, and
is a regularization parameter.
Because the TV is not everywhere differentiable, the sub-gradient descent method is used to minimize this loss function:
noise_level = 100
nb_it = 300
regularization = 25
step_size = 5e-3 # If step size is too large, loss function may not decrease at every step
np.random.seed(0)
cameraman_truth = pytv.utils.cameraman() # Open the cameraman's grayscale image
cameraman_truth = np.reshape(cameraman_truth, (1,1,)+cameraman_truth.shape)
cameraman_noisy = cameraman_truth + noise_level * np.random.rand(*cameraman_truth.shape) # Add noise
cameraman_estimate = np.copy(cameraman_noisy)
loss_fct_GD = np.zeros([nb_it,])
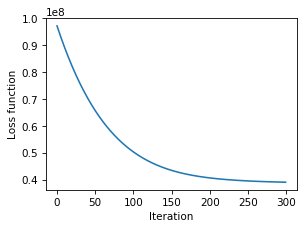
for it in range(nb_it): # A simple sub-gradient descent algorithm for image denoising
tv, G = pytv.tv_GPU.tv_hybrid(cameraman_estimate)
cameraman_estimate += - step_size * ((cameraman_estimate - cameraman_noisy) + regularization * G)
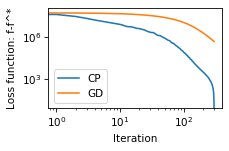
loss_fct_GD[it] = 0.5 * np.sum(np.square(cameraman_estimate - cameraman_noisy)) + regularization * tvBecause the loss function with total variation is non-smooth, it is challenging the achieve sufficient convergence with the gradient descent algorithm. Instead, the primal-dual algorithm from Chambolle and Pock (https://doi.org/10.1007/s10851-010-0251-1) achieves faster convergence. The ADMM algorithm can also be used. To enable easy implementation of such proximal-based algorithm, the calculations of image gradients are available in PyTV-4D. A simple example is presented below in the case of the denoising of the cameraman image:
# A simple version of the Chambolle & Pock algorithm for image denoising
# Ref: Chambolle, Antonin, and Thomas Pock. "A first-order primal-dual algorithm for convex problems with applications to imaging." Journal of mathematical imaging and vision 40.1 (2011): 120-145.
sigma_D = 0.5
sigma_A = 1.0
tau = 1 / (8 + 1)
for it in range(nb_it):
# Dual update
dual_update_fidelity = (dual_update_fidelity + sigma_A * (cameraman_estimate - cameraman_noisy))/(1.0+sigma_A)
D_x = pytv.tv_operators_GPU.D_hybrid(cameraman_estimate)
prox_argument = dual_update_TV + sigma_D * D_x
dual_update_TV = prox_argument / np.maximum(1.0, np.sqrt(np.sum(prox_argument**2, axis = 1)) / regularization)
# Primal update
cameraman_estimate = cameraman_estimate - tau * dual_update_fidelity - tau * pytv.tv_operators_GPU.D_T_hybrid(dual_update_TV)
# Loss function update
loss_fct_CP[it] = 0.5 * np.sum(np.square(cameraman_estimate - cameraman_noisy)) + regularization * pytv.tv_operators_GPU.compute_L21_norm(D_x)PyTV-4D provides the following functions:
- Direct CPU and GPU, for quick (sub)-gradient descent algorithms:
use_GPU = True
import numpy as np
if use_GPU:
import pytv.tv_GPU as tv
else:
import pytv.tv_CPU as tv
Nz, M, N = 20, 4, 100 # 4D Image dimensions. M is for time.
np.random.seed(0)
img = np.random.rand(Nz, M, N, N)
# TV values, and sub-gradient arrays
tv1, G1 = tv.tv_upwind(img)
tv2, G2 = tv.tv_downwind(img)
tv3, G3 = tv.tv_central(img)
tv4, G4 = tv.tv_hybrid(img)- CPU and GPU operators, useful for proximal algorithms:
use_GPU = True
import numpy as np
if use_GPU:
import pytv.tv_operators_GPU as tv
else:
import pytv.tv_operators_CPU as tv
Nz, N = 10, 100 # Image size
M = 2 # Time size
reg_time = 2**(-5) # Time regularization (lambda_t)
img = np.random.rand(Nz, M, N, N)
# Discrete gradient: D_img has size (Nz, Nd, M, N, N) where Nd is the number of difference terms
D_img1 = tv.D_upwind(img, reg_time = reg_time)
D_img2 = tv.D_downwind(img, reg_time = reg_time)
D_img3 = tv.D_central(img, reg_time = reg_time)
D_img4 = tv.D_hybrid(img, reg_time = reg_time)
# Transposed discrete gradient: D_T_D_img has size (Nz, M, N, N)
D_T_D_img1 = tv.D_T_upwind(D_img1, reg_time = reg_time)
D_T_D_img2 = tv.D_T_downwind(D_img2, reg_time = reg_time)
D_T_D_img3 = tv.D_T_central(D_img3, reg_time = reg_time)
D_T_D_img4 = tv.D_T_hybrid(D_img4, reg_time = reg_time)
# TV values: obtained by computing the L2,1 norm of the image gradient D(img)
tv1 = tv.compute_L21_norm(D_img1)
tv2 = tv.compute_L21_norm(D_img2)
tv3 = tv.compute_L21_norm(D_img3)
tv4 = tv.compute_L21_norm(D_img4)- The (Nz, M, N, N) data order is prefered to (M, Nz, N, N) since the CT operations can be decomposed easily along z for parallel beam configurations.
- Time discretization in the operator forms: the discretization scheme used along the time direction is the same as the spatial scheme for each discretization. For the
centralscheme that require M>2, theupwindscheme is used instead for the time discretization for cases with M=2.
Please refer to the following article in your publications if you use PyTV-4D for your research:
@article{boigne2022towards,
author={Boign{\'e}, Emeric and Parkinson, Dilworth Y. and Ihme, Matthias},
journal={{IEEE Transactions on Computational Imaging}},
title={{Towards data-informed motion artifact reduction in quantitative CT using piecewise linear interpolation}},
year={2022},
volume={8},
pages={917-932},
doi={10.1109/TCI.2022.3215096}
}
PyTV-4D is open source under the GPLv3 license.
- Replace mask_static, factor_reg_static with a weight matrix of size Nz x M x N x N that is passed directly onto all functions
- Implement pytv for non-square images
- In 2D, write function to match the
denoise_tv_chambollefunction from scikit-image with a PyTV-4D algorithm.