-
-
Notifications
You must be signed in to change notification settings - Fork 3.5k
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
fix(polyline): stroke bounding rect calculation #8083
Conversation
…1 and 1, and replaced Math.hypot with Math.sqrt
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I don't know if this can generate a bug in case of very small angles
…pathOffset on _setPositionDimension function for polyline
|
Amazing work. |
Great idea! I just committed this change. |
a5a5f06
to
37e4fac
Compare
firefox is crazy enough to calculate this wrong
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
This is excellent work. Thorough and precise.
Most of my comments are related to styling.
I would like to eliminate the use of duplicate code as much as possible and utilize fabric.Point methods such as multiply scalarMultiply making the code more readable.
I will commit visual tests with the examples you have created.
Once I do that it will be easy for you to add more. We should cover all cases and as many edge cases as possible.
I will explain how to run the tests as well.
I would never have figured this out:
In the case of the round, if the angle is less than or equal to 90°, the projection is calculated with two vectors parallel to the X and Y axes. In the case of larger angles, it is calculated using the orthogonals.
Thank you for this awesome contribution!
|
@luizzappa I have created a PR #8087 with tests that is forked from this one. To run tests on fabric:
This will run visual tests on node. Which isn't enough.
And don't hesitate to reach out if it isn't clear enough. |
|
Visual testing has exposed a bug in |
|
https://developer.mozilla.org/en-US/docs/Web/SVG/Attribute/stroke-miterlimit I wonder what is the inner corner of the miter
|
I didn't quite understand what you're comparing to in these tests. Is the percentage of the object that is outside the blue rectangle? Running on node there were no failures. I must be doing something wrong to run in the browser. I cloned fabricjs.com, copied the tests, but they don't show up. |
Would you mind reproducing a buggy case here: https://codesandbox.io/s/fabricjs-project-stroke-working-forked-gem8z9?file=/src/index.js I tried to reproduce but I didn't find the bug. The behavior is different, even the miter limit is at 4, the stroke doesn't become a bevel. I must be missing some parameter. |
|
Forgive me, I forgot a command... To start The tests run and compare the output with an image ref stored in |
|
My bad for the second time! |
Co-authored-by: Shachar <34343793+ShaMan123@users.noreply.github.com>
Co-authored-by: Shachar <34343793+ShaMan123@users.noreply.github.com>
|
@lovegnep you should provide an explanation and a summary, no one should guess why you posted this code here |
|
@ShaMan123 , I'm working on it. It's more difficult than I initially imagined... I got the When I'm going to take this weekend to review some concepts of geometry and calculus, I believe that with the ellipse equation we can take the derivative and find the tangents parallel to the x-axis and y-axis that are candidates for more distant points. |
|
Alright |
|
Just airing some thoughts regarding |
|
If that is the case why don't we intersect the 2 vectors after they are transformed by the plane? |
|
Ok, now I understand why you want to look for the axis tangents. Isn't the bisector orthogonal to the "tip" of the semicircle? Another direction: |
I'm in the flow, give me a few more days, if I can't solve this problem, I focus on refactoring and PR. I will appreciate your help, I have little experience in typescript |
I tried using the point that is in the direction of the bisector before the transformation and then applying the skew (I tried the opposite too), but as the new position of the X depends on the Y height the point is at, it will not necessarily be the solution. Take a look:
I'll take a look, thanks! Mathematically I've already calculated the points that have tangents parallel to the X and Y axes. Now it's translating, I believe I'm close to solving |
|
I adjusted the Just commenting on the solution.. It's a little different than what I initially imagined. The semicircle does not become the segment of an ellipse. The logic behind it is to work with the equation that generates the position of the point after the skew is applied. For example, Limited by the equation (the circle of the Substituting the second equation into the first, taking the derivative and equating to zero to find the maximum/minimum, we find: This is the value of X before applying The problem when So, Then substitute into the |
|
My code is a mess. Tomorrow I will adjust it, and commit to this PR to have a valid version. Then I open a new PR by cloning from the master and work with the new structure in typescript |
|
Outstanding. I will take the advantage and use this PR for learning a bit if you don't mind. Are you looking for a derivative for 2 variables? Is it correct to assume that when Correction Are these functions inverse to each other? |
No, the equation is one-variable. I don't use implicit differentiation. And are inverse: |
|
Got it.
- The furthest X distance from the origin are the maximum/minimun of $f(X_i)$:
+ The furthest Y distance from the origin are the maximum/minimun of $f(X_i)$:??? |
|
I started working on I don't know much about typescript. In the I changed the return to a context: How would I indicate this to typescript? Googling I think it would be something like this: |
|
TS can handle that under the hood. I don't bother adding a return value unless TS is confused about it (some devs like it because it makes the signature strict). What you wrote is fine, a syntax alias to |
|
I referred you to the new guides, right? #8189 Take a look at setting up prettier if you want it seamlessly integrated into the IDE (instead of calling |
The text got a little confusing because of the axes of the graph. In terms of the graph it is the farthest Y, but Y = X after skew X. The graph plots on the X-axis the Xi value (X before skewX), and on the Y-axis the X value after skewX. So the max/min of Perhaps a better wording would be: "The furthest X after skewX distance from the origin are the maximum/minimun of f(Xi)". |
|
I have developed an apatite for your explanations. I love khanacademy |
|
I'll take a look later. What I know of linear algebra is from college (engineering). Depending on the field, there are things that I never studied.. |
|
It works and is correct |
|
@ShaMan123, I'm not finding hypot in util, is it implemented? If not, tell me where I put it There was that precision problem: |
|
Yes |
|
@ShaMan123, As I had to start from scratch from master, I opened a new PR with the branch I worked on. If you think it's better to continue with this PR, I'll close this new one #8344 |
|
I am fine with what you decide. |
|
But isn't a must |
















Related Issues
Proposed changes
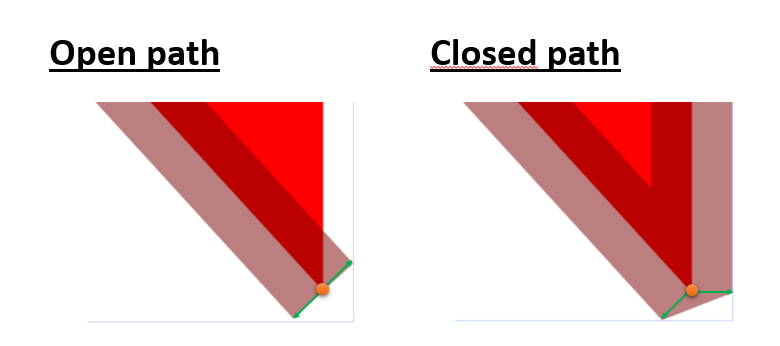
Createdacosfunction infabric.utilto ensure the value is in the range[-1, 1]and thecalcAngleBetweenVectorsfunction is using it. This was causing a bug (see comment on commit bc93beb)IncalcAngleBetweenVectorsfunction, replacesMath.hypot(x, y)withMath.sqrt(x*x + y*y)to ensure equal results in both engines: Firefox and Chrome. (see comment on commit bc93beb)IngetBisectorfunction, checks ifrois close to zero instead of being strictly equal.calcAngleBetweenVectorsfunction, calculate angle between two vector using atan2 instead of dot product. So eliminated the need to check the angle direction ingetBisectorfunction,_setPositionDimensionsfunction in the polyline class to adjust the width/height by the scale in case of uniform stroke.projectStrokeOnPointsfunction to cover all stroke line join cases and also to uniform stroke. This function deserves further comment:In the case of open path, the stroke is rendered differently, so I calculated with the vectors orthogonal to the stroke.
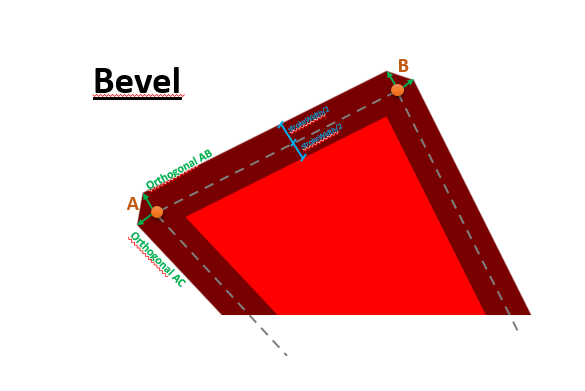
In the case of the bevel, they are the points formed by the orthogonal to the vertex
In the case of the round,
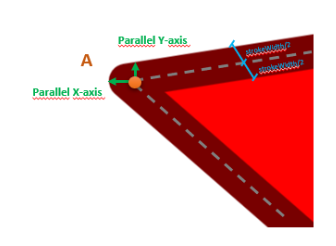
if the angle is less than or equal to 90°,the projection is calculated with two vectors parallel to the X and Y axes.In the case of larger angles, it is calculated using the orthogonals.In the case of the miter, is the same calculation commented here: #8025
For a better view, see this link (you can change the vectors direction by holding the red circles) : https://hypertolosana.github.io/efficient-webgl-stroking/index.html
Screenshots
Working example here: https://codesandbox.io/s/project-stroke-points-with-context-to-trace-b8jc4j?file=/src/index.js
The red dotted vector is the bisector returned by the getBisector function. The green dotted vector is in the opposite direction and is what is used to determine which side to plot the projections. The projections are the colored vectors, one color for each point.
To make debugging easier, you can configure the parameters (stroke line join type, strokeUniform, miterLimit, etc..)
openPath = false and strokeUniform = true