Travelling Salesman Problem

Collaborators. Команда №19

• Мурин Віктор-Микола
• Самойленко Марта
• Кукурік Павло
• Стецишин Вікторія
• Онишкевич Анна
• Швагуляк Катерина

Структура файлів проєкту

• main.py — головний файл проєкту, у якому є усі необхідні функції, які описані нижче.
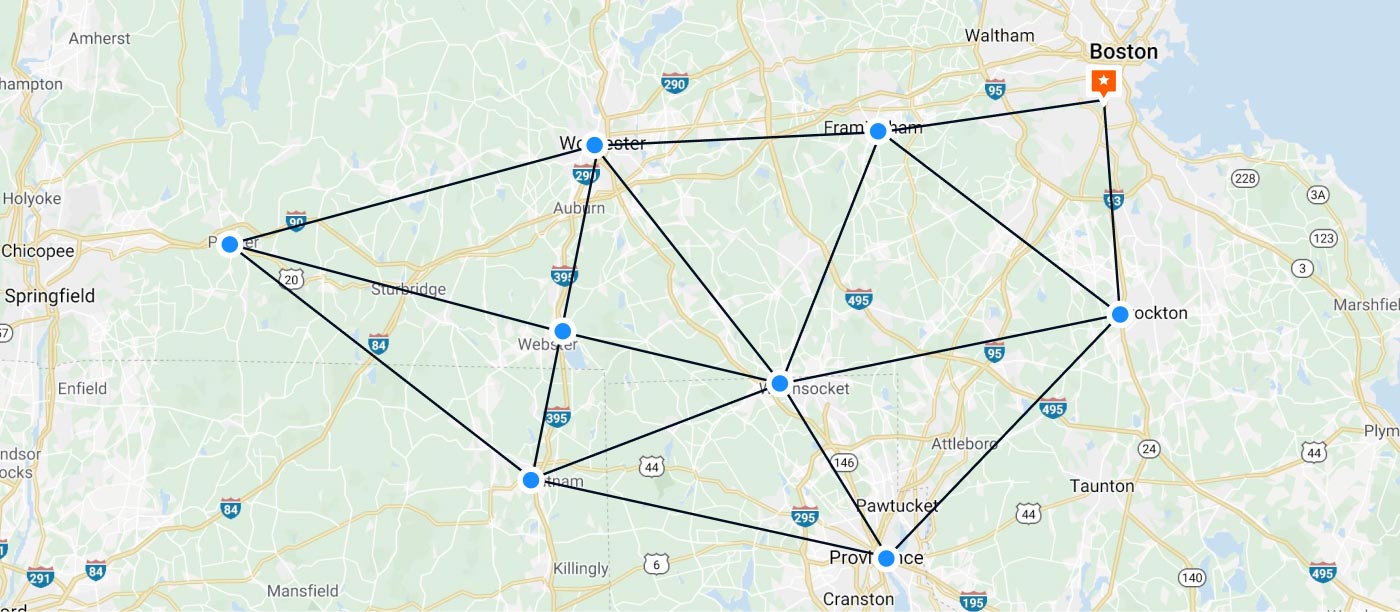
• graph.csv — файл, який репрезентує відстані між містами
• random_matrix.py — допоміжний файл, який генерує випадкову матрицю для тестування
• visualize.py — файл, який створює graph.gv — візуалізацію нашого графу та шляхи різними алгоритмами
• graph.gv — візуалізація графу
• Інші допоміжні файли, не пов'язані з роботою проєкту.

Опис задачі

Комівояжер — мандрівний торговець, який повинен пройти усі міста рівно 1 раз та повернутися у початкове за мінімальну відстань.

Структура файлу main.py

• read_csv(file_path: str) Функція приймає на вхід шлях до файлу (graph.csv), у якому репрезентовано відстань між містами у форматі first,second,distance, що означає, що first місто з'єднане з second, second з'єднане з first, та відстань між ними distance. Якщо шляху між містами не існує, то позначається як infinity.

Для розв'язання задачі ми написали 3 різні алгоритми: точний алгоритм Беллмана-Хелда-Карпа, жадібний алгоритм найближчого сусіда, а також додатковий генетичний алгоритм.

Для алгоритму Беллмана-Хелда-Карпа нам були потрібні допоміжні функції: distance, vertexes_to_bits, binary_without_vertex, dfs, is_connected

• distance(x_city: int, y_city: int, cities_map: CITIES_MAP) Проста функція, яка шукає відстань між двома містами. Більшість функцій у коді чисті, тому багато з них останнім параметром приймають cities_map.

• vertexes_to_bits(combination: Iterable[int]) Для зберігання найкоротшої відстані між першим та останнім містом через combination ми використовуємо dict. Оскільки, combination не є hashable та для пришвидшення (побітові операції є найшвидші), ми переводимо combination у бітове число. Наприклад, комбінація (0, 2, 3, 5) може бути представлене як 101101 = 45

• def binary_without_vertex(vertex: int, binary: int) Видаляє один елемент з комбінації, яка була представлена у побітовій формі. Простіше кажучи, видаляє vertex-ний біт (ставить 0). Наприклад, комбінація (0, 2, 3, 5) у побітовій формі = 101101 = 45. Якщо ми хочемо видалити 2 з комбінації, то слід другий біт зробити 0. Вийде (0, 3, 5) = 101001 = 41.

• dfs(graph: CITIES_MAP) Функція, яка робить пошук у глибину по графу. Потрібно для наступної функції.

• is_connected(graph: CITIES_MAP) Перевіряє, чи є граф зв'язний. Використовує dfs та намагається пройти по всьому дереву. Якщо |graph| == |dfs|, то граф зв'язний.

Алгоритм Беллмана-Хелда-Карпа динамічного програмування (exact_tsp)

Для розв'язку цієї задачі у точний спосіб є 2 підходи: метод грубої сили (перебір усіх можливих варіантів) та алгоритм Хелда-Карпа. Складність першого алгоритму O=n!, що занадто довгий. У той ж час другий має складність O=n²2ⁿ, що набагато швидше.

Суть алгоритму: вибирається одне місто початковим. Немає різниці яке, адже в кінцевому результаті вийде замкнене коло. Визначаємо відстань між першим та k-им містом та зберігаємо у dict. Потім проходимо по усіх комбінаціях розміром 2...n (n — кількість міст) та визначаємо найкоротший шлях між першим та k-им містом через комбінацію. Для цього можемо подивитися у збережений dict, щоб не рахувати увесь шлях заново. В кінцевому результаті отримуємо останній елемент з найкоротшого шляху. Для реконструкції шляху, заново проходимося по dict у зворотному порядку. Це і є динамічне програмування у такому випадку.

Через те, що dict розростається до великих розмірів, space complexity = n*2ⁿ.

Жадібний алгоритм найближчого сусіда (nna)

Алгоритм, починає з першого міста та завжди шукає найближче місто та йде до нього. Алгоритм не точним та пропонує лише приблизний розв'язок, проте є дуже швидким у порівняні з точним. Складність оцінюється O=n².

Додаткове: генетичний алгоритм (genetic)

Алгоритм Беллмана-Хелда-Карпа та алгоритм найближчого сусіда мають очевидні проблеми: перший працює надто довго для n > 20, другий має надто малу точність. Для цього ми реалізували третій алгоритм — генетичний.

Суть алгоритму проста: для початку ми беремо абсолютно випадковий шлях та шукаємо його довжину. Потім n разів міняємо місцями 2 випадкові його елементи та дивимося, чи новий шлях є менший за минулий. Повторюємо ще n-1 разів. Також, щоб оптимізувати алгоритм та зменшити кількість ітерацій n, ми робимо одночасно k незалежних шляхів. Потім серед них вибирається найменший.

Додаткове: візуалізація

У файлі visualize.py створюється візуалізація графу, який записаний у файлі graph.csv, потім викликається усі три алгоритми, які шукають свої найкоротші шляхи та це все записується у файл graph.gv, який потім легко візуалізувати на сайті https://dreampuf.github.io/GraphvizOnline/

Запуск коду

Усі функції пошуку є у файлі main.py. Приклади запуску:

• exact_tsp( read_csv('graph.csv') )
• nna( read_csv('graph.csv') )
• genetic( read_csv('graph.csv') ). Також можна погратися з 2 та 3 аргументами — кількістю шляхів та мутацій

Також можливий такий варіант: exact_tsp( [[0, 2, 9, 10], [1, 0, 6, 4], [15, 7, 0, 8], [6, 3, 12, 0]] )