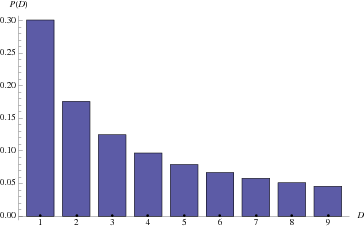
Benford's law Benford's Law is an observation about the leading digits of the numbers found in real-world data sets. Intuitively, one might expect that the leading digits of these numbers would be uniformly distributed, so that each of the digits from 1 to 9 are equally likely to appear. In fact, it is often the case that 1 occurs more frequently than 2, 2 more frequently than 3, and so on. This observation is a simplified version of Benford's law. More precisely, the law gives a prediction of frequency of leading digits using base-10 logarithms that predicts specific frequencies which decrease as the digits increase from 1 to 9.
This phenomenon occurs generally in many different instances of real-world data. It becomes more pronounced and more likely when more data is combined together from different sources. Not every data set satisfies Benford's law, and it is surprisingly difficult to explain the law's occurrence in the data sets it does describe, but nevertheless it does occur consistently in well-understood circumstances. Scientists have even begun to use versions of the law to detect potential fraud in published data (tax returns, election results) that are expected to satisfy the law. This is a simple graph showing numbers from 1 to 9 and their respective probability percentage of oocurrence
- A browser preferrably use Google Chrome
- Python3
- pip install flask
- pip install werkzeug
- Access the online app at: https://okro.herokuapp.com/
- Or -Clone this repository: git clone https://github.com/idawud/Okro/
- Launch Server using the python IDE preferrably Pycharm
- run app.py file
through your terminal or command prompt run: python app.py
- On a local server
enter 0.0.0.0 in your browsers address bar
- Upload your CSV file
click on submit to generate Results
Ismail Dawud Ibrahim ismaildawud96@gmail.com
Prince Alfred Gyan princealfredgyan@gmail.com
Franklin Wae Luther franklinluther3@gmail.com
Francis Billa francis.billa.fb@gmail.com