Tools for working with recursive data structures in a concise, stack safe, and performant manner.
This crate provides abstractions for separating the machinery of recursion from the logic of recursion. This is similar to how iterators separate the machinery of iteration from the logic of iteration, allowing us to go from this:
let mut n = 0;
while n < prices.len() {
print!("{}", prices[n]);
n += 1;
}to this:
for n in prices.iter() {
print!("{}", n)
}This second example is less verbose, has less boilerplate, and is generally nicer to work with. This crate aims to provide similar tools for working with recursive data structures.
For these examples, we will be using a simple recursive data structure - an expression language that supports a few mathematical operations.
pub enum Expr {
Add(Box<Expr>, Box<Expr>),
Sub(Box<Expr>, Box<Expr>),
Mul(Box<Expr>, Box<Expr>),
LiteralInt(i64),
}For working with this Expr type we'll define a frame type ExprFrame<A>.
It's exactly the same as Expr, except the recursive self-reference Box<Self> is replaced with A.
This may be a bit confusing at first, but this idiom unlocks a lot of potential (expressiveness, stack safety, etc).
You can think of ExprFrame<A> as representing a single stack frame in a recursive algorithm.
pub enum ExprFrame<A> {
Add(A, A),
Sub(A, A),
Mul(A, A),
LiteralInt(i64),
}Now all we need is some mechanical boilerplate: [MappableFrame] for ExprFrame and [Expandable] and [Collapsible] for Expr.
I'll elide that for now, but you can read the documentation for the above traits to learn what they do and how to implement them.
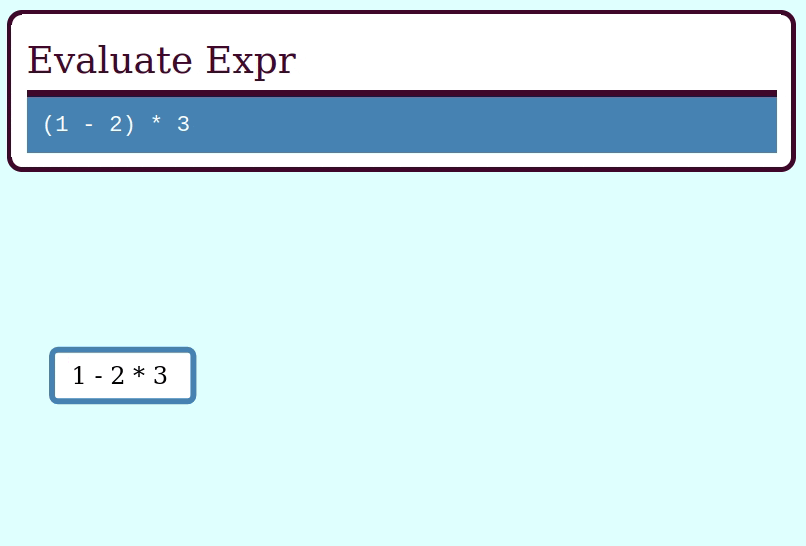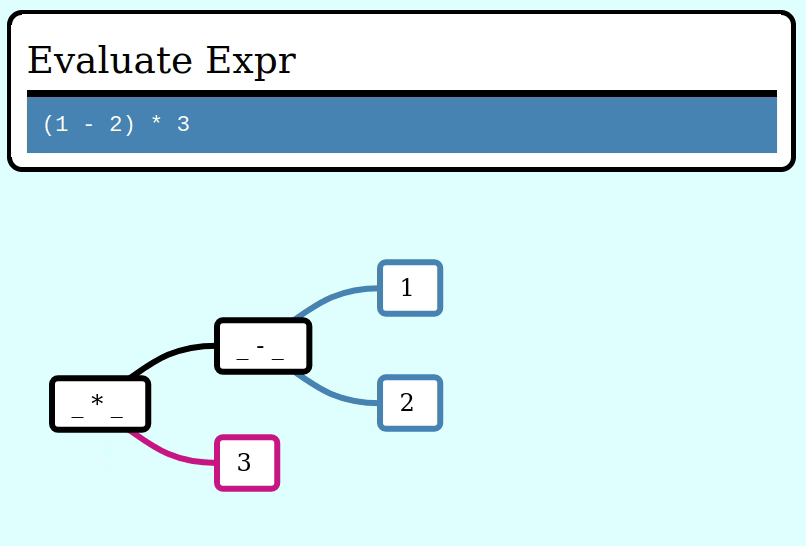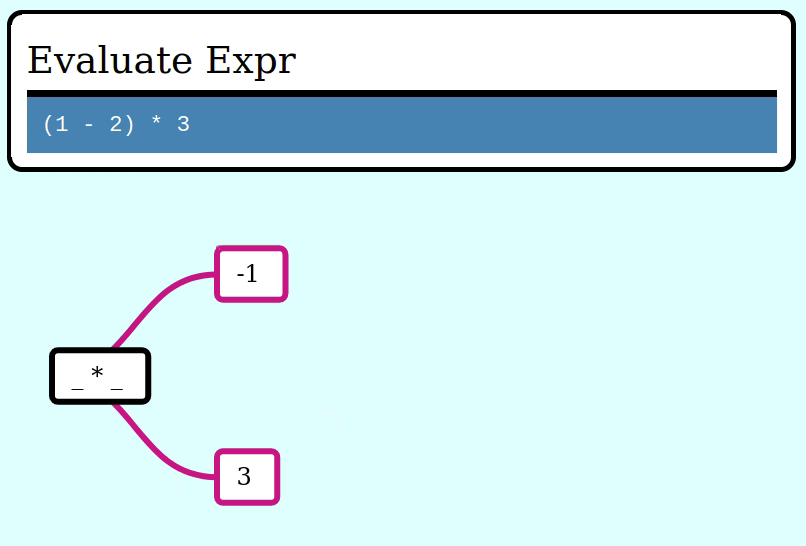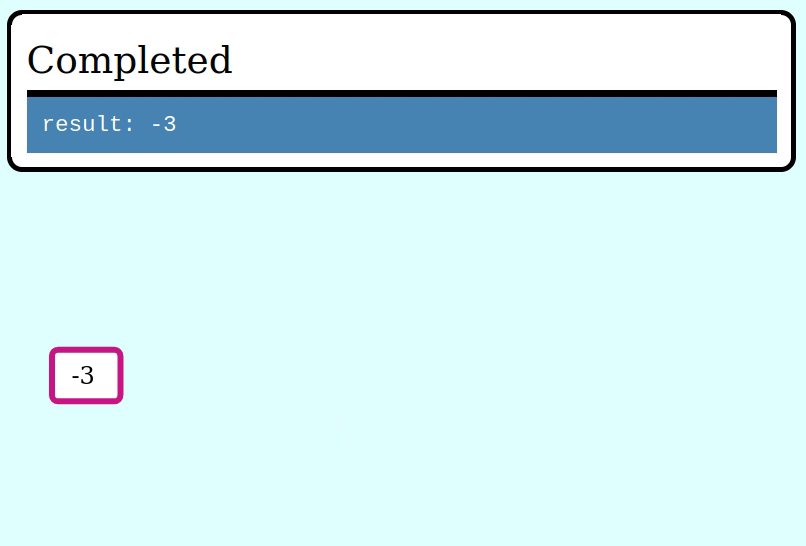
Here's how to evaluate an Expr using this idiom, by collapsing it frame by frame via a function ExprFrame<i64> -> i64:
fn eval(e: &Expr) -> i64 {
e.collapse_frames(|frame| match frame {
ExprFrame::Add(a, b) => a + b,
ExprFrame::Sub(a, b) => a - b,
ExprFrame::Mul(a, b) => a * b,
ExprFrame::LiteralInt(x) => x,
})
}
let expr = multiply(subtract(literal(1), literal(2)), literal(3));
assert_eq!(eval(&expr), -3);Here's a GIF visualizing the operation of collapse_frames:
At this point, you may have noticed that We've ommited division, which is a fallible operation
because division by 0 is undefined. Many real world algorithms also have to handle failible operations,
such as this. That's why this crate also provides tools for collapsing and expanding recursive data
structures using fallible functions, like (in this case) ExprFrame<i64> -> Result<i64, Err>.
fn try_eval(e: &Expr) -> Result<i64, &str> {
e.try_collapse_frames(|frame| match frame {
ExprFrame::Add(a, b) => Ok(a + b),
ExprFrame::Sub(a, b) => Ok(a - b),
ExprFrame::Mul(a, b) => Ok(a * b),
ExprFrame::Div(a, b) =>
if b == 0 { Err("cannot divide by zero")} else {Ok(a / b)},
ExprFrame::LiteralInt(x) => Ok(x),
})
}
let valid_expr = multiply(subtract(literal(1), literal(2)), literal(3));
let invalid_expr = divide(literal(2), literal(0));
assert_eq!(try_eval(&valid_expr), Ok(-3));
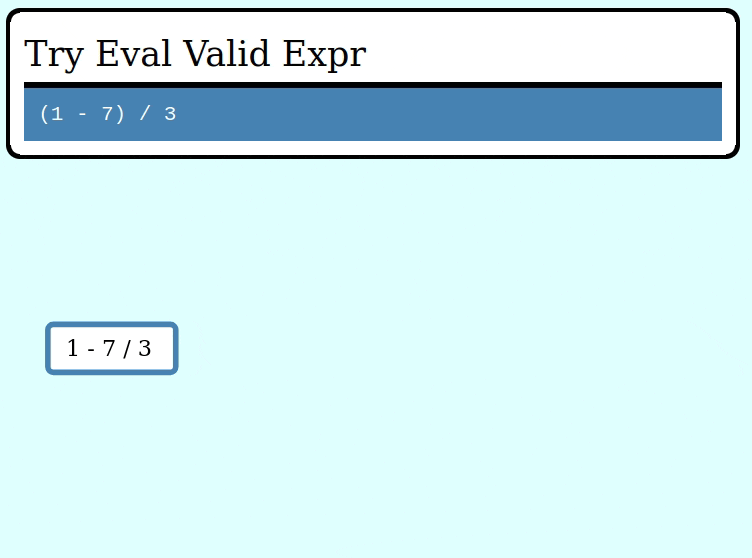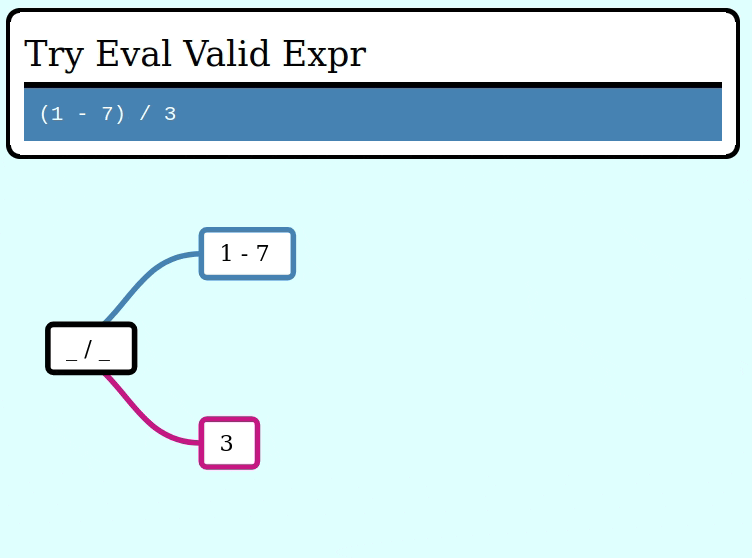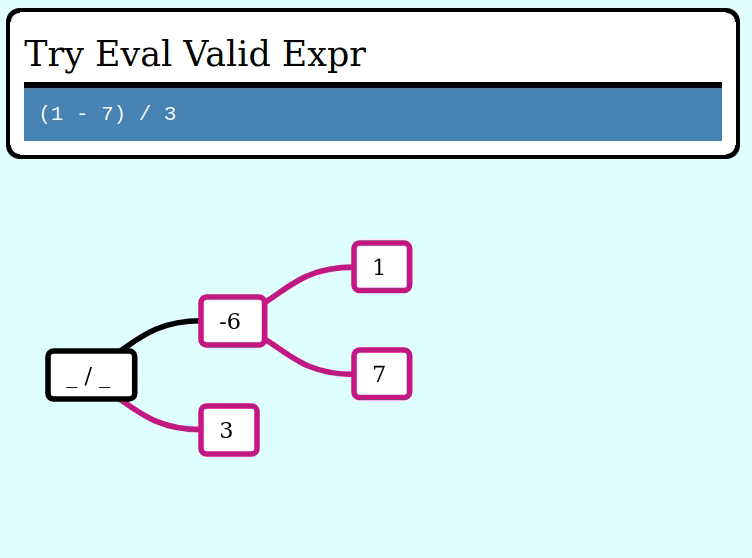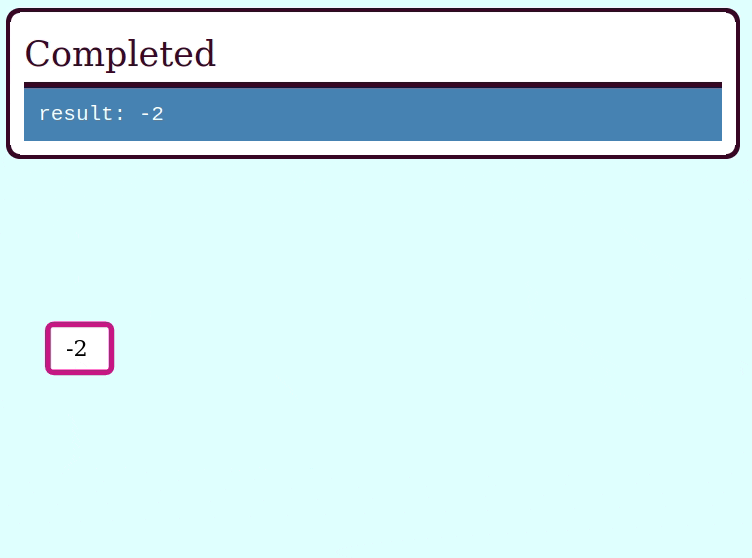
assert_eq!(try_eval(&invalid_expr), Err("cannot divide by zero"));Here's a GIF visualizing the operation of try_collapse_frames for valid_expr:
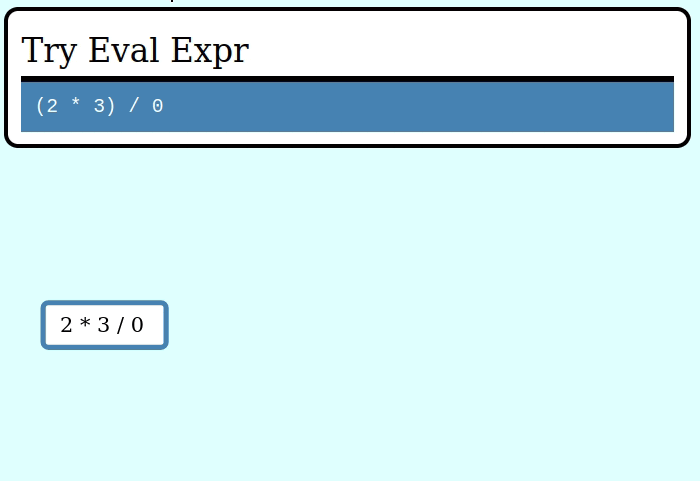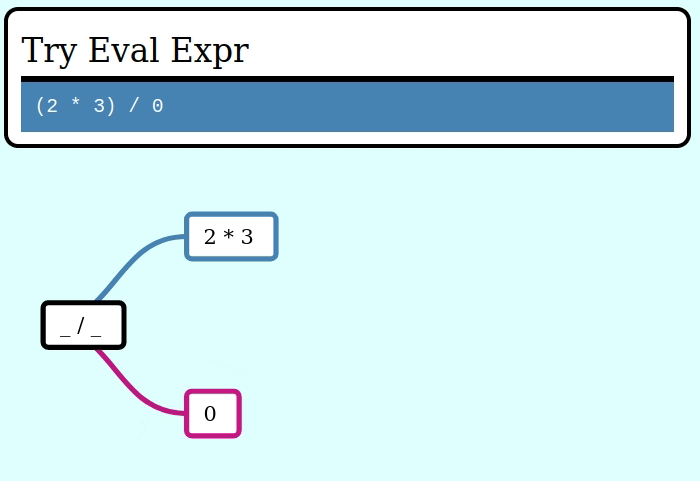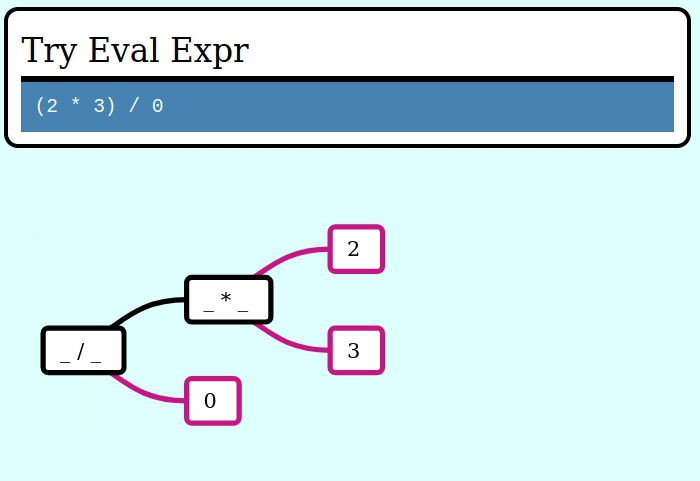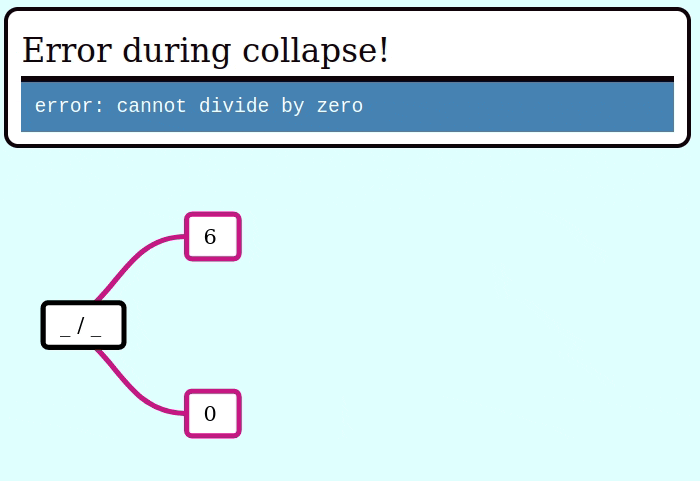
And here's a GIF visualizing the operation of try_collapse_frames for invalid_expr:
Here's an example showing how to expand a simple Expr from a seed value
fn build_expr(depth: usize) -> Expr {
Expr::expand_frames(depth, |depth| {
if depth > 0 {
ExprFrame::Add(depth - 1, depth - 1)
} else {
ExprFrame::LiteralInt(1)
}
})
}
let expected = add(add(literal(1), literal(1)), add(literal(1), literal(1)));
assert_eq!(expected, build_expr(2));Here's a GIF visualizing the operation of `expand_frames``:
All GIFs in this documentation were generated via tooling in my recursion-visualize crate, via examples/expr.rs.
If you're familiar with Haskell, you may have noticed that this crate makes heavy use of recursion schemes idioms.
I've named the traits used with an eye towards readability for users unfamiliar with those idioms, but feel free to
read [MappableFrame] as Functor and [Expandable]/[Collapsible] as Corecursive/Recursive. If you're not
familiar with these idioms, there's a great blog post series here that explains the various concepts involved.
License: MIT OR Apache-2.0