Overview

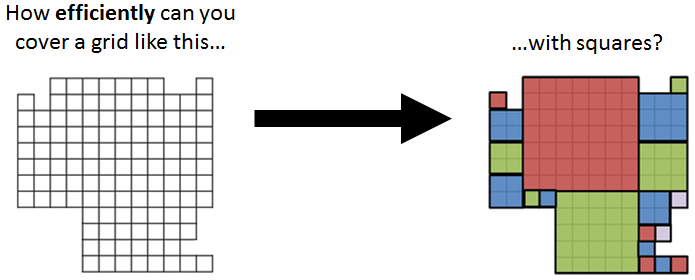
This is Jason Ansel's entry in the Cimpress Tech Challenge from May 2015. It made it into the finals and received an honorary mention.

This entry is an evolutionary algorithm with a non-obvious representation, crossover operator, and mutation operator. The code has also been heavily optimized to enable running a large number of generations in the ten seconds allotted to solve each problem instance. Many independent copies of the evolutionary algorithm are run in parallel and the best result is submitted.

Representation

For a representation, I wanted something that would be easier to work than the list of (X, Y, Size) squares used as the submission format. The goals for designing the representation were:

• It should cover only valid solutions. (No correctness checking required in mutation / crossover)
• All possible solutions should be representable. (Over-approximation of search space.)
• Biased towards solutions using fewer squares.
• Simple.

The representation is a permutation of all tiles in the puzzle with a scoring function (a.k.a. fitness function) that maps any possible permutation to a correct puzzle solution. This scoring function operates by iterating over the permutation in order. For each tile, if the tile is not yet filled, it draws a new square starting at that tile and expanding down and to the right to fill all currently empty space. One way to think of this scoring function is as a greedy algorithm for this problem, modified just enough so that it is able to generate every possible solution.

Mutation

The mutation operator is applied to every new member of the population as it is created. To find a mutation operator, I experimentally tried dozens of possible candidates. The final choice does two things:

• Selects one random tile and shifts to to the front of the permutation.
• Selects another random tile and shifts to to the back of the permutation.

Shifting to the front effectively forces a square to be drawn at a given tile, while shifting to the back suppresses a square from being drawn at that tile.

Crossover

The crossover operator is applied to create half of the new members of the population. The other half of the new members are created by copying from a single parent. In both cases mutation is applied. This crossover operator was found after experimenting with dozens of possible algorithms.

Crossover works as follows:

• Randomly select two parents from the population.
• Randomly draw an angled line across the puzzle grid.
• Output all points that are above the line from the first parent, preserving their order.
• Output all points that are below the line from the second parent, preserving their order.

Selection

The population is composed of the top K permutations found so far, recomputed after each generation. Parents are selected uniform randomly from the population.

Initial Population

The initial population is seeded with heuristics that sort the population by differently weighted combinations of X, Y, and N, where N is the maximum possible sized square that could be drawn from the point without hitting walls in the puzzle.

Empirically this initial population improves convergence time compared to a random starting point, but has little effect on the quality the final results.

Optimizations

The implementation contains many optimizations that improve performance and results, including:

• The representation excludes all tiles from which only a 1x1 square could ever be drawn.
• The scoring function will refuse to draw 1x1 squares in its initial pass.
• A second pass in the scoring function draws 1x1 squares on any empty tiles. This bias against 1x1 squares makes some solutions non-representable, but those solutions are provability non-optimal because shrinking a square to add only 1x1 tiles will never improve a score.
• Points are packed into a single uint32, where 16 bits are used for each part of the coordinate.
• For performance, crossover and mutation (and copy and mutation) are combined into a single optimized functions which do only a single pass over the list.
• Selection is done using a modified version of partition from quicksort which selects the top K members of the population without fully sorting the population.
• Memory is managed carefully, such that no allocations are done in the main loop.
• Numba is used to JIT compile python with LLVM. This provides a large performance boost, but requires using a restricted subset of python in the JIT compiled code.
• The scoring function used in the main loop 1) only counts the number of squares, does not generate them 2) avoids the second pass by subtracting the total tiles covered from the total tiles 3) is manually loop unrolled for performance.
• Drawing the random line in the crossover is approximated with integer math rather than using slower floating point math.

Dependencies

This code depends on Miniconda (Python 2.7) with the packages Numba and Twisted installed. On GNU/Linux, setup can be accomplished with the following commands:

wget https://repo.continuum.io/miniconda/Miniconda-latest-Linux-x86_64.sh
bash Miniconda-latest-Linux-x86_64.sh -b
~/miniconda/bin/conda install -y numba twisted

Example Usage

To run a standalone instance of the solver on a local file:

~/miniconda/bin/python gridea.py --file example_puzzle.json

A complete list of options are available by running gridea.py --help.

Parallel and Distributed Processing

Since the evolutionary algorithm is a stochastic process, running many independent copies and taking the best improves expected results. This code contains a simple broadcast protocol that can be used to create clusters of solvers.

To create a cluster of 12 solvers on three machines:

node1$  ~/miniconda/bin/python gridea.py --workers=4
node2$  ~/miniconda/bin/python gridea.py --workers=4 --link=node1:8099
node3$  ~/miniconda/bin/python gridea.py --workers=4 --link=node1:8099

Then, to use this cluster of 12 processes with a local puzzle file:

node1$ ~/miniconda/bin/python run.py --file=example_puzzle.json

Or, to interact with the challenge API server:

node1$ ~/miniconda/bin/python run.py --key=... --mode=trial -n400

A complete list of options are available by running run.py --help.

Code

• gridea.py: The main definition of the evolutionary algorithm
• scoring.py: Expand the permutation representation to full list of boxes or count the number of boxes that would be required
• initialize.py: Heuristics used to form the initial population of the evolutionary algorithm
• network.py: Broadcast protocol used to build a distributed cluster of solver processes
• run.py: Interact with the challenge API server and submit solutions
• utils.py: Some general helper functions