- IMage Euclidean Distance (IMED)
The IMED is the Euclidean distance (ED) applied to a transformed version of an image or n-dimensional volume that has image-like correlation along axes. It solves some of the shortcommings of using the pixel-wise Euclidean distance in classification or regression problems. Small displacements do not have as large an impact on the similarity measure when IMED is used over the ED.
Below, two binary 2D images are displayed, each in two versions. One image has white pixels that are slightly displaced compared to the other. With the original 'sharper' images, the ED between these two images is large, since ED does not take into account any surroundings of each pixel. This is despite the obvious similarity to the naked eye. The 'blurred' versions are standardizing transformed (ST) with a certain Gaussian filter. The displacement is not penalized as harshly by the ED on these images.
This is the IMED: The Euclidean distance evaluated on ST-images.
This package contains efficient python implementations of the IMED (distance, transforms) and adds robust inverse transforms for first-ever utility in regression problems e.g. spatio-temporal forecasting.
imed.legacy contains legacy transforms, i.e. slower or less useful versions of the IMED, for historical reasons.
Implementations are based on and extend the work of On the translation‑invariance of image distance metric [1].
The ST is a convolution-based transformation. This package therefore implements the transforms in frequency space. Fourier Transform (FFT) and Discrete Cosine Transform (DCT) methods are available, with slightly different edge effects as a result. The DCT is recommended for natural images since it performs symmetric convolution. The frequency-based methods allow parallelization and distributed computations if needed.
In the future, an even more efficient finite-support version of the transforms will be added (see this issue)
In On the Euclidean distance of images [2] the IMED was presented for ED-compatible classification and clustering methods. These only require a 'forward' transform to perform computations on the altered data set or images.
Methods include: Any classification method applying an 'L2 loss function', Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), SVMs, Neural Networks, k-nearest neighbours, clustering methods.
This package extends the IMED to use in regression problems. These problems require the default forward ST to be performed on the dataset. This is used an input in a predictor model that uses L2 loss (traditionally), and the predictions are 'blurred' like the augmented dataset. These predictions may not be satisfactory.
The inverse ST is used in this case, and called like:
from imed import transform
# forward transform
img_ST = transform(img,sigma=2, eps=1e-2, inv=False)
# any L2 loss prediction method with image output
img_predicted_ST = predict(img_ST)
# sharpen prediction using backwards/inverse ST
img_predicted = transform(img_predicted_ST, sigma=2, eps=1e-2, inv=True)The eps parameter is crucial in both the forward and backwards pass and must have the same value small, positive value in the two. Problems for which the inverse transform is not needed do not require eps to be non-zero. eps allows robust deconvolution. If it is not used, the inverse predictions may completely unusable due to noise amplification in inverse filtering.
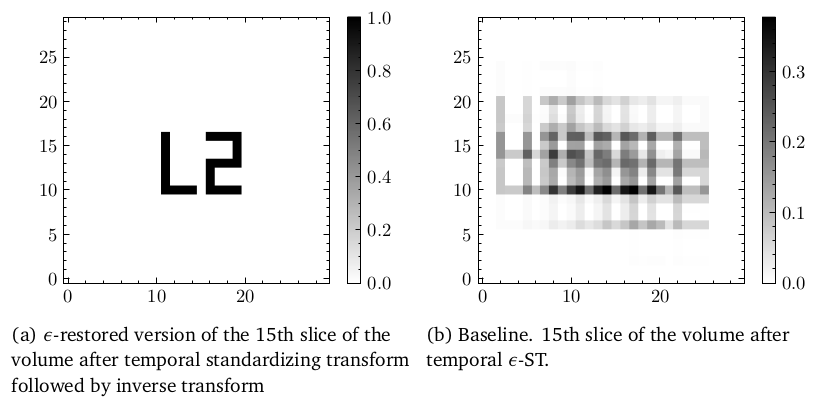
Below is an example of restoring a forward ST transformed sequence (right) to one that is almost identical to the original image in the sequence (left). The forward transform had non-zero sigma only along the temporal axis in which the 'L2' motif moved around along the spatial axes.
The standardizing transform is a convolution-based method. It can therefore is sensible to perform it along any axes of correlation, and this is implemented by imed.transform.
In some problems, e.g. spatio-temporal ones, it is often advisable to use different valStandardizingues of the Gaussian 'blurring parameter' sigma along some axes (time vs. spatial axes). For n-dimensional volumes for which the same value e.g. sigma = 1 must not be used, an array-like sigma can be passed with axis-per-axis values. sigma = [0., 1., 1.] may be proper for a 3D data volume (T, M, N) of T images. sigma = [0.5., 1., 1.] may be used for 'blurring' along the temporal axis, too.
sigma: (int or array-like) Gaussian 'blurring' parameter (real-space interpretation). If int: ST uses samesigmavalue along all axes. If 0: ST is skipped along that axis (array-like argument). Each value ofsigmadefines a new IMED loss function. IMED loss values should not be compared using different values of sigma.inv: (bool.) Whether to perform the forward (False) transform or backwards (True). Other parameters should be matched when an inverse transform is required following the forward ST.epsShould only be used when an inverse transform is required. In these case, use the same, small value ofepsin the forward and backwards transforms.
Install the latest release from pypi:
pip install imed
The standardizing transform as pictured in the introduction is easily computed for a single image, image sequence or general data volume. The easiest way to get started is to run:
imed.transform(volume, sigma, inv=False, eps=1e-2, method="DCT")The function outputs a volume with the same shape that has been transformed according to the selected arguments.
In regression problems the IMED is utilized as a loss function by transforming the data using a forward ST-transform with e.g. eps=1e-2 (robustly). The prediction method is then applied to the transformed data, and outputs such 'blurred' predictions.
When these are achived, the predictions can be 'unblurred' by performing the inverse transform:
imed.transform(volume, sigma, inv=True, eps=1e-2, method="DCT")When one expects that an inverse transform of 'blurred' predictions will be necessary, the same values of eps should be chosen in the forward and backwards standardizing transforms! eps = 0 should be chosen when an inverse transform is not needed.
To compute the IMED score between two volumes, one may compute:
imed.distance(volume1, volume2, sigma=1)The two data volumes must have identical shape. It may be a single image, a collection of images, or a high-dimensional volume. See the docstring for more details. The function allows the computation of a single volume-wide similarity score, or an array of similarity scores to be computed.
The function first performs the standardizing transform on the data volumes and compares the transformed volumes using the ED afterwards.
The IMED methods are implemented using the scipy.fft module.
By chopping up the transforms into smaller chunks, SciPy supports parallelization by specifying the workers environment variable:
from scipy import fft
with fft.set_workers(-1):
imgs_ST = imed.transform(volume, sigma)When the number of workers is set to a negative integer (like above), the number of workers is set to os.cpu_count().
SciPy also supports computations using another backend. For example, we can use pyFFTW as backend like so:
from scipy import fft
import pyfftw
with fft.set_backend(pyfftw.interfaces.scipy_fft):
#faster if we enable cache using pyfftw
pyfftw.interfaces.cache.enable()
# perform standardizing transform using frequency method of your choice
imgs_ST = imed.transform(volume, sigma)