Skip to content
This repository has been archived by the owner on Sep 14, 2023. It is now read-only.
/ athena Public archive

Translates Metis ATP proofs to the Agda code

License

MIT license
6 stars 2 forks Branches Tags Activity
Star
Notifications You must be signed in to change notification settings

jonaprieto/athena

BranchesTags

Repository files navigation

Proof-Reconstruction in Type Theory for Propositional Logic Build Status DOI

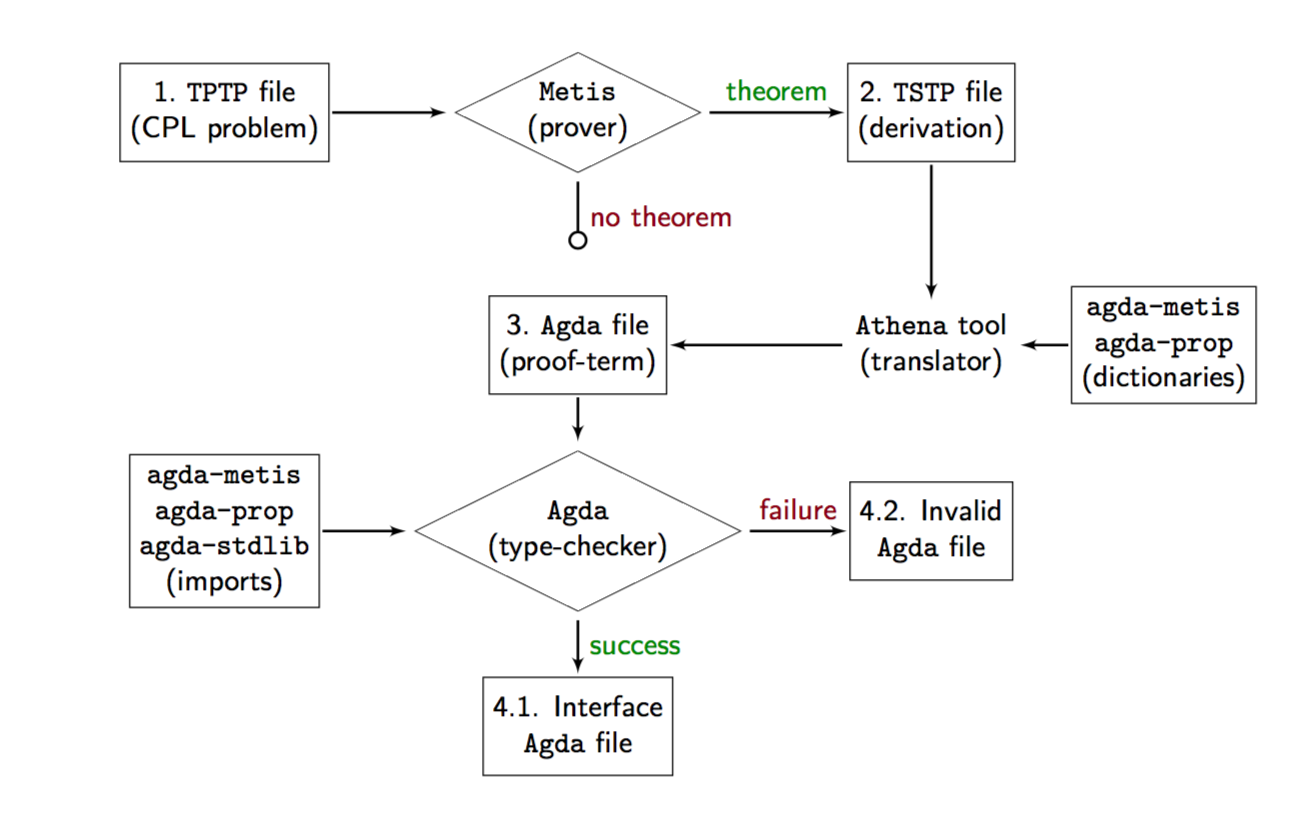
Athena is a Haskell proof-reconstruction tool. This tool is able to translate TSTP derivations generated by Metis to Agda proof-terms. To verify such derivations generated automatically by Metis, we type-check the proof-terms generated by Athena using the proof-assistant Agda. In the following diagram, we present a work-flow using Athena during the proof-reconstruction task.

diagram

A description of this approach to reconstruct propositional derivations generated by Metis is available at:

Table of Contents

Installing the Athena Tool

This tool is written in Haskell and it was tested with

To install Athena, the package manager cabal is required as well, version ≥2.2.0.0. Athena was tested with

Now, to install Athena just download this repository by running the following command:

  $ git clone https://github.com/jonaprieto/athena.git
  $ cd athena

To install Athena from the command line run the following:

  $ make install

The proofs generated using this tool were tested with

Using the Agda libraries listed below:

There is a possibility to install the Agda libraries (agda-prop, agda-metis and the Agda standard library) run the following command:

  $ make install-libraries

Follow the instructions given by the command, the libraries will be installed in the lib folder. If you know about these .agda files, you probably want to specify in the .agda/defaults and .agda/libraries files the paths of the libraries necessary for proof-reconstruction.

Installing the Metis Prover

Athena only supports reconstruction for the Metis prover, we tested with:

To install this tool run the following command and follow the instructions.

  $ make metis

We have an alternative way to use this prover and many others. Its our client for the Systems on the TPTP World:

To install this tool run the following command:

  $ make online-atps
  $ online-atps --version
  Online-atps version 0.1.3

Testing

We have included a test-suite of at least eighty theorems from Prop-Pack TPTP Collection:

$ make install
$ make install-libraries
$ make problems
$ make check

To just generate the Agda files run the command:

$ make reconsruct

Example

TPTP problem

Let us consider the following theorem problem No. 13 in Disjunction Section in Prop-Pack:

(p \Rightarrow q) \wedge (q \Rightarrow p)\ \vdash\ (p \vee q) \Rightarrow (p \wedge q)

This problem can be encode in TPTP syntax (file problem.tptp) as follows:

  $ cat problem.tptp
  fof(premise, axiom, (p => q) & (q => p)).
  fof(goal, conjecture, (p | q) => (p & q)).

Metis derivation

To obtain the Metis derivation of the TPTP problem showed above, make sure your Metis version is supported by running the following command. Recall we support the version 2.4.+

  $ metis --version

To generate the TSTP derivation of problem.tptp run the following command:

  $ metis --show proof problem.tptp > problem.tstp
  $ cat problem.tstp
  ...
  fof(premise, axiom, ((p => q) & (q => p))).
  fof(goal, conjecture, ((p | q) => (p & q))).
  fof(subgoal_0, plain, ((p | q) => p), inference(strip, [], [goal])).
  fof(subgoal_1, plain, (((p | q) & p) => q), inference(strip, [], [goal])).
  fof(negate_0_0, plain, (~ ((p | q) => p)),
      inference(negate, [], [subgoal_0])).
  ...

If you are using the Online-ATPs tool run the following command:

  $ online-atps --atp=metis problem.tptp  > problem.tstp

Using our customized TSTP syntax, the above Metis derivation looks like:

  fof(premise, axiom, (p ⊃ q) ∧ (q ⊃ p)).
  fof(goal, conjecture, (p ∨ q) ⊃ (p ∧ q)).
  fof(s₀, (p ∨ q) ⊃ p, inf(strip, goal)).
  fof(s₁, ((p ∨ q) ∧ p) ⊃ q, inf(strip, goal)).
  fof(neg₀, ¬ ((p ∨ q) ⊃ p), inf(negate, s₀)).
  fof(n₀₀, (¬ p ∨ q) ∧ (¬ q ∨ p), inf(canonicalize, premise)).
  fof(n₀₁, ¬ q ∨ p, inf(conjunct, n₀₀)).
  fof(n₀₂, ¬ p ∧ (p ∨ q), inf(canonicalize, neg₀)).
  fof(n₀₃, p ∨ q, inf(conjunct, n₀₂)).
  fof(n₀₄, ¬ p, inf(conjunct, n₀₂)).
  fof(n₀₅, q, inf(simplify, [n₀₃, n₀₄])).
  cnf(r₀₀, ¬ q ∨ p, inf(canonicalize, n₀₁)).
  cnf(r₀₁, q, inf(canonicalize, n₀₅)).
  cnf(r₀₂, p, inf(resolve, q, [r₀₁, r₀₀])).
  cnf(r₀₃, ¬ p, inf(canonicalize, n₀₄)).
  cnf(r₀₄, ⊥, inf(resolve, p, [r₀₂, r₀₃])).
  fof(neg₁, ¬ ((p ∨ q) ∧ p) ⊃ q), inf(negate, s₁)).
  fof(n₁₀, ¬ q ∧ p ∧ (p ∨ q), inf(canonicalize, neg₁)).
  fof(n₁₁, (¬ p ∨ q) ∧ (¬ q ∨ p), inf(canonicalize, premise)).
  fof(n₁₂, ¬ p ∨ q, inf(conjunct, n₁₁)).
  fof(n₁₃, ⊥, inf(simplify, [n₁₀, n₁₂])).
  cnf(r₁₀, ⊥, inf(canonicalize, n₁₃)).

Generating the Agda proof-term

To obtain the Agda proof-term of the Metis derivation run the following command:

  $ athena problem.tstp

Athena will create the Agda file of the solution. The Agda file should look like this one:

  $ cat problem.agda
  ------------------------------------------------------------------------------
  -- File automatically generated by Athena version 0.2-xxxxx
  -- TSTP file: problem.tstp.
  ------------------------------------------------------------------------------

  module problem where

  ------------------------------------------------------------------------------

  open import ATP.Metis 2 public
  open import Data.PropFormula 2 public

  ------------------------------------------------------------------------------

  -- Variables.

  p : PropFormula
  p = Var (# 0)

  q : PropFormula
  q = Var (# 1)

  -- Axiom.

  a₁ : PropFormula
  a₁ = ((p ⊃ q) ∧ (q ⊃ p))

  -- Premise.

  Γ : Ctxt
  Γ = [ a₁ ]

  -- Conjecture.

  goal : PropFormula
  goal = ((p ∨ q) ⊃ (p ∧ q))

  -- Subgoals.

  subgoal₀ : PropFormula
  subgoal₀ = ((p ∨ q) ⊃ p)

  subgoal₁ : PropFormula
  subgoal₁ = (((p ∨ q) ∧ p) ⊃ q)

  ------------------------------------------------------------------------------
  -- Proof of subgoal₀.
  ------------------------------------------------------------------------------

  proof₀ : Γ ⊢ subgoal₀
  proof₀ =
    (RAA
      (resolve-thm ⊥ p
        (resolve-thm p q
          (simplify-thm q
            (conjunct-thm (p ∨ q)
              (canonicalize-thm ((¬ p) ∧ (p ∨ q))
                (assume {Γ = Γ} (¬ subgoal₀))))
            (conjunct-thm (¬ p)
              (canonicalize-thm ((¬ p) ∧ (p ∨ q))
                (assume {Γ = Γ} (¬ subgoal₀)))))
          (conjunct-thm ((¬ q) ∨ p)
            (canonicalize-thm (((¬ p) ∨ q) ∧ ((¬ q) ∨ p))
              (weaken (¬ subgoal₀)
                (assume {Γ = ∅} a₁)))))
        (conjunct-thm (¬ p)
          (canonicalize-thm ((¬ p) ∧ (p ∨ q))
            (assume {Γ = Γ} (¬ subgoal₀))))))

  ------------------------------------------------------------------------------
  -- Proof of subgoal₁.
  ------------------------------------------------------------------------------

  proof₁ : Γ ⊢ subgoal₁
  proof₁ =
    (RAA
      (simplify-thm ⊥
        (canonicalize-thm ((¬ q) ∧ (p ∧ (p ∨ q)))
          (assume {Γ = Γ} (¬ subgoal₁)))
        (conjunct-thm ((¬ p) ∨ q)
          (canonicalize-thm (((¬ p) ∨ q) ∧ ((¬ q) ∨ p))
            (weaken (¬ subgoal₁)
              (assume {Γ = ∅} a₁))))))

  ------------------------------------------------------------------------------
  -- Proof of the goal.
  ------------------------------------------------------------------------------

  proof : Γ ⊢ goal
  proof =
    ⊃-elim
      strip-thm
      (∧-intro proof₀ proof₁)

Type-checking the proof

Now, we are ready to verify the Metis derivation by type-checking with Agda the reconstructed proof showed above. Make sure the Agda version is 2.6.0.1.

  $ agda --version
  Agda version 2.6.0.1
  $ agda problem.agda

As we can see in the Agda code showed above, the term proof, the proof-term of the Metis derivation is referring to the proof-terms proof₀ and proof₁. Recall, Metis stripes the goal into subgoals to prove it. Therefore, these terms are the proof-terms for the refutations of the subgoals s₀ and s₁. We show in the following sections the respective natural deduction trees for these refutations.

Refutation tree for the subgoal s₀

For this subgoal, its respective TSTP derivation is the following:

  fof(premise, axiom, (p ⊃ q) ∧ (q ⊃ p)).
  fof(goal, conjecture, (p ∨ q) ⊃ (p ∧ q)).
  fof(s₀, (p ∨ q) ⊃ p, inf(strip, goal)).
  ...
  fof(neg₀, ¬ ((p ∨ q) ⊃ p), inf(negate, s₀)).
  fof(n₀₀, (¬ p ∨ q) ∧ (¬ q ∨ p), inf(canonicalize, premise)).
  fof(n₀₁, ¬ q ∨ p, inf(conjunct, n₀₀)).
  fof(n₀₂, ¬ p ∧ (p ∨ q), inf(canonicalize, neg₀)).
  fof(n₀₃, p ∨ q, inf(conjunct, n₀₂)).
  fof(n₀₄, ¬ p, inf(conjunct, n₀₂)).
  fof(n₀₅, q, inf(simplify, [n₀₃, n₀₄])).
  cnf(r₀₀, ¬ q ∨ p, inf(canonicalize, n₀₁)).
  cnf(r₀₁, q, inf(canonicalize, n₀₅)).
  cnf(r₀₂, p, inf(resolve, q, [r₀₁, r₀₀])).
  cnf(r₀₃, ¬ p, inf(canonicalize, n₀₄)).
  cnf(r₀₄, ⊥, inf(resolve, p, [r₀₂, r₀₃])).
  ...

The refutation tree is the following:

\begin{prooftree} \AxiomC{$\mathcal{D}_1$} %\AxiomC{$\mathcal{D}_3$} \AxiomC{} \RightLabel{assume $\neg s_{0}$} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg s_{0}$} % \UnaryInfC{$\Gamma, \neg s_{0} \vdash (p \vee q) \supset p$} %\LeftLabel{$(\mathcal{D}_3)$\hspace{1.5cm}} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p \wedge (p \vee q)$} \RightLabel{conjunct} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p$} \RightLabel{resolve with $ℓ = p$} \LeftLabel{$(\mathcal{R}_{1})$\hspace{2mm}} \BinaryInfC{$\Gamma, \neg s_{0} \vdash \bot$} \RightLabel{RAA.} \UnaryInfC{$\Gamma \vdash s_{0}$} \end{prooftree}

\begin{prooftree} \AxiomC{$\mathcal{D}_2$} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg q \vee p$} \AxiomC{$\mathcal{D}_3$} \UnaryInfC{$\Gamma, \neg s_{0} \vdash p \vee q$} % \AxiomC{$\mathcal{D}_4$} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p$} % %\LeftLabel{$(\mathcal{D}_4)$\hspace{1.5cm}} \RightLabel{simplify} \BinaryInfC{$\Gamma, \neg s_{0} \vdash q$} \LeftLabel{$(\mathcal{D}_1)$\hspace{2mm}} \RightLabel{resolve~with $ℓ = q$} \BinaryInfC{$\Gamma, \neg s_{0} \vdash p$} \end{prooftree}

\begin{prooftree} \AxiomC{} \RightLabel{axiom premise} \UnaryInfC{$\Gamma \vdash (p \supset q) \wedge (q \supset p)$} \RightLabel{weaken} \UnaryInfC{$\Gamma, \neg s_{0} \vdash (p \supset q) \wedge (q \supset p)$} \LeftLabel{$(\mathcal{D}_2)$\hspace{2mm}} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{0} \vdash (\neg p \vee q) \wedge (\neg q \vee p)$} \RightLabel{conjunct} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg q \vee p$} \end{prooftree}

\begin{prooftree} \AxiomC{} \RightLabel{assume} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg s_{0}$} \LeftLabel{$(\mathcal{D}_3)$\hspace{2mm}} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p \wedge (p \vee q)$} \RightLabel{conjunct} \UnaryInfC{$\Gamma, \neg s_{0} \vdash p \vee q$} \end{prooftree}

\begin{prooftree} \AxiomC{} \RightLabel{assume $\neg s_{0}$} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg s_{0}$} % \UnaryInfC{$\Gamma, \neg s_{0} \vdash (p \vee q) \supset p$} \LeftLabel{$(\mathcal{D}_4)$\hspace{2mm}} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p \wedge (p \vee q)$} \RightLabel{conjunct} \UnaryInfC{$\Gamma, \neg s_{0} \vdash \neg p$} \end{prooftree}

Refutation tree for the subgoal s₁

For this subgoal, its respective TSTP derivation is the following:

  fof(premise, axiom, (p ⊃ q) ∧ (q ⊃ p)).
  ...
  fof(s₁, ((p ∨ q) ∧ p) ⊃ q, inf(strip, goal)).
  ...
  fof(neg₁, ¬ (((p ∨ q) ∧ p) ⊃ q), inf(negate, s₁)).
  fof(n₁₀, ¬ q ∧ p ∧ (p ∨ q), inf(canonicalize, neg₁)).
  fof(n₁₁, (¬ p ∨ q) ∧ (¬ q ∨ p), inf(canonicalize, premise)).
  fof(n₁₂, ¬ p ∨ q, inf(conjunct, n₁₁)).
  fof(n₁₃, ⊥, inf(simplify, [n₁₀, n₁₂])).
  cnf(r₁₀, ⊥, inf(canonicalize, n₁₃)).

The refutation tree is the following:

\begin{prooftree} \AxiomC{} \RightLabel{assume ($\neg s_{1})$} \UnaryInfC{$\Gamma,\neg s_{1} \vdash \neg s_{1}$} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{1}⊢ \neg q \wedge p \wedge (p \vee q)$} \AxiomC{} \RightLabel{axiom premise} \UnaryInfC{$\Gamma \vdash (p \supset q) \wedge (q \supset p)$} \RightLabel{weaken} \UnaryInfC{$\Gamma, \neg s_{1} \vdash (p \supset q) \wedge (q \supset p)$} \RightLabel{canonicalize} \UnaryInfC{$\Gamma, \neg s_{1} \vdash (\neg p \vee q) \wedge (\neg q \vee p)$} \RightLabel{conjunct} \UnaryInfC{$\Gamma, \neg s_{1} \vdash \neg p \vee q$} \LeftLabel{$(\mathcal{R}_{2})$\hspace{1mm}} \RightLabel{simplify} \BinaryInfC{$\Gamma, \neg s_{1} \vdash \bot$} \RightLabel{RAA.} \UnaryInfC{$\Gamma \vdash s_{1}$} \end{prooftree}

The proof of the goal

\begin{prooftree} \AxiomC{} \RightLabel{strip} \UnaryInfC{$\Gamma \vdash (s_{0} \wedge s_{1}) \supset \text{goal}$} \AxiomC{$\mathcal{R}_{1}$} \UnaryInfC{$\Gamma \vdash s_{0}$} \AxiomC{$\mathcal{R}_2$} \UnaryInfC{$\Gamma \vdash s_{1}$} \RightLabel{$\wedge$-intro} \BinaryInfC{$\Gamma \vdash s_{0} \wedge s_{1}$} \RightLabel{$\supset$-elim} \BinaryInfC{$\Gamma \vdash \text{goal}$} \end{prooftree}

Remark : Metis does not print out the above proof where the explicit use of subgoals is necessary to prove the goal. In our Agda file we did.

Issue Tracking

Please report any inconsistency to improve this work by opening an issue. Thanks!

About

Translates Metis ATP proofs to the Agda code

Topics

haskell theorem-proving proof-assistant type-theory agda

Resources

Readme

License

MIT license
Activity

Stars

6 stars

Watchers

1 watching

Forks

2 forks
Report repository

Releases 2

Minor fixes Latest
Dec 22, 2017
+ 1 release

Packages

No packages published

Contributors 2

  •  
  •  

Languages