N-Bit-Adder

This Scheme program calculates the sum of arbitrarily large binary numbers by simulating an N-bit Adder Circuit by recursively using a Full Adder function constructed by AND, OR, XOR logic gates

Logic Design

Full Adder

A 1-Bit Adder circuit takes in three inputs of 1 bit each, where "a" and "b" are operands to be added and "Cin" is the carry-in value. The inputs go through a series of logic gates to generate two output values of "S" which is the sum bit and "Cout" which is the carry-out value. The program displays a complete truth table of each logic gate and a Full Adder.

N-Bit Adder

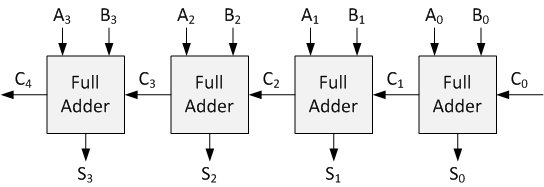
An N-bit Adder is sequence of N connected Full Adders where the carry-out value generated by the previous circuit is the carry-in for the next. This is useful for the addition of binary numbers with an arbitrarily large number of bits.

Usage

A user may provide two arbitrary large binary numbers each of length N to be added using the N-Bit Adder and expect an output of the final carry-out value followed by the rest of the sum.
The binary numbers must be defined within the program as lists in Scheme.
After defining these lists, the n-bit-adder function must be called in this format: n-bit-adder(list1, list2, n)
with the predefined lists as parameters and n being the length of the numbers.
There are comments at the end of the file denoting where a user may create test cases. If the numbers provided are of different lengths this error message will print in place of the output: "Error: The numbers entered must have the same number of bits".
Here there are default test cases of varying lengths to demonstrate the N-Bit Adder on 4, 8, 16, and 32 bit binary numbers.

To run this program, install DrRacket and choose "R5RS" from the language menu

Test Cases

Default Output:

AND-GATE TRUTH TABLE: 
0 0 0
0 1 0
1 0 0
1 1 1

OR-GATE TRUTH TABLE: 
0 0 0
0 1 1
1 0 1
1 1 1

XOR-GATE TRUTH TABLE: 
0 0 0
0 1 1
1 0 1
1 1 0

FULL ADDER TRUTH TABLE: 
INPUTS    OUTPUTS
A B C-in  Sum C-out
0 0 0     (0 . 0)
0 0 1     (1 . 0)
0 1 0     (1 . 0)
0 1 1     (0 . 1)
1 0 0     (1 . 0)
1 0 1     (0 . 1)
1 1 0     (0 . 1)
1 1 1     (1 . 1)

Input 1:

(define A1 '(0 1 0 1) ) ;5 (decimal value) 
(define A2 '(1 0 1 1) ) ;11 

Expected Output 1:

ADDITION OF BINARY NUMBERS 
(0 1 0 1) 
(1 0 1 1) 
WITH A 4-BIT ADDER: 
((1) 0 0 0 0) 

Input 2:

(define B1 '(0 1 0 1 1 0 1 1) ) ;91
(define B2 '(1 0 1 1 0 0 1 0) ) ;178

Expected Output 2:

ADDITION OF BINARY NUMBERS 
(0 1 0 1 1 0 1 1)
(1 0 1 1 0 0 1 0)
WITH A 8-BIT ADDER: 
((1) 0 0 0 0 1 1 0 1)

Input 3:

(define C1 '(1 1 0 1 1 0 1 1 1 0 1 1 0 0 1 0) ) ;56242
(define C2 '(1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 0) ) ;60734	

Expected Output 3:

ADDITION OF BINARY NUMBERS 
(1 1 0 1 1 0 1 1 1 0 1 1 0 0 1 0)
(1 1 1 0 1 1 0 1 0 0 1 1 1 1 1 0)
WITH A 16-BIT ADDER: 
((1) 1 1 0 0 1 0 0 0 1 1 1 1 0 0 0 0)

Input 4:

(define D1 '(1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1) )	;4294967295
(define D2 '(1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0) ) ;2863311530

Expected Output 4:

ADDITION OF BINARY NUMBERS 
(1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1)
(1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0)
WITH A 32-BIT ADDER: 
((1) 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1)