|
| 1 | +--- |
| 2 | +title: "Classification: premier modèle avec les SVM" |
| 3 | +weight: 30 |
| 4 | +slug: SVM |
| 5 | +tags: |
| 6 | + - scikit |
| 7 | + - Machine Learning |
| 8 | + - US elections |
| 9 | + - classification |
| 10 | + - SVM |
| 11 | + - Modélisation |
| 12 | + - Exercice |
| 13 | +categories: |
| 14 | + - Modélisation |
| 15 | + - Exercice |
| 16 | +description: | |
| 17 | + La classification permet d'attribuer une classe d'appartenance (_label_ |
| 18 | + dans la terminologie du _machine learning_) |
| 19 | + discrète à des données à partir de certaines variables explicatives |
| 20 | + (_features_ dans la même terminologie). |
| 21 | + Les algorithmes de classification sont nombreux. L'un des plus intuitifs et |
| 22 | + les plus fréquemment rencontrés sont les _SVM_ (*Support Vector Machine*). |
| 23 | + Ce chapitre illustre les enjeux de la classification à partir de |
| 24 | + ce modèle sur les données de vote aux élections présidentielles US de 2020. |
| 25 | +image: featured_svm.png |
| 26 | +echo: false |
| 27 | +--- |
| 28 | + |
| 29 | + |
| 30 | +{{< badges |
| 31 | + printMessage="true" |
| 32 | +>}} |
| 33 | +
|
| 34 | +# Introduction |
| 35 | + |
| 36 | +Ce chapitre vise à présenter de manière très succincte le principe de l'entraînement de modèles dans un cadre de classification. L'objectif est d'illustrer la démarche à partir d'un algorithme dont le principe est assez intuitif. Il s'agit d'illustrer quelques uns des concepts évoqués dans les chapitres précédents, notamment ceux relatifs à l'entraînement d'un modèle. D'autres cours de votre scolarité vous permettront de découvrir d'autres algorithmes de classification et les limites de chaque technique. |
| 37 | + |
| 38 | + |
| 39 | +## Données |
| 40 | + |
| 41 | + |
| 42 | +{{< include _import_data_ml.qmd >}} |
| 43 | + |
| 44 | +## La méthode des _SVM_ (_Support Vector Machines_) |
| 45 | + |
| 46 | +Les SVM (_Support Vector Machines_) font partie de la boîte à outil traditionnelle des _data scientists_. |
| 47 | +Le principe de cette technique est relativement intuitif grâce à son interprétation géométrique. |
| 48 | +Il s'agit de trouver une droite, avec des marges (les supports) qui discrimine au mieux le nuage de point de nos données. |
| 49 | +Bien-sûr, dans la vraie vie, il est rare d'avoir des nuages de points bien ordonnés pour pouvoir les séparer par une droite. Mais une projection adéquate (un noyau ou _kernel_) peut arranger des données pour permettre de discriminer les données. |
| 50 | + |
| 51 | +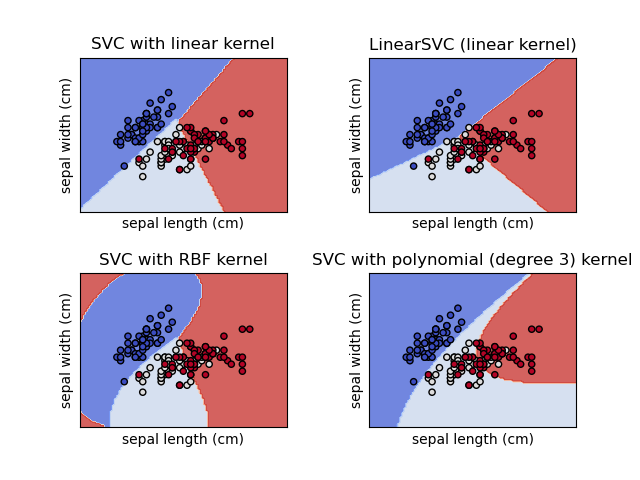 |
| 52 | + |
| 53 | + |
| 54 | +::: {.tip collapse="true"} |
| 55 | +## Formalisation mathématique |
| 56 | + |
| 57 | +Les SVM sont l'une des méthodes de _machine learning_ les plus intuitives |
| 58 | +du fait de l'interprétation géométrique simple de la méthode. Il s'agit |
| 59 | +aussi d'un des algorithmes de _machine learning_ à la formalisation |
| 60 | +la moins complexe pour les praticiens ayant des notions en statistique |
| 61 | +traditionnelle. Cette note revient dessus. Néanmoins, |
| 62 | +celle-ci n'est pas nécessaire à la compréhension du chapitre. |
| 63 | +En _machine learning_, plus que les détails mathématiques, l'important |
| 64 | +est d'avoir des intuitions. |
| 65 | + |
| 66 | +L'objectif des SVM est, rappelons-le, de trouver un hyperplan qui permette |
| 67 | +de séparer les différentes classes au mieux. Par exemple, dans un espace |
| 68 | +à deux dimensions, il s'agit de trouver une droite avec des marges |
| 69 | +qui permette de séparer au mieux l'espace en partie avec |
| 70 | +des _labels_ homogènes. |
| 71 | + |
| 72 | +On peut, sans perdre de généralité, |
| 73 | +supposer que le problème consiste à supposer l'existence d'une loi de probabilité $\mathbb{P}(x,y)$ ($\mathbb{P} \to \{-1,1\}$) qui est inconnue. Le problème de discrimination |
| 74 | +vise à construire un estimateur de la fonction de décision idéale qui minimise la probabilité d'erreur. Autrement dit |
| 75 | + |
| 76 | +$$ |
| 77 | +\theta = \arg\min_\Theta \mathbb{P}(h_\theta(X) \neq y |x) |
| 78 | +$$ |
| 79 | + |
| 80 | +Les SVM les plus simples sont les SVM linéaires. Dans ce cas, on suppose qu'il existe un séparateur linéaire qui permet d'associer chaque classe à son signe: |
| 81 | + |
| 82 | +$$ |
| 83 | +h_\theta(x) = \text{signe}(f_\theta(x)) ; \text{ avec } f_\theta(x) = \theta^T x + b |
| 84 | +$$ |
| 85 | +avec $\theta \in \mathbb{R}^p$ et $w \in \mathbb{R}$. |
| 86 | + |
| 87 | +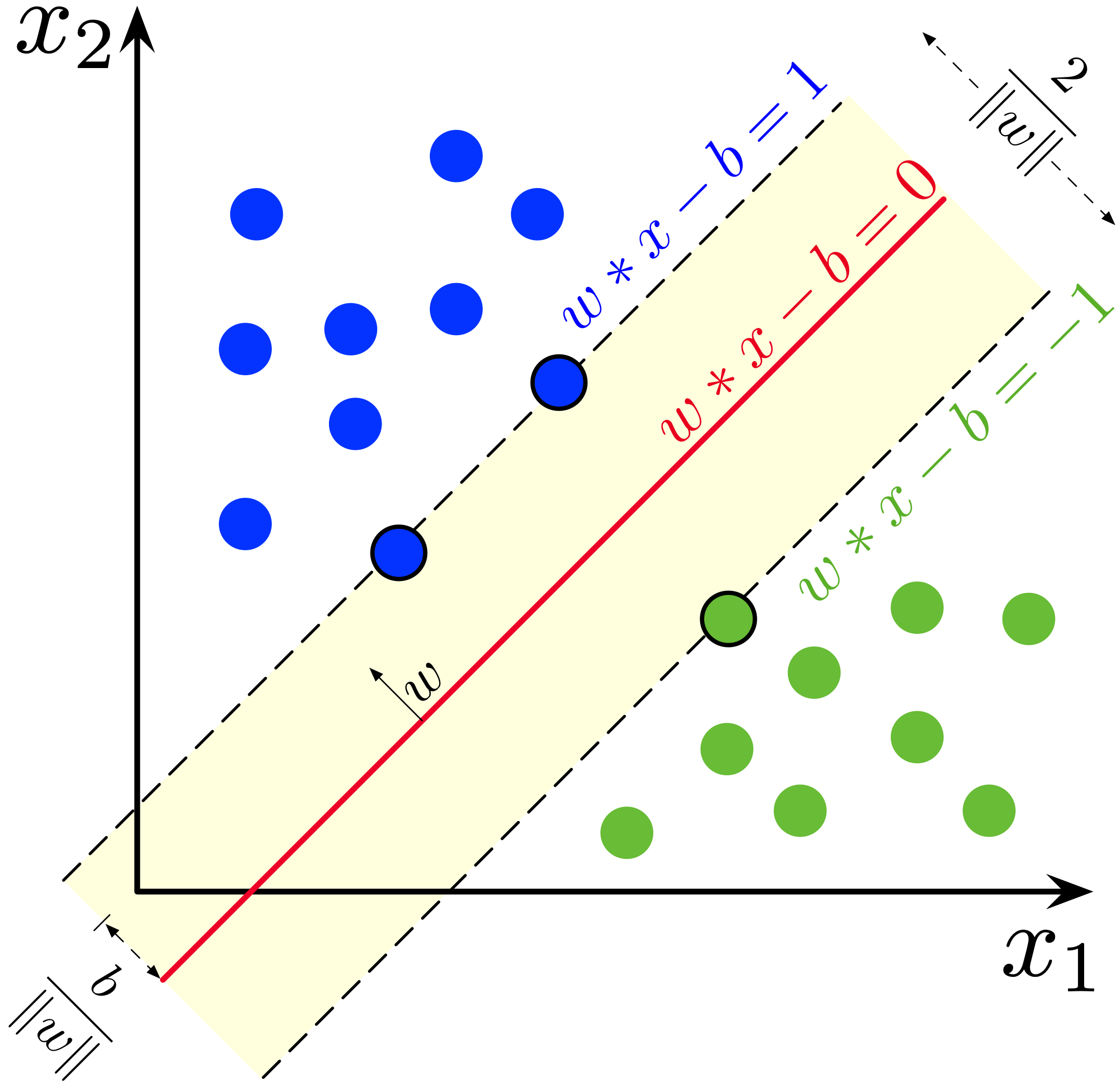{width="60%"} |
| 88 | + |
| 89 | +Lorsque des observations sont linéairement séparables, |
| 90 | +il existe une infinité de frontières de décision linéaire séparant les deux classes. Le _"meilleur"_ choix est de prendre la marge maximale permettant de séparer les données. La distance entre les deux marges est $\frac{2}{||\theta||}$. Donc maximiser cette distance entre deux hyperplans revient à minimiser $||\theta||^2$ sous la contrainte $y_i(\theta^Tx_i + b) \geq 1$. |
| 91 | + |
| 92 | +Dans le cas non linéairement séparable, la *hinge loss* $\max\big(0,y_i(\theta^Tx_i + b)\big)$ permet de linéariser la fonction de perte, ce qui donne le programme d'optimisation suivant : |
| 93 | + |
| 94 | +$$ |
| 95 | +\frac{1}{n} \sum_{i=1}^n \max\big(0,y_i(\theta^Tx_i + b)\big) + \lambda ||\theta||^2 |
| 96 | +$$ |
| 97 | + |
| 98 | +La généralisation au cas non linéaire implique d'introduire des noyaux transformant l'espace de coordonnées des observations. |
| 99 | + |
| 100 | +::: |
| 101 | + |
| 102 | + |
| 103 | +## Application |
| 104 | + |
| 105 | +Pour appliquer un modèle de classification, il nous faut |
| 106 | +trouver une variable dichotomique. Le choix naturel est |
| 107 | +de prendre la variable dichotomique qu'est la victoire ou |
| 108 | +défaite d'un des partis. |
| 109 | + |
| 110 | +Même si les Républicains ont perdu en 2020, ils l'ont emporté |
| 111 | +dans plus de comtés (moins peuplés). Nous allons considérer |
| 112 | +que la victoire des Républicains est notre _label_ 1 et la défaite _0_. |
| 113 | + |
| 114 | +```{python} |
| 115 | +#| echo: true |
| 116 | +# packages utiles |
| 117 | +from sklearn import svm |
| 118 | +import sklearn.metrics |
| 119 | +from sklearn.model_selection import train_test_split |
| 120 | +from sklearn.model_selection import cross_val_score |
| 121 | +import matplotlib.pyplot as plt |
| 122 | +``` |
| 123 | + |
| 124 | +::: {.exercise} |
| 125 | +## Exercice 1 : Premier algorithme de classification |
| 126 | + |
| 127 | +1. Créer une variable *dummy* appelée `y` dont la valeur vaut 1 quand les républicains l'emportent. |
| 128 | +2. En utilisant la fonction prête à l'emploi nommée `train_test_split` de la librairie `sklearn.model_selection`, |
| 129 | +créer des échantillons de test (20 % des observations) et d'estimation (80 %) avec comme *features* : `'Unemployment_rate_2019', 'Median_Household_Income_2019', 'Percent of adults with less than a high school diploma, 2015-19', "Percent of adults with a bachelor's degree or higher, 2015-19"` et comme *label* la variable `y`. |
| 130 | + |
| 131 | +*Note: Il se peut que vous ayez le warning suivant :* |
| 132 | + |
| 133 | +> A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel() |
| 134 | +
|
| 135 | +*Note : Pour éviter ce warning à chaque fois que vous estimez votre modèle, vous pouvez utiliser `DataFrame[['y']].values.ravel()` plutôt que `DataFrame[['y']]` lorsque vous constituez vos échantillons.* |
| 136 | + |
| 137 | +3. Entraîner un classifieur SVM avec comme paramètre de régularisation `C = 1`. Regarder les mesures de performance suivante : `accuracy`, `f1`, `recall` et `precision`. |
| 138 | + |
| 139 | +4. Vérifier la matrice de confusion : vous devriez voir que malgré des scores en apparence pas si mauvais, il y a un problème notable. |
| 140 | + |
| 141 | +5. Refaire les questions précédentes avec des variables normalisées. Le résultat est-il différent ? |
| 142 | + |
| 143 | +6. Changer de variables *x*. Utiliser uniquement le résultat passé du vote démocrate (année 2016) et le revenu. Les variables en question sont `share_2016_republican` et `Median_Household_Income_2019`. Regarder les résultats, notamment la matrice de confusion. |
| 144 | + |
| 145 | +7. [OPTIONNEL] Faire une 5-fold validation croisée pour déterminer le paramètre *C* idéal. |
| 146 | + |
| 147 | +::: |
| 148 | + |
| 149 | + |
| 150 | +```{python} |
| 151 | +# 1. Création de la dummy y de victoire des républicains |
| 152 | +votes['y'] = (votes['votes_gop'] > votes['votes_dem']).astype(int) |
| 153 | +``` |
| 154 | + |
| 155 | + |
| 156 | +```{python} |
| 157 | +#2. Création des échantillons d'entraînement et de validation |
| 158 | +xvars = ['Unemployment_rate_2019', 'Median_Household_Income_2019', 'Percent of adults with less than a high school diploma, 2015-19', "Percent of adults with a bachelor's degree or higher, 2015-19"] |
| 159 | +
|
| 160 | +df = votes.loc[:, ["y"] + xvars] |
| 161 | +
|
| 162 | +X_train, X_test, y_train, y_test = train_test_split( |
| 163 | + df[xvars], |
| 164 | + df[['y']].values.ravel(), test_size=0.2, random_state=123 |
| 165 | +) |
| 166 | +#X_train.head() |
| 167 | +#y_test |
| 168 | + |
| 169 | +``` |
| 170 | + |
| 171 | + |
| 172 | + |
| 173 | + |
| 174 | +```{python} |
| 175 | +# 3. Entraînement du modèle et performances |
| 176 | +clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train) |
| 177 | +y_pred = clf.predict(X_test) |
| 178 | +
|
| 179 | +sc_accuracy = sklearn.metrics.accuracy_score(y_pred, y_test) |
| 180 | +sc_f1 = sklearn.metrics.f1_score(y_pred, y_test) |
| 181 | +sc_recall = sklearn.metrics.recall_score(y_pred, y_test) |
| 182 | +sc_precision = sklearn.metrics.precision_score(y_pred, y_test) |
| 183 | +
|
| 184 | +#print(sc_accuracy) |
| 185 | +#print(sc_f1) |
| 186 | +#print(sc_recall) |
| 187 | +#print(sc_precision) |
| 188 | +``` |
| 189 | + |
| 190 | +A l'issue de la question 3, |
| 191 | +le classifieur avec `C = 1` |
| 192 | +devrait avoir les performances suivantes : |
| 193 | + |
| 194 | +```{python} |
| 195 | +#| output: asis |
| 196 | +out = pd.DataFrame.from_dict({"Accuracy": [sc_accuracy], "Recall": [sc_recall], |
| 197 | + "Precision": [sc_precision], "F1": [sc_f1]}, orient = "index", columns = ["Score"]) |
| 198 | +print(out.to_markdown()) |
| 199 | +``` |
| 200 | + |
| 201 | + |
| 202 | +```{python} |
| 203 | +#| output: false |
| 204 | +
|
| 205 | +# 4. Matrice de confusion |
| 206 | +predictions = clf.predict(X_test) |
| 207 | +cm = sklearn.metrics.confusion_matrix(y_test, predictions, labels=clf.classes_) |
| 208 | +disp = sklearn.metrics.ConfusionMatrixDisplay( |
| 209 | + confusion_matrix=cm, |
| 210 | + display_labels=clf.classes_ |
| 211 | + ) |
| 212 | +disp.plot() |
| 213 | +
|
| 214 | +#Réponse : Notre classifieur manque totalement les labels 0, qui sont minoritaires. |
| 215 | +#Une raison possible ? L'échelle des variables : le revenu a une |
| 216 | +#distribution qui peut écraser celle des autres variables, |
| 217 | +#dans un modèle linéaire. Il faut donc, a minima, |
| 218 | +#standardiser les variables. |
| 219 | +
|
| 220 | +plt.savefig("confusion_matrix.png") |
| 221 | +``` |
| 222 | + |
| 223 | +La matrice de confusion associée |
| 224 | +prend cette forme: |
| 225 | + |
| 226 | + |
| 227 | + |
| 228 | + |
| 229 | +```{python} |
| 230 | +#| output: false |
| 231 | +
|
| 232 | +# 5. Refaire les questions précédentes avec des variables normalisées. |
| 233 | +import sklearn.preprocessing as preprocessing |
| 234 | +
|
| 235 | +X = df[xvars] |
| 236 | +y = df[['y']] |
| 237 | +scaler = preprocessing.StandardScaler().fit(X) #Ici on standardise |
| 238 | +X = scaler.transform(X) #Ici on standardise |
| 239 | +
|
| 240 | +X_train, X_test, y_train, y_test = train_test_split( |
| 241 | + X, |
| 242 | + y.values.ravel(), test_size=0.2, random_state=0 |
| 243 | +) |
| 244 | +
|
| 245 | +clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train) |
| 246 | +predictions = clf.predict(X_test) |
| 247 | +cm = sklearn.metrics.confusion_matrix(y_test, predictions, labels=clf.classes_) |
| 248 | +disp = sklearn.metrics.ConfusionMatrixDisplay( |
| 249 | + confusion_matrix=cm, |
| 250 | + display_labels=clf.classes_ |
| 251 | + ) |
| 252 | +disp.plot() |
| 253 | +
|
| 254 | +#Réponse : Non, standardiser les variables n'apporte pas de gain |
| 255 | +# Il faut donc aller plus loin : le problème ne vient pas de l'échelle mais du choix des variables. |
| 256 | +# C'est pour cette raison que l'étape de sélection de variable est cruciale. |
| 257 | +
|
| 258 | +plt.savefig("confusion_matrix2.png") |
| 259 | +``` |
| 260 | + |
| 261 | + |
| 262 | + |
| 263 | + |
| 264 | +A l'issue de la question 6, |
| 265 | +le nouveau classifieur avec devrait avoir les performances suivantes : |
| 266 | + |
| 267 | +```{python} |
| 268 | +#| output: asis |
| 269 | +
|
| 270 | +out = pd.DataFrame.from_dict({"Accuracy": [sc_accuracy], "Recall": [sc_recall], |
| 271 | + "Precision": [sc_precision], "F1": [sc_f1]}, orient = "index", columns = ["Score"]) |
| 272 | +print(out.to_markdown()) |
| 273 | +``` |
| 274 | + |
| 275 | + |
| 276 | + |
| 277 | + |
| 278 | +```{python} |
| 279 | +#| include: false |
| 280 | +
|
| 281 | +# 6. Refaire les questions en changeant la variable X. |
| 282 | +votes['y'] = (votes['votes_gop'] > votes['votes_dem']).astype(int) |
| 283 | +df = votes[["y", "share_2016_republican", 'Median_Household_Income_2019']] |
| 284 | +tempdf = df.dropna(how = "any") |
| 285 | +
|
| 286 | +X = votes[['share_2016_republican', 'Median_Household_Income_2019']] |
| 287 | +y = tempdf[['y']] |
| 288 | +scaler = preprocessing.StandardScaler().fit(X) |
| 289 | +X = scaler.transform(X) |
| 290 | +
|
| 291 | +X_train, X_test, y_train, y_test = train_test_split( |
| 292 | + X, |
| 293 | + y.values.ravel(), test_size=0.2, random_state=0 |
| 294 | +) |
| 295 | +
|
| 296 | +clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train) |
| 297 | +y_pred = clf.predict(X_test) |
| 298 | +
|
| 299 | +sc_accuracy = sklearn.metrics.accuracy_score(y_pred, y_test) |
| 300 | +sc_f1 = sklearn.metrics.f1_score(y_pred, y_test) |
| 301 | +sc_recall = sklearn.metrics.recall_score(y_pred, y_test) |
| 302 | +sc_precision = sklearn.metrics.precision_score(y_pred, y_test) |
| 303 | +
|
| 304 | +#print(sc_accuracy) |
| 305 | +#print(sc_f1) |
| 306 | +#print(sc_recall) |
| 307 | +#print(sc_precision) |
| 308 | +
|
| 309 | +predictions = clf.predict(X_test) |
| 310 | +cm = sklearn.metrics.confusion_matrix(y_test, predictions, labels=clf.classes_) |
| 311 | +disp = sklearn.metrics.ConfusionMatrixDisplay( |
| 312 | + confusion_matrix=cm, |
| 313 | + display_labels=clf.classes_ |
| 314 | + ) |
| 315 | +disp.plot() |
| 316 | +# On obtient un résultat beaucoup plus cohérent. |
| 317 | +
|
| 318 | +plt.savefig("confusion_matrix3.png") |
| 319 | +``` |
| 320 | + |
| 321 | +Et la matrice de confusion associée : |
| 322 | + |
| 323 | + |
| 324 | + |
| 325 | + |
| 326 | + |
| 327 | + |
| 328 | + |
| 329 | + |
| 330 | + |
| 331 | + |
| 332 | + |
| 333 | + |
| 334 | + |
| 335 | + |
| 336 | + |
0 commit comments