Toy Lifting Wavelet Animator

This repository contains a toy program which animates various ways of computing of the Discrete Wavelet Transform (DWT). In particular, it animates the integer lifting based DWT defined by the VC-2 (SMPTE ST 2042-1:2017) video codec.

The animations produced by this toy, amongst other things, demonstrates possible implementations of 'streaming' DWTs which can process their input without access to a complete signal. In particular, they illustrate that a filter does not need a copy of the entire stream -- or even an especially large segment of it -- to compute its outputs.

There's nothing novel about streaming DWT computation -- they're just FIR filters after all -- and It is something which almost any commercial VC-2 (or similar) video codec will do, for example. However, its fun to visualise the evaulation process. Of course, real codecs often have multi-level and multi-dimensional transforms in practice but the principles are the same...

Usage

This toy is known to run under Python 3.8 and has no exeternal dependencies.

By default, a block-based (non-streaming) Le Gall wavelet is animated for a random input signal:

$ python streaming_wavelet_toy.py

Different orders of computation can be animated by adding the --order argument:

• block = compute each stage in its entirety, one after the other.
• chained = perform computations as if all lifting stages have been implemented as a chain of FIR filters.
• lazy = compute values only when required to compute each output value in turn.
• lazy_two_steps = like lazy except computes all transform values, then all output values (i.e. separates encoding an decoding).

Different wavelets can be animated using the --wavelet argument:

• deslauriers_dubuc_9_7
• le_gall_5_3
• deslauriers_dubuc_13_7
• haar_no_shift
• haar_with_shift (same as haar_no_shift; see the VC-2 spec for the rest of this rabbit hole...)
• fidelity
• daubechies_9_7

See --help for additional arguments.

Demos

If you can't be bothered to check-out and run 25 KB of code, here Over 10 MB of GIFs showing sample outputs...

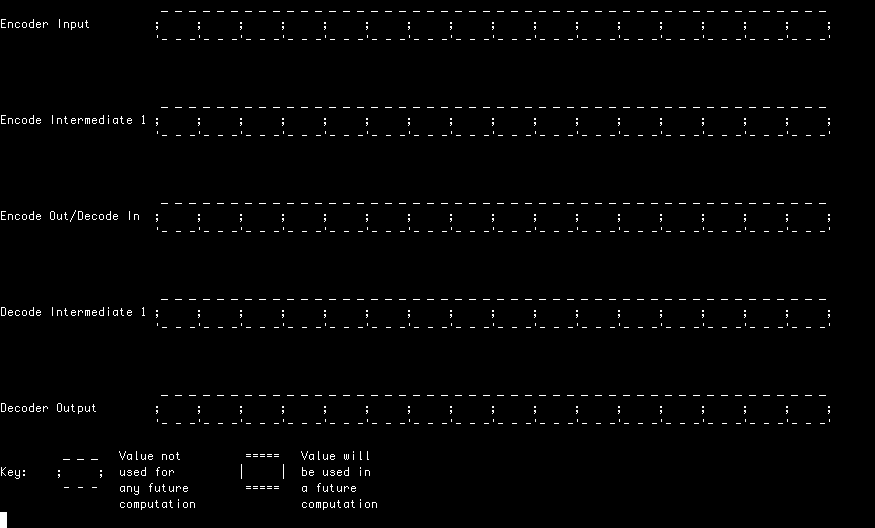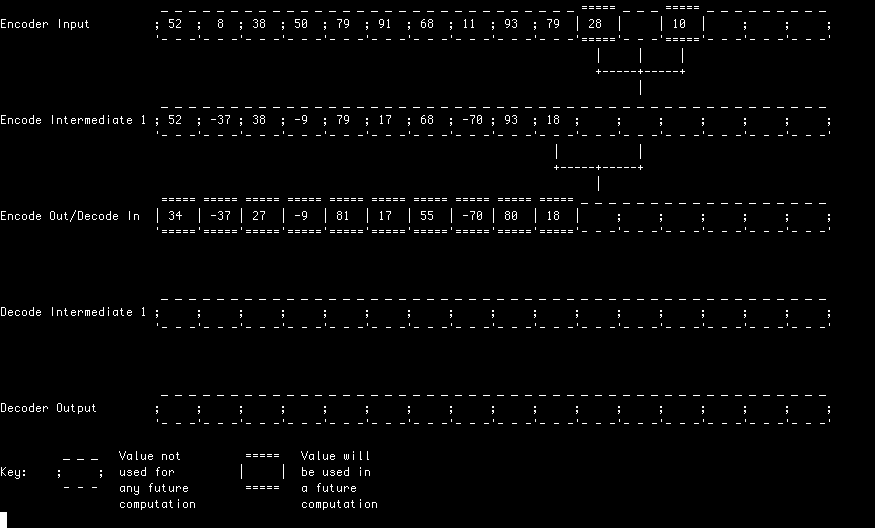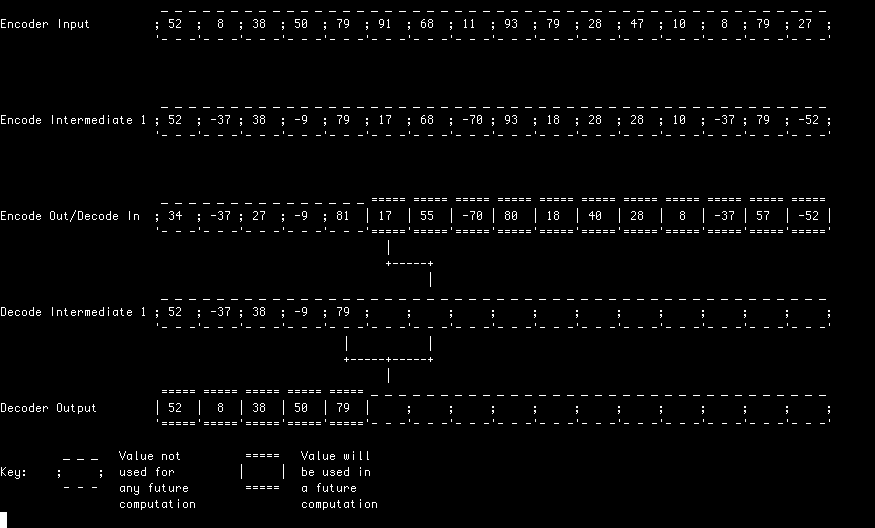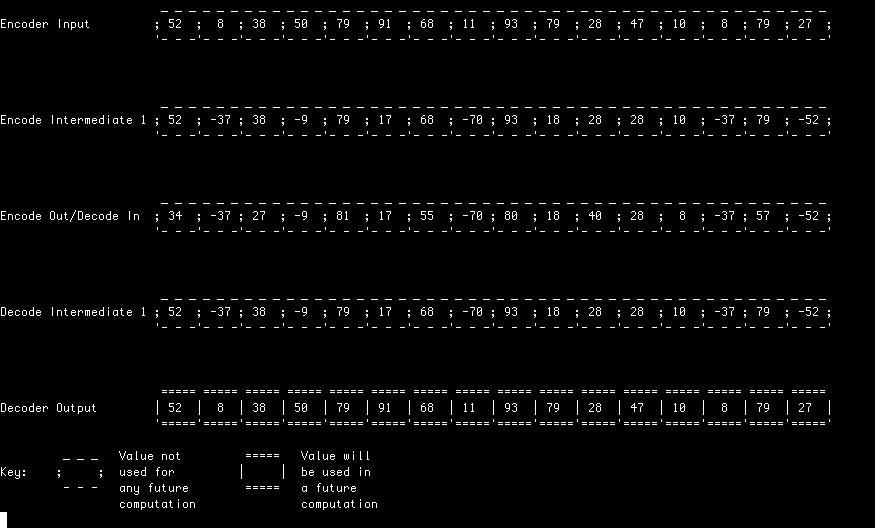
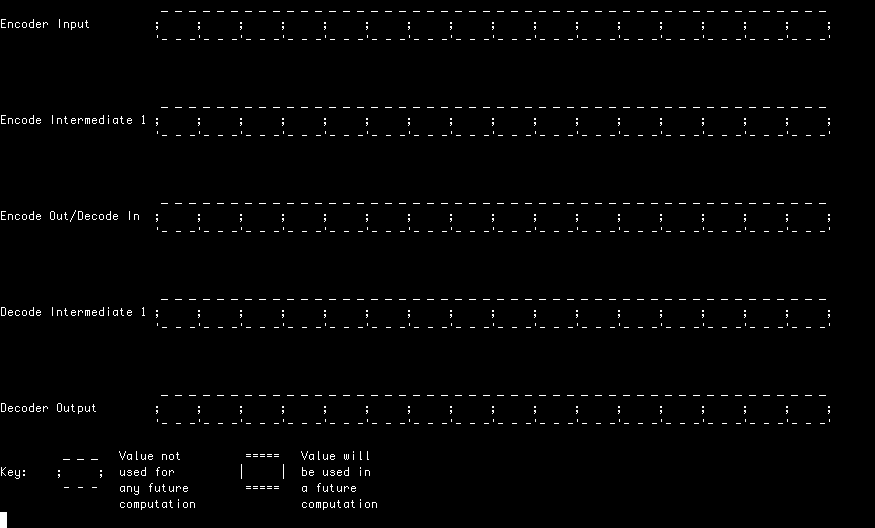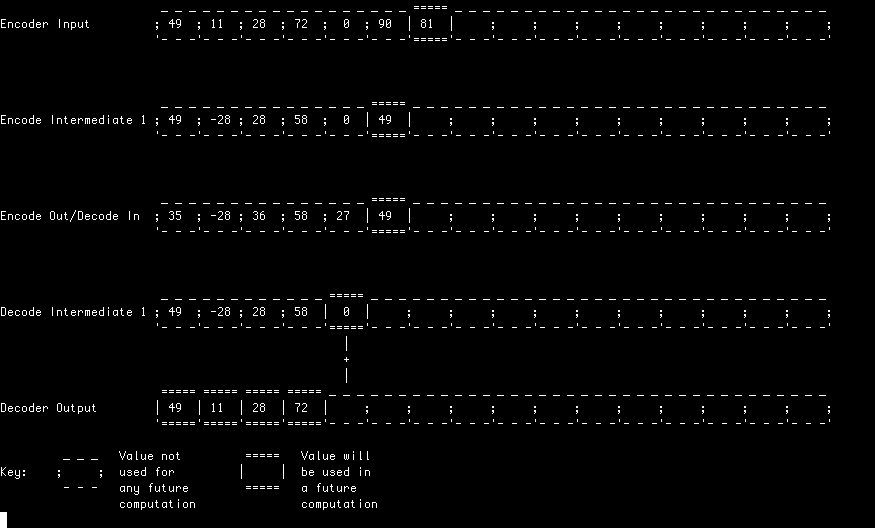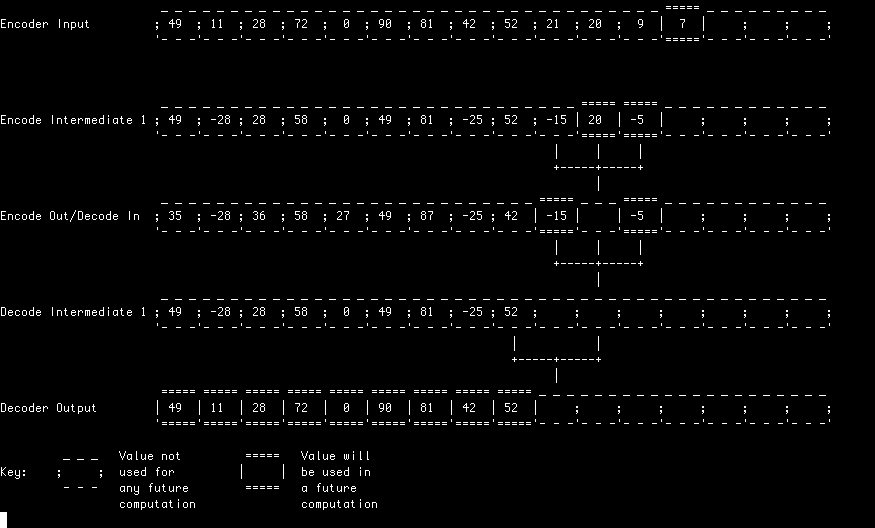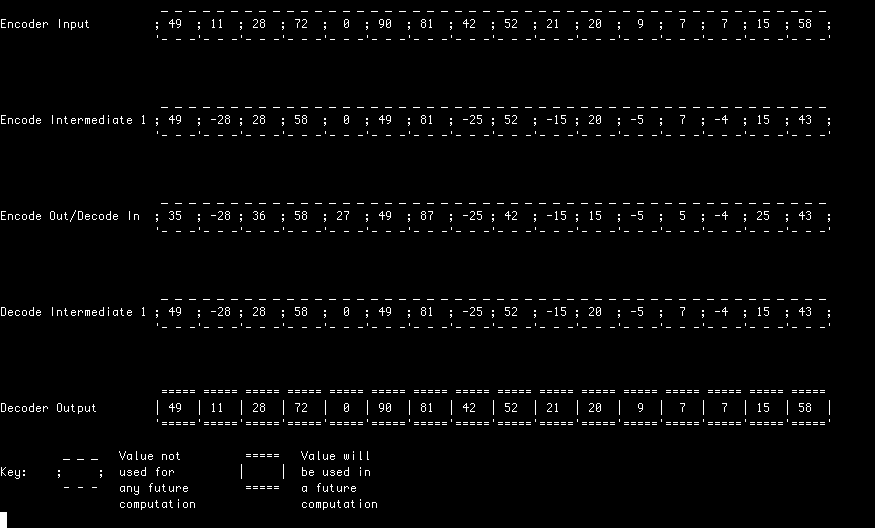
In all of these examples, a random input stream is first encoded (analysed) and decoded (synthesised) using a Le Gall (5, 3) transform.

Block-based evaluation

In this example, each lifting stage is computed in its entirety before starting the next. This simple approach allows an in-place implementation and represents the classic textbook example of how a lifting filter can be implemented.

Chained FIR filters

Here, each lifting stage is performed in a pipeline style arrangement with each filter starting the process the outputs of the previous stage just as they become available.

Lazy evaluation (encode then decode)

In this example, the filter is evaluated lazily meaning values are only computed when they're required to produce a particular output. Note that input values are not necessarily consumed in order(!)

Lazy evaluation (from input)

A bigger filter

This time with the deslauriers_dubuc_9_7 wavelet in which one of the lifting stages is a little more exciting...