MNIST-NNmathsANDnumpy

problem function

MNIST classification problem.

The MNIST dataset is a large database of handwritten digits. The dataset contains 70,000 small images (28 x 28 pixels), each one of them being labeled.

cycle of code & understading

1. forward propagation
2. backward propagation
3. update parameters

Our network will have three layers total: an input layer and two layers with parameters. Because the input layer has no parameters, this network would be referred to as a two-layer neural network.

whole cycle

layers

1. input layer
2. 1 hidden layer of size 10 with ReLu activation function - 1 hidden layer of size 10 with Softmax activation function
3. output

The input layer

has 784 nodes, corresponding to each of the 784 pixels in the 28x28 input image. Each pixel has a value between 0 and 255, with 0 being black and 255 being white. It's common to normalize these values — getting all values between 0 and 1, here by simply dividing by 255 — before giving them in the network.

The second layer, or hidden layer

could have any amount of nodes, but we've made it really simple here with just 10 nodes. The value of each of these nodes is calculated based on weights and biases applied to the value of the 784 nodes in the input layer. After this calculation, a ReLU activation is applied to all nodes in the layer. In a deeper network, there may be multiple hidden layers back to back before the output layer.

The output layer

also has 10 nodes, corresponding to each of the output classes (digits 0 to 9). The value of each of these nodes will again be calculated from weights and biases applied to the value of the 10 nodes in the hidden layer, with a softmax activation applied to them to get the final output.

for each layer, is composed of 2 steps(forward & backward):

1. application of weights and biases
2. computation of the activation function

for forward and backward hidden layer

predictions are made based on the values in the input nodes and the weights. For example you will we have three features in the dataset: X1, X2, and X3, therefore we have three nodes in the first layer, also known as the input layer.

The weights of a neural network are basically the strings that we have to adjust in order to be able to correctly predict our output.

Why do we even need a bias term?

Suppose if we have a person who has input values (0,0,0), the sum of the products of input nodes and weights will be zero. In that case, the output will always be zero no matter how much we train the algorithms. Therefore, in order to be able to make predictions, even if we do not have any non-zero information about the person, we need a bias term. The bias term is necessary to make a robust neural network.

why need of rectified linear unit(ReLU)?

We need to do one more calculation before moving on to the next layer, applying a non-linear activation and making it a linear combination of the input features. That means the hidden layer is essentially useless, and we're just building a linear regression model.To prevent this reduction and actually add complexity with our layers, before passing it off to the next layer. so we will be using it

The Rectified Linear Unit, is an activation function used in artificial neural networks and deep learning models. It's a simple yet effective non-linear activation function that has become very popular in recent years due to its ability to address the vanishing gradient problem and its computational efficiency. advantages

1. Non-Linearity
2. Sparsity
3. Mitigating Vanishing Gradien

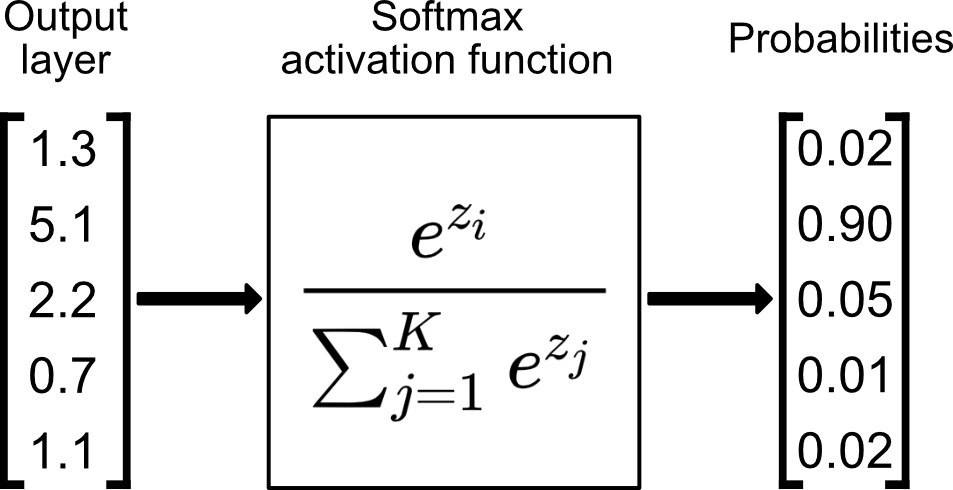
why do use softmax function?

since it is a output layer, use would use softmax function rather than using ReLU

Softmax is a mathematical function that takes a vector of arbitrary real-valued scores and converts them into a probability distribution. It's often used in machine learning and deep learning for multiclass classification problems, where you want to assign an input to one of several possible classes. Given an input vector of scores (also known as logits), the softmax function computes the exponential of each score and then normalizes the results to obtain a set of probabilities that sum up to 1.0.

advantages

1. Softmax squashes the input values into a valid probability distribution.
2. all output values are between 0 and 1.
3. normalises the output values so that they sum up to 1, making them suitable for representing probabilities.

Forward propagation

Z[1]=W[1]X+b[1]

A[1]=gReLU(Z[1]))

Z[2]=W[2]A[1]+b[2]

A[2]=gsoftmax(Z[2])

Backward propagation

dZ[2]=A[2]−Y

dW[2]=1mdZ[2]A[1]T

dB[2]=1mΣdZ[2]

dZ[1]=W[2]TdZ[2].∗g[1]′(z[1])

dW[1]=1mdZ[1]A[0]T

dB[1]=1mΣdZ[1]]

Parameter updates

W[2]:=W[2]−αdW[2]

b[2]:=b[2]−αdb[2]

W[1]:=W[1]−αdW[1]

b[1]:=b[1]−αdb[1]

resources & blogs used:

1. Build an Artificial Neural Network From Scratch
2. Building a Deep Neural Network from Scratch using Numpy
3. Understanding the math behind neural networks by building one from scratch