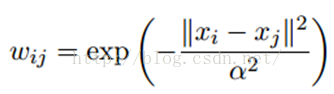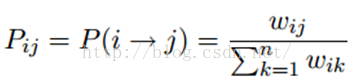半监督学习(LP算法)

1 半监督学习的两个假设

1. 聚类假设。同一个簇的样本拥有同一个标签
2. 流形假设。相近的样本有相似的输出

2 半监督学习分类

1. 纯半监督学
   学习的目的是为了在新的样本上性能更好（为了泛化性能）
2. 直推学习
   学习的目的是为了能更好的预测本样本中无标签的数据（不强调泛化性能）

3 半监督学习和主动学习

主动学习是和外部的专家进行交互，而半监督学习强调的是系统内部的自我学习

4 LabelPropagation算法（标签传播）

1. 构造相似矩阵
2. 传播

4.1 构造相似矩阵

LP算法是基于Graph的，因此需要先构建一个图，图的每一个节点就是一个样本点，边的权值是衡量相连的样本之间的相似性 ，节点i和节点j的边权值计算为：

4.2 传播

假设数据中拥有N个有label的样本，构建NXN的概率转移矩阵:

Pij表示节点从i转移到j的概率。（实际上我们构建的是无相图Pij=Pji）假设样本中有C个类的L个样本，定义一个LxC的矩阵Y1，其中Y1ij表示第i个节点属于第j类的概率，对于有label的数据，因为label是确定的所以，Y1矩阵是一个0/1矩阵； 同样的方法作用到unlabeled的样本中构建一个Y2矩阵，Y2矩阵的值可以随机产生，F=np.vstack([Y1,Y2]),产生F矩阵。
1) 执行传播：F=PF 2) 重置F矩阵中label样本的标签，即：把Y1<-原来的Y1 3) 重复1,2直到F收敛

5 结果

6 总结

LP算法通过构建Graph，计算样本之间的距离，从而获得样本之间的相似矩阵（样本一定要归一化，和计算距离相关的操作，一定要进行归一化）