#Genetic Algorithm Генетический алгоритм, реализация на Python 3.
##Пример использования:
Попробуем найти одно из решений диофантова уравнения (с целочисленными корнями): a + 2b + 3c + 4d = 30.
Фитнес-функция example_diophante получает на вход список предположительных корней уравнения и возвращает
отрицательное расстояние (чем больше фитнес, тем лучше) до его равенства (30).
То есть при корнях являющихся решением, фитнес-функция вернет 0, во всех других случаях отрицательное число,
которое чем ближе к нулю, тем больше наши корни похожи на решение.
def example_diophante(x):
'''Equation: a + 2b + 3c + 4d = 30'''
a, b, c, d = x
z = a + 2*b + 3*c + 4*d
ans = 30
print("a={:3.0f} b={:3.0f} c={:3.0f} d={:3.0f} z={:3.0f}".format(a, b, c, d, z), "- Solved!" if z == ans else "")
return -abs(ans-z)###Параметры конструктора:
- steps = 40 - дадим эволюции не более 40 поколений
- stop_fitness = 0 - останавливаем эволюцию, когда функция вернула 0, значит решение найдено
- bounds = (-100, 100, 1) - предположим корни лежат где-то в диапазоне (-100, 100), шаг единица, поскольку корни целочисленные. От шага зависит точность поиска решения. Иррациональные корни ГА сможет найти с указанной точностью (0-stop_fitness).
- num_genes = 4 - у нас 4 корня
- stagnation = 3 - если эволюция войдет в застой на 3 поколения, применяем катаклизм (более сильная мутация)
- mutagen = "1_step" - у каждой особи (потенциального решения) при рождении создаем мутацию - меняем один из параметров на размер шага
- cata_mutagen = "full_step" - если мы вошли в стагнацию, применяем катаклизм - меняем все параметры на размер шага
- population_limit = 10 - в каждом поколении будем тестировать 10 вариантов решения (особей)
- survive_coef = 0.2 - из каждого поколения выбираем 20% лучших решений (то есть 2 особи из 10 смогут оставить потомков)
- productivity = 4 - на каждую из двух выживших особей после скрещивания приходится 4 потомка, то есть в новом поколении будет 8 потомков, остальные 2 места в популяции займут особи сгенерированные случайным образом
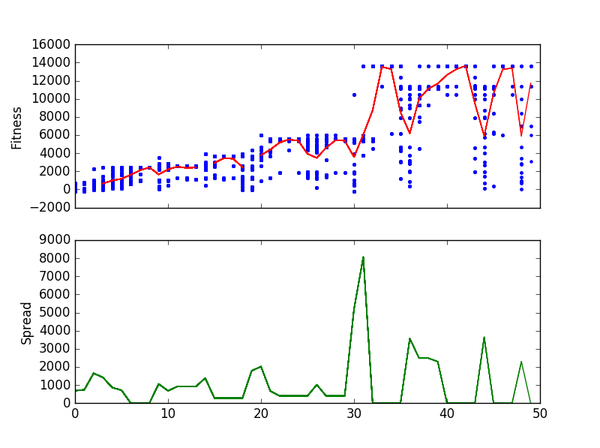
- plot = True - если установлен matplotlib, будем наблюдать эволюционный прогресс на графике
if __name__ == '__main__':
ga = GA(example_equation, bounds=(-100, 100, 1), num_genes=4, steps=40, stop_fitness=0, stagnation=3,
population_limit=10, survive_coef=0.2, productivity=4, mutagen="1_step", cata_mutagen="full_step",
plot=True)
result = ga.evolve()
print("Best solution:", result)Большинство параметров можно оставить по умолчанию, обязательны первые три.
###Результат работы
...
a=-96 b=-73 c= -4 d= 70 z= 26
a=-94 b=-71 c= -3 d= 71 z= 39
a=-94 b=-70 c= -4 d= 71 z= 38
a=-95 b=-71 c= -4 d= 70 z= 31
a=-94 b=-73 c= -4 d= 71 z= 32
a=-95 b=-73 c= -4 d= 69 z= 23
a=-94 b=-71 c= -5 d= 70 z= 29
a=-95 b=-71 c= -4 d= 71 z= 35
a=-18 b= 61 c=-100 d=-87 z=-544
a=-78 b= 74 c= 65 d= 48 z=457
- Step 9 / 40 results: best: -1.000, spread: 0.000, elapsed: 0m 1s, remaining: 0m 0s
a=-94 b=-71 c= -5 d= 69 z= 25
a=-96 b=-71 c= -4 d= 70 z= 30 - Solved!
a=-94 b=-70 c= -4 d= 70 z= 34
a=-94 b=-71 c= -4 d= 69 z= 28
a=-95 b=-71 c= -6 d= 70 z= 25
a=-94 b=-71 c= -6 d= 70 z= 26
a=-94 b=-71 c= -4 d= 69 z= 28
a=-95 b=-72 c= -5 d= 70 z= 26
a= 93 b=-79 c=-95 d=-26 z=-454
a=-42 b=-81 c= 30 d= 13 z=-62
- Step 10 / 40 results: best: 0.000, spread: 2.000, elapsed: 0m 1s, remaining: 0m 0s
- Evolution completed: best fitness = 0.000 <= 0.000
Best solution: ([-96, -71, -4, 70], 0)