PyAbel README

Note: This readme is best viewed as part of the PyAbel Documentation.

Introduction

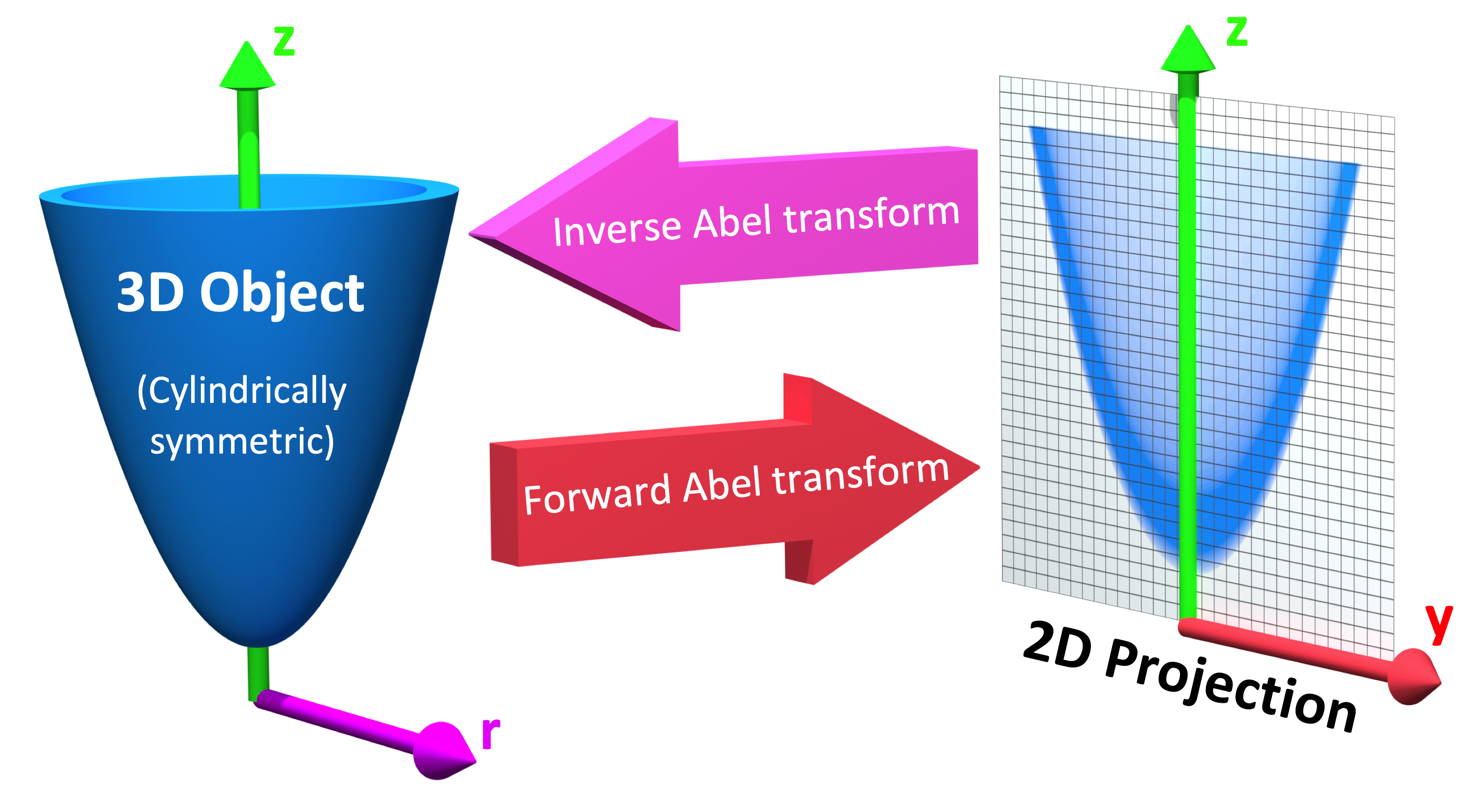
PyAbel is a Python package that provides functions for the forward and inverse Abel transforms. The forward Abel transform takes a slice of a cylindrically symmetric 3D object and provides the 2D projection of that object. The inverse Abel transform takes a 2D projection and reconstructs a slice of the cylindrically symmetric 3D distribution.

Inverse Abel transforms play an important role in analyzing the projections of angle-resolved photoelectron/photoion spectra, plasma plumes, flames, and solar occultation.

PyAbel provides efficient implementations of several Abel transform algorithms, as well as related tools for centering images, symmetrizing images, and calculating properties such as the radial intensity distribution and the anisotropy parameters.

Transform Methods

The outcome of the numerical Abel transform depends on the exact method used. So far, PyAbel includes the following transform methods:

1. basex - Gaussian basis set expansion of Dribinski and co-workers.
2. hansenlaw - recursive method of Hansen and Law.
3. direct - numerical integration of the analytical Abel transform equations.
4. two_point - the "two point" method of Dasch and co-workers.
5. three_point - the "three point" method of Dasch and co-workers.
6. onion_peeling - the "onion peeling" deconvolution method of Dasch and co-workers.
7. onion_bordas - "onion peeling" or "back projection" method of Bordas et al. based on the MatLab code by Rallis and Wells et al.
8. linbasex - the 1D-spherical basis set expansion of Gerber et al.
9. rbasex - a pBasex-like method formulated in terms of radial distributions.

Installation

PyAbel requires Python 2.7 or 3.5-3.7. NumPy and SciPy are also required, and Matplotlib is required to run the examples. If you don't already have Python, we recommend an "all in one" Python package such as the Anaconda Python Distribution, which is available for free.

With pip

The latest release can be installed from PyPi with

pip install PyAbel

With setuptools

If you prefer the development version from GitHub, download it here, cd to the PyAbel directory, and use

python setup.py install

Or, if you wish to edit the PyAbel source code without re-installing each time

python setup.py develop

Example of use

Using PyAbel can be simple. The following Python code imports the PyAbel package, generates a sample image, performs a forward transform using the Hansen–Law method, and then a reverse transform using the Three Point method:

import abel
original     = abel.tools.analytical.SampleImage().image
forward_abel = abel.Transform(original, direction='forward', method='hansenlaw').transform
inverse_abel = abel.Transform(forward_abel, direction='inverse', method='three_point').transform

Note: the abel.Transform() class returns a Python class object, where the 2D Abel transform is accessed through the .transform attribute.

The results can then be plotted using Matplotlib:

import matplotlib.pyplot as plt
import numpy as np

fig, axs = plt.subplots(1, 2, figsize=(6, 4))

axs[0].imshow(forward_abel, clim=(0, np.max(forward_abel) * 0.6),
              origin='lower', extent=(-1, 1, -1, 1))
axs[1].imshow(inverse_abel, clim=(0, np.max(inverse_abel) * 0.4),
              origin='lower', extent=(-1, 1, -1, 1))

axs[0].set_title('Forward Abel Transform')
axs[1].set_title('Inverse Abel Transform')

plt.tight_layout()
plt.show()

Output:

Note

Additional examples can be viewed on the PyAbel examples page and even more are found in the PyAbel/examples directory.

Documentation

General information about the various Abel transforms available in PyAbel is available at the links above. The complete documentation for all of the methods in PyAbel is hosted at https://pyabel.readthedocs.io.

Conventions

The PyAbel code adheres to the following conventions:

• Image orientation: PyAbel adopts the "television" convention, where IM[0, 0] refers to the upper left corner of the image. (This means that plt.imshow(IM) should display the image in the proper orientation, without the need to use the origin='lower' keyword.) Image coordinates are in the (row, column) format, consistent with NumPy array indexing, and negative values are interpreted as relative to the end of the corresponding axis. For example, (-1, 0) refers to the lower left corner (last row, 0th column). Cartesian coordinates can also be generated if needed. For example, the x, y grid for a centered 5×5 image:

  x = np.linspace(-2, 2, 5)
  X, Y = np.meshgrid(x, -x)  # notice the minus sign in front of the y coordinate

  The abel.tools.polar.index_coords function does this for images of any shape with any origin.

• Angle: All angles in PyAbel are measured in radians. When an absolute angle is defined, zero angle corresponds to the upwards vertical direction. Positive values are on the right side, and negative values on the left side. The range of angles is from −π to +π. The polar grid for a centered 5×5 image can be generated (following the code above) using

  R = np.sqrt(X**2 + Y**2)
  THETA = np.arctan2(X, Y)

  where the usual (Y, X) convention of arctan2 has been reversed in order to place zero angle in the vertical direction. Consequently, to convert the angular grid back to the Cartesian grid, we use

  X = R * np.sin(THETA)
  Y = R * np.cos(THETA)

  The abel.tools.polar.cart2polar and abel.tools.polar.polar2cart functions are available for conversion between these Cartesian and polar grids.

• Image origin: Fundamentally, the forward and inverse Abel transforms in PyAbel consider the origin of the image to be located in the center of a pixel. This means that, for a symmetric image, the image will have a width that is an odd number of pixels. (The central pixel is effectively "shared" between both halves of the image.) In most situations, the image origin is specified using the origin keyword in abel.Transform (or directly using abel.center.center_image to find the origin (the center of symmetry) of your image). This processing step takes care of shifting the origin of the image to the middle of the central pixel. However, if the individual Abel transforms methods are used directly, care must be taken to supply a properly centered image. Some methods also provide low-level functions for transforming only the right half of the image (with the origin located in the middle of a 0th-column pixel).

• Intensity: The pixel intensities can have any value (within the floating-point range). However, the intensity scale must be linear. Keep in mind that cameras and common image formats often use gamma correction and thus provide data with nonlinear intensity encoding. Thus, if possible, it is recommended to disable the gamma correction on cameras used to record images that will be inverse Abel-transformed. If this is not possible, then it is necessary to apply the appropriate intensity transformations before the analysis. Most PyAbel methods also assume intensities to be floating-point numbers, and when applied to integer types, can return inappropriately rounded results. The abel.Transform class recasts the input image to float64 by default, but if you wish to call the transform methods directly or use other tools, you might need to perform the conversion yourself (as IM.astype(float), for example).

Support

If you have a question or suggestion about PyAbel, the best way to contact the PyAbel Developers Team is to open a new issue.

Contributing

We welcome suggestions for improvement, together with any interesting images that demonstrate application of PyAbel.

Either open a new Issue or make a Pull Request.

CONTRIBUTING.rst has more information on how to contribute, such as how to run the unit tests and how to build the documentation.

License

PyAble is licensed under the MIT license, so it can be used for pretty much whatever you want! Of course, it is provided "as is" with absolutely no warranty.

Citation

First and foremost, please cite the paper(s) corresponding to the implementation of the Abel transform that you use in your work. The references can be found at the links above.

If you find PyAbel useful in you work, it would bring us great joy if you would cite the project. You can find the DOI for the lastest verison here

Additionally, we have written a scientific paper comparing various Abel transform methods. You can find the manuscript at the Review of Scientific Instruments (DOI: doi.org/10.1063/1.5092635) or on arxiv (arxiv.org/abs/1902.09007).

Have fun!