Summary:

We have implemented a concurrent lock free B+Tree (called Palm Tree) that scales to 16 cores, with 60M queries per second (QPS) on read only and R/W mixed workload, which is 15.5x speed up comparing to our single thread implementation. Our implementation can also maintain a nearly linear speed up even for skewed workload.

Backgroud:

B+Tree is intensivily used in database management systems (DBMS). All most all relational database system uses B+Tree as the primary data structure for index. Hence the performance of B+Tree index is critical to fast query performance. On the other hand, there are two hardware trends in recent years for DBMS, systems with high core counts and large memory capacity], which results in the rising of in memory database systems.

The design of B+Tree index data structure of traditional DBMS is far different than that of an in memory database today. Traditional DBMSs assume that the primary storage is on disk (maganetic disk or SSD), and it is fine in most of the case to acquire a latch to provide concurrent accesses to the index because disk IO is anyway slow. However for in main memory DBMS, fetching data from memory is so much faster than from disk, such that the overhead of locking would easily doom the power of underlying hardwares.

In this sense, a high performance concurrent B+Tree is demanded for next generation main memory DBMS. This project is an effort to explore the pallelisim of B+Tree data structures and make it scalable to higher core counts.

A B+Tree is an self balancing tree struture that allows searches, scan, insertions and deletions on key/value pairs. It is a generalization of Binary Search Tree, with the similar concept of internal nodes and leaf nodes. Each inernal node contains a key range, and each range points to a subtree that contains data within that range. Each leaf node contains the actual key/value pairs.

The mechanism of B+Tree’s ability to keep self balanced is to split when a leaf node or internal node becomes too large, and to merge when a node becomes too small. Particularly, when root of a B+Tree splits, a new root will be allocated the tree depth is increased by one, and when the entire layer of the tree merges, the tree node will decsend and the tree depth is decreased by one. The split and merge operations are critical to maintain a balanced tree with similar sized nodes.

To implement a B+Tree, the following or similar operations need to be provided.

• search(key): search for the leaf node that contains key from root to bottom and returns the leaf node.
• add_item(node, key, value): add an item to a node for a given key, the value could either be a child pointer (for internal node), or the actual value (for leaf node). This operation may cause a node to split.
• del_item(node, key): delete an item from a node for a given key. As opposed to add_item(), this operation may cause a node to merge.
• split(node): split a node into multiple nodes, the ranges of the splitted nodes are continuous and the items are sorted within each node. Returns the new nodes that are splitted out. The parents of the spillted node will insert newly created child nodes.
• merge(node): if a node contains few keys, it will be merged. The parents of the merged node will re-insert the merged key/values into other nodes, and reclaim the space of the merged child node.
• handle_root(): this is a special handler of the root node, because the split and merge of the root will cause the tree depth to change, and new root may need to be assigned.

For our prototype system, we implmeneted 3 public APIs in C++:

• bool find(const KeyType &key, ValueType &value). find() will search for key and fill in the corresponding value. It will return true if the key/value pair is found, and false otherwise.
• void delete(const KeyType &key). delete() will delete the entry in the tree if key is present in the tree.
• void insert(const KeyType &key, const ValueType &valuel); insert() will insert an entry into the tree.

###Approach: ####Approach #1: Coarse Grained Locking There are several ways to implement a concurrent B+Tree. The easiest one is to have a coarse grained lock to protect the tree, for example we can use a shared lock to support find(), delete() and insert(). The strategy is simple, find() can take a read lock, as it won’t change the structure of the tree. delete() and insert() need to take a write lock, because it will modify the tree. The advantage of coarse grained locking is its simplism, but it is often not the optimal solution since find() will block delete() and insert(), delete() and insert() will block all other operations on the tree.

####Approach #2: Fine Grained Locking The second approach is to use fine grained locking to protect the tree data structure. One viable way is to use some sort of hand-over-hand locking when searching down the tree, and lock the corresponding nodes before the tree structure is modified. In this project, to compare with our lock free implmenetation, we also designed and implemented a fine grained locking B+Tree:

• For find(), we first acquire a lock on the root node, find the corresponding child node and acquire the lock on that node then release the lock held previously on the root node. For internal node, we always acquire a lock on the target child node before releasing the lock.
• For delete() and insert(), because they will potentially modify its parent node (by splitting or merging), and possibly propagate the tree modifications all the way up to the root node, we decided to acquire a lock on each node along the way we search down the tree, so we are sure that no others are possibly searching or modifying on the path.

The advantage of this approach is that readers will not block readers, and it blocks writers in a fine grained way (unlike the first approach, because search() uses a hand-over-hand locking scheme, the writers may still be able to proceed its operations after a unfinished reader). It is also reasonably simple to implement.

The disadvantage of this approach is that writers will still block readers. The writers will take an exclusive path on the tree, meaning that no other operations are possibly happen at the same time.

####Approach #3: Lock Free Approach #1 and #2 both used lock to protect the data strucutre. In both cases, writers will block readers and other writers. It is more soundable to implement a lock free B+Tree that both readers and writers can proceed without blocking each other. One of such example is Palm Tree. Palm Tree is a lock free concurrent B+Tree proposed by Intel in [1], it features a Bulk Synchronized Parallism (BSP) approach to bulkly perform B+Tree operations and resolve hazards gracefully. The main contribution of this project is an efficient implementation of Palm Tree.

The first idea of Palm Tree is to group quries into batches, and the batches are processed one at a time cooperatively by a pool of threads. The idea behind batch is that by performing more quries at a time will likely to compensate the communication and scheduling overhead.

Second, to resolve conflicting access to the tree, Palm Tree adopts a stage by stage Bulk Synchronize fasion for query processing, that is a batch is processed in different stages on different layers of the tree. Between different stage, there is a synchronization point to make sure that each worker has finished the last stage and is ready for the next stage (it sounds like a barrier, the real implementation might not necessarily be one).

1. Stage 0: In the 0 stage, queries in a batch are evenly assigned to workers

2. Stage 1: Every query requires firstly search down the tree to locate the leaves, the workers in stage 1 perform this search and record the target leaf node for each query.

3. Stage 2: At this stage, insert() or delete() may modify the leaf nodes, to prevent race conditions, these operations are partitioned by nodes, and are re-distributed to worker threads on a node by node base. This redistribution guarantees that each node is only accessed by exactly one worker, so that conflicing accesses are avoided inherently.

   After the redistribution, the workers will execute insert() and delete(). During this process, the workers may generate split and merge requests to parent node. These operations are registered in the upper layer, but is not executed immediately because other siblings may also want to split and merge, causing the parent node being updated concurrently without protection.

4. Stage 3: During this stage, each node gathers split and merge requests from its children. These requests are again grouped by each node (here node is the parent node respective to the node in stage 2) and assigned to workers. Stage 3 may again generate some split and merge requests to its upper layer. We repeat Stage 3 on each layer up to the root node, until then the necessary tree modifications are all done in such manner except the root node.

5. Stage 4: This is the final stage. A single thread will handle the special case of root split and root merge. For a root split, a new root is allocated, it will point to the old root and newly splitted node. For a root merge, we did some trick to merge the root only when the root has one sinlge child, we decsend the root node and use the single child as the new root. In the end of stage 4, all queries in the batch are fullfilled, the results of the batch are finally delivered back to clients.

During the upwards operations, within each layer the task needs to be re-distributed to ensure correctness and leverages parallisms. Palm Tree's partition algorithm is as follows: for each worker thread, it records all the nodes it has accessed in the lower level, then dicards all nodes that have been accessed by a worker with a lower worker id (each worker is assigned a worker id from 0~WORKER_NUM). One drawbacks of such approach would be workload imbalance, as the worker with lower id has privilege over other workers.

###Optimizations:

• The first optimization we made is to pre-sort the queries in a batch, and assign them to threads in an ordered way. We will see below that pre-sort can benifit task distribution process, here the main benift is load balancing. If the batch is pre-sorted, each worker thread will be assigned a range of queries, and they will reach leaf layer with properly ordered leaf nodes. Comparing to random assignment of tasks, the 0th worker may end up with many leaf nodes, potentially have more work than others due to the task distribution policy.

• Next, we soonly find out that memory allocation is a bottleneck. When we measured from perf, with higher thread counts, the time spent in malloc and free takes longer and longer, so we suspuct the memory allocator is not scalable. We searched online and find a good scalable memory allocator called JEMalloc, it is nearly zero change to our code to use JeMalloc.

• SIMD accelearation for key lookup. There are two ways to lookup a key during tree search. If the keys in the node are sorted, we can use binary search to search the key. If the node is not sorted, we can linearly scan and match the keys. While binary search has a better aymptotic complexity than linear scan, it suffers from branch mispredications and requires the keys in the node to be sorted. Linear scan on the other hand, may potentially has the same overhead as binary search given the node size is small, can further exploit SIMD acceleration, and has a fast delete and insert speed as the node is not acquired to be sorted. Using SIMD to linearly search for key seems to be a counter-ituitive but efficient way for key lookups.

• Reduce communication overhead.

  • Pre-sort a batch with different purpose. Task distribution is actually a proactive process. As described in the previous section, task distribution is by probing into other threads' task and determine which tasks belong to the worker, sorting the queries beforehand can potentially just looking at a worker's neighbours.
  • Previously, the 0th worker is a special worker, it is responsible for distributing the queries on the tree to all other workers. This portion of code is sequential, we improve it by let each thread calculate the range of its responsible quries and collect its own task cooperatively.

Results:

The platform we run our evaluation on:

• 18 cores, 36 hardware threads
• 2.9 GHz cpu, 32K L1 cache, 256K L2 cache, 26M L3 cache
• 2 NUMA nodes, 60GB memory

First look at our final evaluation with all optimization implemented. We have evaluated a read only benchmark and a 20% update 80% read mixed benchmark. We pre-poplate the tree with different number of items before generating the workloads.

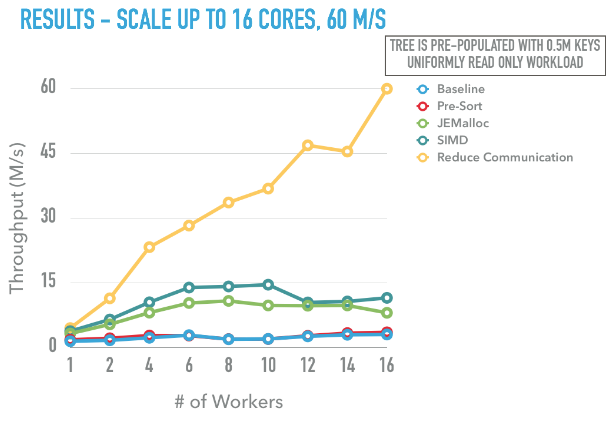
Below is a graph showing different optimization we did towards the final scalable algorithm. The workload used in this graph is a read only workload with uniform access patterns on a tree with 0.5M keys.

The baseline version has a throughput about 2000KQPS, we didn’t see a huge speedup by adapting the pre-sort optimization mentioned in the paper, this is mainly because the system is bottlenecked by the the memory allocator. We then replaced the default libc’s malloc with jemalloc, the performance now greatly goes up, however after 6 cores there is no more throughput gain. The B+tree throughput is 10MQPS. At this point, applying SIMD to the data structure can provide a 10%-20% speed up.

Then the huge performance gain is from reducing the communciation overhead. We first implemented a customized profiler to collect running time of different stages of the system. As can be seen from the log output when profing on 4 workers and 8 workers Palm Tree, we found that batch collection (Stage 0) and result distribution (Stage 4) is not scalable, mainly because it is only done by the 0th worker by design.

I0505 01:02:58.919889 70461 palmtree.h:63] [collect_batch]
I0505 01:02:58.919924 70461 palmtree.h:68] 0: 1.06791      <=
I0505 01:02:58.919939 70461 palmtree.h:68] 1: 0
I0505 01:02:58.919947 70461 palmtree.h:68] 2: 0
...
I0505 01:02:58.920054 70461 palmtree.h:63] [end_stage]
I0505 01:02:58.920061 70461 palmtree.h:68] 0: 1.09612      <=
I0505 01:02:58.920070 70461 palmtree.h:68] 1: 0
I0505 01:02:58.920078 70461 palmtree.h:68] 2: 0
...
I0505 01:02:58.920110 70461 palmtree.h:63] [total_time]
I0505 01:02:58.920117 70461 palmtree.h:68] 0: 3.12207
I0505 01:02:58.920125 70461 palmtree.h:68] 1: 3.12296
I0505 01:02:58.920133 70461 palmtree.h:68] 2: 3.1128
...

To fix this problem, we let each thread calculate its own task ranges in the batch, and fetches the task without communicating with others, and hence there is not 0th worker's responsibility to distribute the batch tasks. When the task is finished, the worker threads are responsible for returning the results back cooperatively, instead of all done by 0th worker.

Another communication overhead is in stage 2's redistribution of node modification tasks, shown in the following screenshot. By pre-sorting the batch, a worker node may be able to only probe its neighbours’ task s to determine its tasks.

As shown in the graph, the final speed up is promising, we have achieved 60M QPS on a 16 core system and the algorithm scales very well!

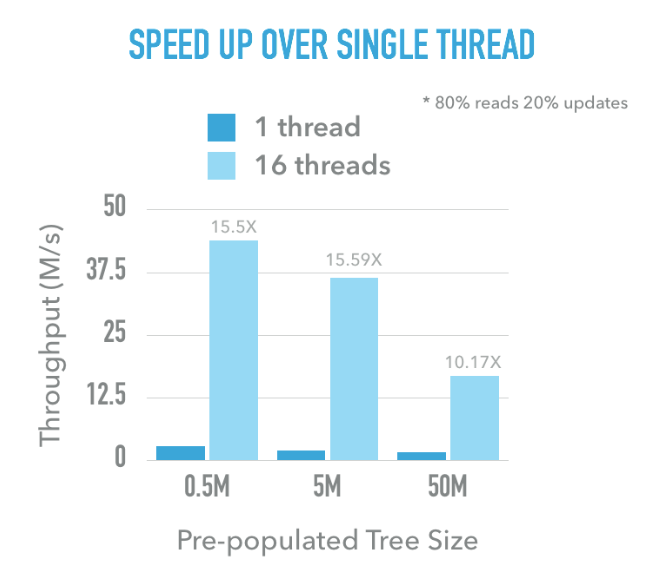
The following graph shows the scalability of our implementation, we vary the number of workers in the worker pool as well as the pre-populated tree’s size. When the tree is of medium or small size, the speed up is close to a linear speed up. When the tree size is large, we believe the system has been memory bounded so that the speed up is not as good (however it is still 10x). This workload is a 20% update, 80% read workload with uniform access to keys in the tree.

Our implmentation is also resilient to skewed data access patterns. The following graph is the comparison of throughput for uniform access and contended access. The contended workload is generated by having 80% of operations accesing 20% of the entries in the tree. For either small, medium or large trees, the throughput has a slightly drop but not much for skewed access, showing that our implementation can actually resist to the skewness quite well.

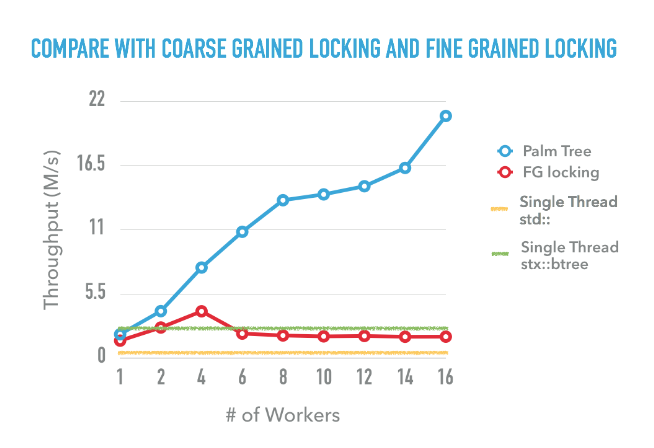
We have also compared the performance of Palm Tree with single thread std::map and single thread stx::btree (an open source efficient implementation of B+Tree), and also our not so efficient implementation of fine grained lock B+Tree in hand-over-hand fasion. As can be seen, std::map is generally not performent even for single thread, stx::btree is performant for single thread but it is not a concurrent data structure. We have tried to add a shared lock to both std::map and stx::btree, it turns out they perform even worse in a many core settings. The hand-over-hand B+Tree can’t scale beyond 4 threads. We wish we would have a better implementation of fine grained locking B+Tree, but it turns out to be even harder than Palm Tree, many corner cases might happen, given limited time we are not able to engage into that.

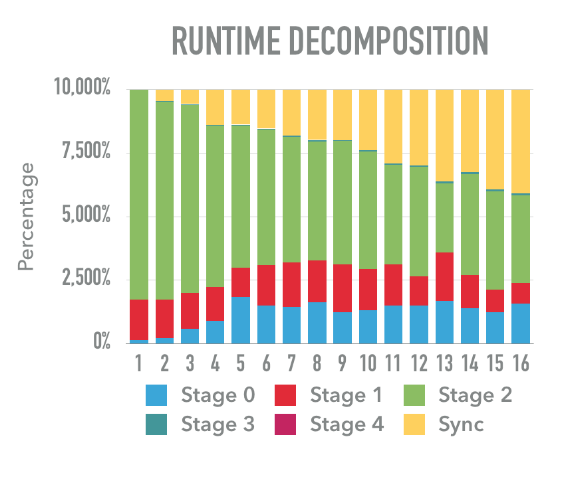
The final graph is about the decomposition of time spent in each stage of a workload. The workload is 20% update, 80% read, 0.5M keys in the tree, uniform access. We generated 1B of operations to the tree.

From the runtime decomposition we can see that the time spent in stage 2 is being less and less significant when more threads are used. Recall that stage 2 is actually matching keys, inserting keys or removing keys on the leaf node, this is one of the most expensive and frequent operations in Palm Tree. in the beginning when there is just one thread, most of the time is spent on stage 2. However with the increasing of number of workers, the communication overhead becomes more and more significant, it grows from nearly 0% for 1 thread to around 33%, for 16 threads. This is not surprising as we have more threads, the more likely that they can’t keep up with each other so that waiting is common. One way to overcome this problem will be focusing on how to elimiate this all to all communications.

References:

[1] J. Sewall, J. Chhugani, C. Kim, N. Satish, and P. Dubey. PALM: Parallel architecture-friendly latch-free modifications to B+ trees on many-core processors. Proc. VLDB Endowment, 4(11):795--806, August 2011.

[2] David B. Lomet, Sudipta Sengupta, and Justin J. Levandoski. 2013. The Bw-Tree: A B-tree for new hardware platforms. In Proceedings of the 2013 IEEE International Conference on Data Engineering (ICDE 2013) (ICDE '13). IEEE Computer Society, Washington, DC, USA, 302-313. DOI=http://dx.doi.org/10.1109/ICDE.2013.6544834

Work Partition:

Equal work was performed by both project members (@Ran Xian and @Runshen Zhu).