Skip to content

Latest commit

 

History

History
2565 lines (1892 loc) · 75 KB

eccc.md

File metadata and controls

2565 lines (1892 loc) · 75 KB
Raw

Table of Contents generated with DocToc

Setup

These notes started few years ago from the official SWC lesson http://swcarpentry.github.io/python-novice-gapminder, but then evolved quite a bit to include other topics. You can find these notes at http://bit.ly/wgeccc.

instructor students
(1) log in to socrative.com as a teacher (1) log in to socrative.com as a student
(2) start a quiz, select 'python quiz' (2) enter provided room name
(3) select 'teacher paced'
(4) disable student names
(5) start

Running Jupyter notebooks

Python pros Python cons
elegant scripting language slow (interpreted, dynamically typed)
powerful, compact constructs for many tasks
very popular across all fields
huge number of external libraries

Python programs are plain text files, stored with the .py extension.

Many ways to run Python commands:

  • from the inside a Unix shell can start a Python shell and type commands
  • running Python scripts saved in *.py files
  • from Jupyter (formerly iPython) notebooks - stored as JSON files, displayed as HTML

Today we will use a Jupyter notebook. You have several options:

  1. if you have a university computer ID, go to https://syzygy.ca and under Launch select your institution, then fill in your credentials
  2. if you have a Google account, go to https://syzygy.ca and under Launch select either Cybera or PIMS, then log in
  3. if you have a GitHub account, go to https://westgrid.syzygy.ca
  4. if you have Python+Jupyter installed locally on your machine, then you can start it locally from your shell by typing jupyter notebook; you will need the following Python packages installed on your computer: numpy, networkx, pandas, scikit-image, matplotlib, xarray, nc-time-axis, cartopy, netcdf (for reading/writing NetCDF files)

This will open a browser page pointing to the Jupyter server (remote except for the last option). Click on New -> Python 3. Explain: tab completion, annotating code, displaying figures inside the notebook.

  • Esc - leave the cell (border becomes blue) to the control mode
  • "A" - insert a cell above the current cell
  • "B" - insert a cell below the current cell
  • "X" - delete the current cell
  • "M" - turn the current cell into the markdown cell
  • "H" - to display help
  • Enter - re-enter the cell (border becomes green) from the control mode
  • can enter Latex equations in a markdown cell, e.g. $int_0^\infty f(x)dx$ 
print(1/2)   # to run all commands in the cell, either use the Run button, or press shift+return

Variables and Assignment

  • possible names for variables
  • don't use built-in function names for variables, e.g. declaring sum won't let you use sum(), same for print
  • Python is case-sensitive
age = 100
firstName = 'Jason'
print(firstName, 'is', age, 'years old')
a = 1; b = 2    # can use ; to separate multiple commands in one line
a, b = 1, 2   # assign variables in a tuple notation; same as last line
a = b = 10    #  assign a value to multiple variables at the same time
b = "now I am a string"    # variables can change their type on the fly
  • variables persist between cells
  • variables must be defined before use
  • variables can be used in calculations
age = age + 3   # another syntax: age += 3
print('age in three years:', age)

Quiz 1: predicting values

With simple variables in Python, assigning var2 = var1 will create a new object in memory var2. Here we have two distinct objects in memory: initial and position.

Note: With more complex objects, its name could be a pointer. E.g. when we study lists, we'll see that initial and new below really point to the same list in memory:

initial = [1,2,3]
new = initial        # create a pointer to the same object
initial.append(4)    # change the original list to [1, 2, 3, 4]
print(new)           # [1, 2, 3, 4]
new = initial[:]     # one way to create a new object in memory
import copy
new = copy.deepcopy(initial)   # another way to create a new object in memory

Use square brackets to get a substring:

element = 'helium'
print(element[0])   # single character
print(element[0:3])   # a substring

Quiz 2: getting the second digit of a number (not a string!)

  • python is case-sensitive
  • use meaningful variable names

Data Types and Type Conversion

print(type(52))
print(type(52.))
print(type('52'))

print(name+' Smith')   # can add strings
print(name*10)         # can replicate strings by mutliplying by a number
print(len(name))       # strings have lengths

print(1+'a')           # cannot add strings and numbers
print(str(1)+'a')   # this works
print(1+int('2'))   # this works

Built-in Functions and Help

  • Python comes with a number of built-in functions
  • a function may take zero or more arguments
print('hello')
print()

print(max(1,2,3,10))
print(min(5,2,10))
print(min('a', 'A', '0'))   # works with characters, the order is (0-9, A-Z, a-z)
print(max(1, 'a'))    # can't compare these
round(3.712)      # to the nearest integer
round(3.712, 1)   # can specify the number of decimal places
help(round)
round?   # Jupyter Notebook's additional syntax
  • every function returns something, whether it is a variable or None
result = print('example')
print('result of print is', result)   # what happened here? Answer: print returns None

Conditionals

Python implements conditionals via if, elif (short for "else if") and else. Use an if statement to control whether some block of code is executed or not.

mass = 3.54
if mass > 3.0:
    print(mass, 'is large')

Let's modify the mass:

mass = 2.07
if mass > 3.0:
    print (mass, 'is large')

Add an else statement:

mass = 2.07
if mass > 3.0:
    print(mass, 'is large')
else:
    print(mass, 'is small')

Add an elif statement:

x = 5
if x > 0:
    print(x, 'is positive')
elif x < 0:
    print(x, 'is negative')
else:
    print(x, 'is zero')

What is the problem with the following code?

grade = 85
if grade >= 70:
    print('grade is C')
elif grade >= 80:
    print('grade is B')
elif grade >= 90:
    print('grade is A')

Lists

A list stores many values in a single structure.

T = [27.3, 27.5, 27.7, 27.5, 27.6]   # array of temperature measurements
print('temperature:', T)
print('length:', len(T))

print('zeroth item of T is', T[0])
print('fourth item of T is', T[4])

T[0] = 21.3
print('temperature is now:', T)

primes = [2, 3, 5]
print('primes is initially', primes)
primes.append(7)   # append at the end
primes.append(11)
print('primes has become', primes)

print('primes before', primes)
del primes[4]   # remove element #4
print('primes after', primes)

a = []   # start with an empty list
a.append('Vancouver')
a.append('Toronto')
a.append('Kelowna')
print(a)

a[99]   # will give an error message (past the end of the array)
a[-1]   # display the last element; what's the other way?
a[:]    # will display all elements
a[1:]   # starting from #1
a[:1]   # ending with but not including #1

Lists can be heterogeneous and nested:

a = [11, 21, 31]
b = ['Mercury', 'Venus', 'Earth']
c = 'hello'
nestedList = [a, b, c]
print(nestedList)

You can search inside a list:

'Venus' in b      # returns True
'Mars' in b       # returns False
b.index('Venus')      # returns 1 (position index)

And you sort lists alphabetically:

b.sort()
b             # returns ['Earth', 'Mercury', 'Venus']

To delete an item from a list:

b.pop(2)             # you can use its index
b.remove('Earth')       # or you can use its value

Exercise: write a script to find the second largest number in the list [77,9,23,67,73,21].

For Loops

For loops are very common in Python and are similar to for in other languages, but one nice twist with Python is that you can iterate over any collection, e.g., a list, a character string, etc.

for number in [2, 3, 5]:    # number is the loop variable; [...] is a collection
    print(number)          # Python uses indentation to show the body of the loop

This is equivalent to:

print(2)
print(3)
print(5)

What will this do:

for number in [2, 3, 5]:
    print(number)
print(number)
  • the loop variable could be called anything
  • the body of a loop can contain many statements
  • use range to iterate over a sequence of numbers
for i in 'hello':
    print(i)

for i in range(0,3):
    print(i)

Let's sum numbers 1 to 10:

total = 0
for number in range(10):
    total = total + (number + 1)   # what's the other way to sum numbers 1 to 10? how about range(1,11)?
print(total)

Quiz 3: revert a string

Exercise: Print a difference between two lists, e.g., [1, 2, 3, 4] and [1, 2, 5].

Exercise: write a script to get the frequency of the elements in a list. You are allowed to google this problem :)

While loops

Since we talk about loops, we should also briefly mention while loops, e.g.

x = 2
while x > 1.:
    x /= 1.1
    print(x)

More on lists in loops

You can also form a zip object of tuples from two lists of the same length:

for i, j in zip(a,b):
    print(i,j)

And you can create an enumerate object from a list:

for i, j in enumerate(b):    # creates a list of tuples with an iterator as the first element
    print(i,j)

List comprehensions

It's a compact way to create new lists based on existing lists/collections. Let's list squares of numbers from 1 to 10:

[x**2 for x in range(1,11)]

Of these, list only odd squares:

[x**2 for x in range(1,11) if x%2==1]

You can also use list comprehensions to combine information from two or more lists:

week = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']
weekend = ['Sat', 'Sun']
print([day for day in week])                         # the entire week
print([day for day in week if day not in weekend])   # only the weekdays
print([day for day in week if day in weekend])       # in both lists

The syntax is:

[something(i) for i in list1 if i [not] in list2 if i [not] in list3 ...]

Quiz 4: sum up squares of numbers

Exercise: Write a script to build a list of words that are shorter than n from a given list of words ['red', 'green', 'white', 'black', 'pink', 'yellow'].

Dictionaries

Lists in Python are ordered sets of objects that you access via their position/index. Dictionaries are unordered sets in which the objects are accessed via their keys. In other words, dictionaries are unordered key-value pairs.

favs = {'mary': 'orange', 'john': 'green', 'eric': 'blue'}
favs
favs['john']      # returns 'green'
favs['mary']      # returns 'orange'
list(favs.values()).index('blue')     # will return the index of the first value 'blue'

for key in favs:
    print(key)          # will print the names	
for k in favs.keys():
    print(k)            # the same
for key in favs:
    print(favs[key])      # will print the colours
for v in favs.values():
    print(v)                   # the same
for i, j in favs.items():
    print(i,j)           # both the names and the colours

Now let's see how to add items to a dictionary:

concepts = {}
concepts['list'] = 'an ordered collection of values'
concepts['dictionary'] = 'a collection of key-value pairs'
concepts

Let's modify values:

concepts['list'] = 'simple: ' + concepts['list']
concepts['dictionary'] = 'complex: ' + concepts['dictionary']
concepts

Deleting dictionary items:

del concepts['list']       # remove the key 'list' and its value

Values can also be numerical:

grades = {}
grades['mary'] = 5
grades['john'] = 4.5
grades

And so can be the keys:

grades[1] = 2
grades

Sorting dictionary items:

favs = {'mary': 'orange', 'john': 'green', 'eric': 'blue', 'jane': 'orange'}
sorted(favs)             # returns the sorted list of keys
sorted(favs.keys())      # the same
sorted(favs.values())         # returns the sorted list of values
for k in sorted(favs):
    print(k, favs[k])          # full dictionary sorted by the key

Exercise: Write a script to print the full dictionary sorted by the value.

Similar to list comprehensions, we can form a dictionary comprehension:

{k:'.'*k for k in range(10)}
{k:v*2 for (k,v) in zip(range(10),range(10))}
{j:c for j,c in enumerate('computer')}

Writing functions

  • functions encapsulate complexity so that we can treat it as a single thing
  • functions enable re-use: write one time, use many times

First define:

def greeting():
    print('Hello!')

and then we can run it:

greeting()

def printDate(year, month, day):
    joined = str(year) + '/' + str(month) + '/' + str(day)
    print(joined)
printDate(1871, 3, 19)

Every function returns something, even if it's None.

a = printDate(1871, 3, 19)
print(a)

How do we actually return a value from a function?

def average(values):   # the argument is a list
    if len(values) == 0:
        return None
    return sum(values) / len(values)
a = average([1, 3, 4])
print('average of actual values:', a)

Quiz 5: convert from Fahrenheit to Celsius

Quiz 6: convert from Celsius to Fahrenheit

Quiz 7: convert temperature lists

Function arguments in Python can take default values becoming optional:

def addNumber(a, b=1):
    return a+b
print(addNumber(5))
print(addNumber(5,3))

With several optional arguments it is important to be able to differentiate them:

def modify(a, b=1, coef=1):
    return a*coef + b
print(modify(10))
print(modify(10, 1))   # which argument did we add?
print(modify(10, coef=2))
print(modify(10, coef=2, b=5))

Any complex python function will have many optional arguments, for example:

?print

Variable scope

The scope of a variable is the part of a program that can see that variable.

a = 5
def adjust(b):
	sum = a + b
    return sum
adjust(10)   # what will be the outcome?
  • "a" is the global variable => visible everywhere
  • "b" and "sum" are local variables => visible only inside the function

Inside a function we can access methods of global variables:

a = []
def add():
    a.append(5)   # modify global `a`
add()
a       # [5]

If we have time

(1) How would you explain the following:

1 + 2 == 3           # returns True (makes sense!)
0.1 + 0.2 == 0.3     # returns False -- be aware of this when you use conditionals
abs(0.1+0.2 - 0.3) < 1.e-8     # compare floats for almost equality
import numpy as np
np.isclose(0.1+0.2, 0.3, atol=1e-8)

(2) More challening: write a code to solve x^3+4x^2-10=0 with a bisection method in the interval [1.3, 1.4] with tolerance 1e-8.

Libraries

Most of the power of a programming language is in its libraries. This is especially true for Python which is an interpreted language and is therefore very slow (compared to compiled languages). However, the libraries are often compiled (can be written in compiled languages such as C/C++) and therefore offer much faster performance than native Python code.

A library is a collection of functions that can be used by other programs. Python's standard library includes many functions we worked with before (print, int, round, ...) and is included with Python. There are many other additional modules in the standard library such as math:

print('pi is', pi)
import math
print('pi is', math.pi)

You can also import math's items directly:

from math import pi, sin
print('pi is', pi)
sin(pi/6)
cos(pi)
help(math)   # help for libraries works just like help for functions
from math import *

You can also create an alias from the library:

import math as m
print m.pi

Quiz 8: exploring the math library

Quiz 9: random numbers

Quiz 10: forgot to load the library

Quiz 11: degree conversion with math

Virtual environments and packaging

To install a package into the current Python environment from inside a Jupyter notebook, simply do:

%pip install packageName

In Python you can create an isolated environment for each project, into which all of its dependencies will be installed. This could be useful if your several projects have very different sets of dependencies. On the computer running your Jupyter notebooks, open the terminal and type:

pip install virtualenv
virtualenv climate   # create a new virtual environment in your current directory
source climate/bin/activate
which python && which pip
pip install numpy ...
pip install ipykernel   # install ipykernel (IPython kernel for Jupyter) into this environment
python -m ipykernel install --user --name=climate   # add your environment to Jupyter
...
deactivate

Quit all your currently running Jupyter notebooks and the Jupyter dashboard. If running on syzygy.ca, logout from your session and then log back in.

Whether running locally or on syzygy.ca, open the notebook dashboard, and one of the options in New below Python 3 should be climate.

To delete the environment, in the terminal type:

jupyter kernelspec list                  # `climate` should be one of them
jupyter kernelspec uninstall climate     # remove your environment from Jupyter
/bin/rm -rf climate

Numpy

As you saw before, Python is not statically typed, i.e. variables can change their type on the fly:

a = 5
a = 'apple'
print(a)

This makes Python very flexible. Out of these variables you form 1D lists, and these can be inhomogeneous:

a = [1, 2, 'Vancouver', ['Earth', 'Moon'], {'list': 'an ordered collection of values'}]
a[1] = 'Sun'
a

Python lists are very general and flexible, which is great for high-level programming, but it comes at a cost. The Python interpreter can't make any assumptions about what will come next in a list, so it treats everything as a generic object with its own type and size. As lists get longer, eventually performance takes a hit.

Python does not have any mechanism for a uniform/homogeneous list, where -- to jump to element #1000 -- you just take the memory address of the very first element and then increment it by (element size in bytes) x 999. Numpy library fills this gap by adding the concept of homogenous collections to python -- numpy.ndarrays -- which are multidimensional, homogeneous arrays of fixed-size items (most commonly numbers).

  1. This brings large performance benefits!
  • no reading of extra bits (type, size, reference count)
  • no type checking
  • contiguous allocation in memory
  1. numpy lets you work with mathematical arrays.

Lists and numpy arrays behave very differently:

a = [1, 2, 3, 4]
b = [5, 6, 7, 8]
a + b              # this will concatenate two lists: [1,2,3,4,5,6,7,8]

import numpy as np
na = np.array([1, 2, 3, 4])
nb = np.array([5, 6, 7, 8])
na + nb            # this will sum two vectors element-wise: array([6,8,10,12])
na * nb            # element-wise product

Working with mathematical arrays in numpy

Numpy arrays have the following attributes:

  • ndim = the number of dimensions
  • shape = a tuple giving the sizes of the dimensions
  • size = the total number of elements
  • dtype = the data type
  • itemsize = the size (bytes) of individual elements
  • nbytes = the total memory (bytes) occupied by the ndarray
  • strides = tuple of bytes to step in each dimension when traversing an array
  • data = memory address of the array
a = np.arange(10)      # 10 integer elements 0..9
a.ndim      # 1
a.shape     # (10,)
a.nbytes    # 80
a.dtype     # dtype('int64')
b = np.arange(10, dtype=np.float)
b.dtype     # dtype('float64')

In numpy there are many ways to create arrays:

np.arange(11,20)               # 9 integer elements 11..19
np.linspace(0, 1, 100)         # 100 numbers uniformly spaced between 0 and 1 (inclusive)
np.linspace(0, 1, 100).shape
np.zeros(100, dtype=np.int)    # 1D array of 100 integer zeros
np.zeros((5, 5), dtype=np.float64)     # 2D 5x5 array of floating zeros
np.ones((3,3,4), dtype=np.float64)     # 3D 3x3x4 array of floating ones
np.eye(5)            # 2D 5x5 identity/unit matrix (with ones along the main diagonal)

You can create random arrays:

np.random.randint(0, 10, size=(4,5))    # 4x5 array of random integers in the half-open interval [0,10)
np.random.random(size=(4,3))            # 4x3 array of random floats in the half-open interval [0.,1.)
np.random.rand(3, 3)       # 3x3 array drawn from a uniform [0,1) distribution
np.random.randn(3, 3)      # 3x3 array drawn from a normal (Gaussian with x0=0, sigma=1) distribution

Indexing, slicing, and reshaping

For 1D arrays:

a = np.linspace(0,1,100)
a[0]        # first element
a[-2]       # 2nd to last element
a[5:12]     # values [5..12), also a numpy array
a[5:12:3]   # every 3rd element in [5..12), i.e. elements 5,8,11
a[::-1]     # array reversed

Similar for multi-dimensional arrays:

b = np.reshape(np.arange(100),(10,10))      # form a 10x10 array from 1D array
b[0:2,1]      # first two rows, second column
b[:,-1]       # last column
b[5:7,5:7]    # 2x2 block

a = np.array([1, 2, 3, 4])
b = np.array([4, 3, 2, 1])
np.vstack((a,b))   # stack them vertically into a 2x4 array (use a,b as rows)
np.hstack((a,b))   # stack them horizontally into a 1x8 array
np.column_stack((a,b))    # use a,b as columns

Vectorized functions on array elements (aka universal functions = ufunc)

One of the big reasons for using numpy is so you can do fast numerical operations on a large number of elements. The result is another ndarray. In many calculations you can use replace the usual for/while loops with functions on numpy elements.

a = np.arange(100)
a**2          # each element is a square of the corresponding element of a
np.log10(a+1)     # apply this operation to each element
(a**2+a)/(a+1)    # the result should effectively be a floating-version copy of a
np.arange(10) / np.arange(1,11)  # this is np.array([ 0/1, 1/2, 2/3, 3/4, ..., 9/10 ])

Exercise: Let's verify the equation using summation of elements of an ndarray.

Hint: Start with the first 10 terms k = np.arange(1,11). Then try the first 30 terms.

An extremely useful feature of ufuncs is the ability to operate between arrays of different sizes and shapes, a set of operations known as broadcasting.

a = np.array([0, 1, 2])    # 1D array
b = np.ones((3,3))         # 2D array
a + b          # `a` is stretched/broadcast across the 2nd dimension before addition;
               # effectively we add `a` to each row of `b`

In the following example both arrays are broadcast from 1D to 2D to match the shape of the other:

a = np.arange(3)                     # 1D row;                a.shape is (3,)
b = np.arange(3).reshape((3,1))      # effectively 1D column; b.shape is (3, 1)
a + b                                # the result is a 2D array!

Numpy's broadcast rules are:

  1. the shape of an array with fewer dimensions is padded with 1's on the left
  2. any array with shape equal to 1 in that dimension is stretched to match the other array's shape
  3. if in any dimension the sizes disagree and neither is equal to 1, an error is raised
Example 1:
==========
a: (2,3)  ->  (2,3)  ->  (2,3)
b: (3,)   ->  (1,3)  ->  (2,3)
                                ->  (2,3)

Example 2:
==========
a: (3,1)  ->  (3,1)  ->  (3,3)
b: (3,)   ->  (1,3)  ->  (3,3)
                                ->  (3,3)

Example 3:
==========
a: (3,2)  ->  (3,2)  ->  (3,2)
b: (3,)   ->  (1,3)  ->  (3,3)
                                ->  error
"ValueError: operands could not be broadcast together with shapes (3,2) (3,)"

Note on numpy speed: As chance would have it, last week I was working with a spherical dataset describing Earth's mantle convection. It is on a spherical grid with 13e6 grid points. For each grid point, I was converting from the spherical (lateral - radial - longitudinal) velocity components to the Cartesian velocity components. For each point this is a matrix-vector multiplication. Doing this by hand with Python's for loops would take many hours for 13e6 points. I used numpy to vectorize in one dimension, and that cut the time to ~5 mins. At first glance, a more complex vectorization would not work, as numpy would have to figure out which dimension goes where. Writing it carefully and following the broadcast rules I made it work, with the correct solution at the end -- while the total compute time went down to a few seconds!

Let's use broadcasting to plot a 2D function with matplotlib:

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,12))
x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 50).reshape(50,1)
z = np.sin(x)**8 + np.cos(5+x*y)*np.cos(x)    # broadcast in action!
plt.imshow(z)
plt.colorbar(shrink=0.8)

Exercise: Use numpy broadcasting to build a 3D array from three 1D ones.

Aggregate functions

Aggregate functions take an ndarray and reduce it along one (or more) axes. E.g., in 1D:

a = np.linspace(1, 2, 100)
a.mean()     # arithmetic mean
a.max()      # maximum value
a.argmax()   # index of the maximum value
a.sum()      # sum of all values
a.prod()     # product of all values

Or in 2D:

b = np.arange(25).reshape(5,5)
>>> b.sum()
300
b.sum(axis=0)   # add rows
b.sum(axis=1)   # add columns

Boolean indexing

a = np.linspace(1, 2, 100)
a < 1.5
a[a < 1.5]    # will only return those elements that meet the condition
a[a < 1.5].shape
a.shape

More numpy functionality

Numpy provides many standard linear algebra algorithms: matrix/vector products, decompositions, eigenvalues, solving linear equations, e.g.

a = np.array([[3,1], [1,2]])
b = np.array([9,8])
x = np.linalg.solve(a, b)
x
np.allclose(np.dot(a, x),b)    # check the solution

External packages built on top of numpy

A lot of other packages are built on top of numpy. E.g., there is a Python package for analysis and visualization of 3D multi-resolution volumetric data called yt which is based on numpy. Check out this visualization produced with yt.

Many image-processing libraries use numpy data structures underneath, e.g.

import skimage.io        # scikit-image is a collection of algorithms for image processing
image = skimage.io.imread(fname="https://raw.githubusercontent.com/razoumov/publish/master/grids.png")
image.shape       # it's a 1024^2 image, with (R,G,B,\alpha) channels

Let's plot this image using matplotlib:

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.imshow(image[:,:,2], interpolation='nearest')
plt.colorbar(orientation='vertical', shrink=0.75, aspect=50)

Using numpy, you can easily manipulate pixels:

image[:,:,2] = 255 - image[:,:,2]

and then rerun the previous (matplotlib) cell.

Another example of a package built on top of numpy is pandas, for working with 2D tables. Going further, xarray was built on top of both numpy and pandas.

Plotting with matplotlib

Simple line/scatter plots

One of the most widely used Python plotting libraries is matplotlib. Matplotlib is open source and produces static images.

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
from numpy import linspace, sin
x = linspace(0.01,1,300)
y = sin(1/x)
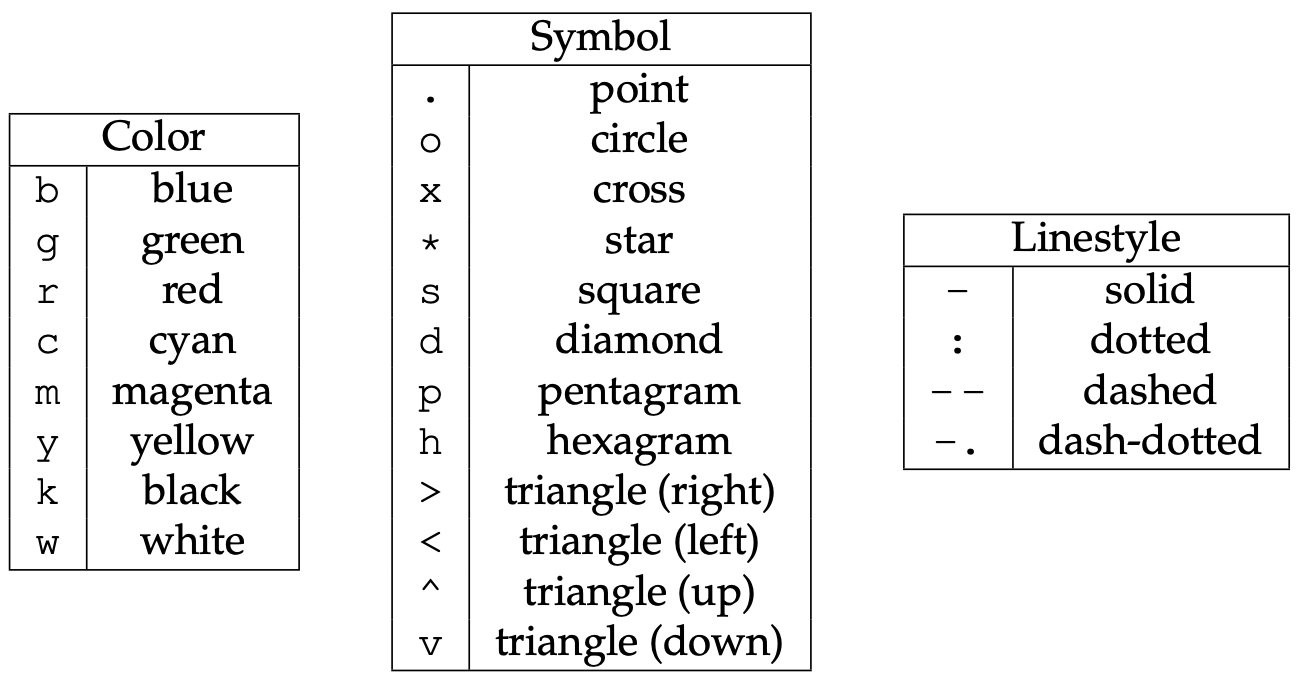
plt.plot(x, y, 'bo-')
plt.xlabel('x', fontsize=18)
plt.ylabel('f(x)', fontsize=18)
# plt.show()       # not needed inside the Jupyter notebook
# plt.savefig('tmp.png')

Let's add the second line, the labels, and the legend. Note that matplotlib automatically adjusts the axis ranges to fit both plots:

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
from numpy import linspace, sin
x = linspace(0.01,1,300)
y = sin(1/x)
plt.plot(x, y, 'bo-', label='one')
plt.plot(x+0.3, 2*sin(10*x), 'r-', label='two')
plt.legend(loc='lower right')
plt.xlabel('x', fontsize=18)
plt.ylabel('f(x)', fontsize=18)

Let's plot these two functions side-by-side:

%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,4))
from numpy import linspace, sin
x = linspace(0.01,1,300)
y = sin(1/x)

ax = fig.add_subplot(121)   # on 1x2 layout create plot #1 (`axes` object with some data space)
a1 = plt.plot(x, y, 'bo-', label='one')
ax.set_ylim(-1.5, 1.5)
plt.xlabel('x')
plt.ylabel('f1')

ax = fig.add_subplot(122)   # on 1x2 layout create plot #2
a2 = plt.plot(x+0.2, 2*sin(10*x), 'r-', label='two')
plt.xlabel('x')
plt.ylabel('f2')

Instead of indices, we could specify the absolute coordinates of each plot with fig.add_axes():

  1. adjust the size fig = plt.figure(figsize=(12,4))
  2. replace the first fig.add_subplot with ax = fig.add_axes([0.1, 0.7, 0.8, 0.3]) # left, bottom, width, height
  3. replace the second fig.add_subplot with ax = fig.add_axes([0.1, 0.2, 0.8, 0.4]) # left, bottom, width, height

The 3rd option is plt.axes() -- it creates an axes object (a region of the figure with some data space). These two lines are equivalent - both create a new figure with one subplot:

fig = plt.figure(figsize=(8,8)); ax = fig.add_subplot(111)
fig = plt.figure(figsize=(8,8)); ax = plt.axes()

Exercise: break the plot into two subplots, the fist taking 1/3 of the space on the left, the second one 2/3 of the space on the right.

Let's plot a simple line in the x-y plane:

import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
x = np.linspace(0,1,100)
plt.plot(2*np.pi*x, x, 'b-')
plt.xlabel('x')
plt.ylabel('f1')

Replace ax = fig.add_subplot(111) with ax = fig.add_subplot(111, projection='polar'). Now we have a plot in the phi-r plane, i.e. in polar coordinates. Phi goes [0,2\pi], whereas r goes [0,1].

?fig.add_subplot    # look into `projection` parameter

import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection='mollweide')
x = np.radians([30,40, 50])
y = np.radians([15, 16, 17])
plt.plot(x, y, 'bo-')

Later, we'll learn how to use this projection parameter with cartopy to map your 2D data from one projection to another.

Let's try a scatter plot:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(10,8))
x = np.random.random(size=1000)   # 1D array of 1000 random numbers in [0.,1.]
y = np.random.random(size=1000)
size = 1 + 50*np.random.random(size=1000)
plt.scatter(x, y, s=size, color='lightblue')

For other plot types click on any example in the Matplotlib gallery.

For colours, see Choosing Colormaps in Matplotlib.

Heatmaps

Let's plot a heatmap of monthly temperatures at the South Pole:

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
plt.figure(figsize=(15,10))

months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec', 'Year']
recordHigh = [-14.4,-20.6,-26.7,-27.8,-25.1,-28.8,-33.9,-32.8,-29.3,-25.1,-18.9,-12.3,-12.3]
averageHigh = [-26.0,-37.9,-49.6,-53.0,-53.6,-54.5,-55.2,-54.9,-54.4,-48.4,-36.2,-26.3,-45.8]
dailyMean = [-28.4,-40.9,-53.7,-57.8,-58.0,-58.9,-59.8,-59.7,-59.1,-51.6,-38.2,-28.0,-49.5]
averageLow = [-29.6,-43.1,-56.8,-60.9,-61.5,-62.8,-63.4,-63.2,-61.7,-54.3,-40.1,-29.1,-52.2]
recordLow = [-41.1,-58.9,-71.1,-75.0,-78.3,-82.8,-80.6,-79.3,-79.4,-72.0,-55.0,-41.1,-82.8]

vlabels = ['record high', 'average high', 'daily mean', 'average low', 'record low']

Z = np.stack((recordHigh,averageHigh,dailyMean,averageLow,recordLow))
plt.imshow(Z, cmap=cm.winter)
plt.colorbar(orientation='vertical', shrink=0.45, aspect=20)
plt.xticks(range(13), months, fontsize=15)
plt.yticks(range(5), vlabels, fontsize=12)
plt.ylim(-0.5, 4.5)

for i in range(len(months)):
    for j in range(len(vlabels)):
        text = plt.text(i, j, Z[j,i],
                       ha="center", va="center", color="w", fontsize=14, weight='bold')

Exercise: Change the text colour to black in the brightest (green) rows and columns. You can do this either by specifying rows/columns explicitly, or (better) by setting a threshold background colour.

Exercise: Modify the code to display only 4 seasons instead of the individual months.

3D topographic elevation

For this we need a data file -- let's download it. Open a terminal inside your Jupyter dashboard. Inside the terminal, type:

wget http://bit.ly/pythfiles -O pfiles.zip
unzip pfiles.zip && rm pfiles.zip        # this should unpack into the directory data-python/

You can now close the terminal panel. Let's switch back to our Python notebook and check our location:

%pwd       # simply run a bash command with a prefix
%ls        # make sure you see data-python/

Let's plot tabulated topographic elevation data:

~~~ {.python}
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

table = pd.read_csv('data-python/mt_bruno_elevation.csv')
z = np.array(table)
nrows, ncols = z.shape
x = np.linspace(0,1,ncols)
y = np.linspace(0,1,nrows)
x, y = np.meshgrid(x, y)
ls = LightSource(270, 45)
rgb = ls.shade(z, cmap=cm.gist_earth, vert_exag=0.1, blend_mode='soft')

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'), figsize=(10,10))    # figure with one subplot
ax.view_init(20, 30)      # (theta, phi) viewpoint
surf = ax.plot_surface(x, y, z, facecolors=rgb, linewidth=0, antialiased=False, shade=False)

Exercise: replace fig, ax = plt.subplots() with fig = plt.figure() followed by ax = fig.add_subplot(). Don't forget about the 3d projection.

Let's replace the last two lines with (running this takes ~10s on my laptop):

ax.view_init(20, 30)
surf = ax.plot_surface(x, y, z, facecolors=rgb, linewidth=0, antialiased=False, shade=False)
for angle in range(90):
    print(angle)
    ax.view_init(20, 30+angle)
    plt.savefig('frame%04d'%(angle)+'.png')

And then we can create a movie in bash:

ffmpeg -r 30 -i frame%04d.png -c:v libx264 -pix_fmt yuv420p -vf "scale=trunc(iw/2)*2:trunc(ih/2)*2" spin.mp4

3D parametric plot

Here is something visually very different, still using ax.plot_surface():

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
from numpy import pi, sin, cos, mgrid

dphi, dtheta = pi/250, pi/250    # 0.72 degrees
[phi, theta] = mgrid[0:pi+dphi*1.5:dphi, 0:2*pi+dtheta*1.5:dtheta]
        # define two 2D grids: both phi and theta are (252,502) numpy arrays
r = sin(4*phi)**3 + cos(2*phi)**3 + sin(6*theta)**2 + cos(6*theta)**4
x = r*sin(phi)*cos(theta)   # x is also (252,502)
y = r*cos(phi)              # y is also (252,502)
z = r*sin(phi)*sin(theta)   # z is also (252,502)

ls = LightSource(270, 45)
rgb = ls.shade(z, cmap=cm.gist_earth, vert_exag=0.1, blend_mode='soft')

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'), figsize=(10,10))
ax.view_init(20, 30)
surf = ax.plot_surface(x, y, z, facecolors=rgb, linewidth=0, antialiased=False, shade=False)

Multidimensional labeled arrays and datasets with xarray

Xarray library is built on top of numpy and pandas, and it brings the power of pandas to multidimensional arrays. There are two main data structures in xarray:

  • xarray.DataArray is a fancy, labelled version of numpy.ndarray
  • xarray.Dataset is a collection of multiple xarray.DataArray's that share dimensions

Data array: simple example from scratch

import xarray as xr
import numpy as np
import pandas as pd
data = xr.DataArray(
    np.random.random(size=(4,3)),
    dims=("y","x"),  # dimension names (row,col); we want `y` to represent rows and `x` columns
    coords={"x": [10,11,12], "y": [10,20,30,40]}  # coordinate labels/values
)
data

We can access various attributes of this array:

data.values                 # the 2D numpy array
data.values[0,0] = 0.53     # can modify in-place
data.dims                   # ('y', 'x')
data.coords               # all coordinates, cannot modify!
data.coords['x'][1]       # a number
data.x[1]                 # the same

Let's add some arbitrary metadata:

data.attrs = {"author": "AR", "date": "2020-08-26"}
data.attrs["name"] = "density"
data.attrs["units"] = "g/cm^3"
data.x.attrs["units"] = "cm"
data.y.attrs["units"] = "cm"
data.attrs    # all attributes
data          # all attributes show here as well
data.x        # only `x` attributes

Subsetting arrays

We can subset using the usual Python square brackets:

data[0,:]     # first row
data[:,-1]    # last column

In addition, xarray provides these functions:

  • isel() selects by index, could be replaced by [index1] or [index1,...]
  • sel() selects by value
  • interp() interpolates by value
data.isel()      # same as `data`
data.isel(y=1)   # second row
data.isel(y=0, x=[-2,-1])    # first row, last two columns
data.x.dtype     # it is integer
data.sel(x=10)   # certain value of `x`
data.y   # array([10, 20, 30, 40])
data.sel(y=slice(15,30))   # only values with 15<=y<=30 (two rows)

There are aggregate functions, e.g.

meanOfEachColumn = data.mean(dim='y')    # apply mean over y
spatialMean = data.mean()
spatialMean = data.mean(dim=['x','y'])   # same

Finally, we can interpolate:

data.interp(x=10.5, y=10)    # first row, between 1st and 2nd columns
data.interp(x=10.5, y=15)    # between 1st and 2nd rows, between 1st and 2nd columns
?data.interp                 # can use different interpolation methods

Plotting

Matplotlib is integrated directly into xarray:

data.plot(size=8)                         # 2D heatmap
data.isel(x=0).plot(marker="o", size=8)   # 1D line plot

Vectorized operations

You can perform element-wise operations on xarray.DataArray like with numpy.ndarray:

data + 100      # element-wise like numpy arrays
(data - data.mean()) / data.std()    # normalize the data
data - data[0,:]      # use numpy broadcasting => subtract first row from all rows

Split your data into multiple independent groups

data.groupby("x")   # 3 groups with labels 10, 11, 12
data.groupby("x").map(lambda v: v-v.min())   # apply separately to each group
            # from each column (fixed x) subtract the smallest value in that column

Dataset: simple example from scratch

Let's initialize two 2D arrays with the identical dimensions:

coords = {"x": np.linspace(0,1,5), "y": np.linspace(0,1,5)}
temp = xr.DataArray(      # first 2D array
    20 + np.random.randn(5,5),
    dims=("y","x"),
    coords=coords
)
pres = xr.DataArray(       # second 2D array
    100 + 10*np.random.randn(5,5),
    dims=("y","x"),
    coords=coords
)

From these we can form a dataset:

ds = xr.Dataset({"temperature": temp, "pressure": pres,
                 "bar": ("x", 200+np.arange(5)), "pi": np.pi})
ds

As you can see, ds includes two 2D arrays on the same grid, one 1D array on x, and one number:

ds.temperature   # 2D array
ds.bar           # 1D array
ds.pi            # one element

Subsetting works the usual way:

ds.sel(x=0)     # each 2D array becomes 1D array, the 1D array becomes a number, plus a number
ds.temperature.sel(x=0)     # 'temperature' is now a 1D array
ds.temperature.sel(x=0.25, y=0.5)     # one element of `temperature`

We can save this dataset to a file:

%pip install netcdf4
ds.to_netcdf("test.nc")
new = xr.open_dataset("test.nc")   # try reading it

We can even try opening this 2D dataset in ParaView - select (x,y) and deselect Spherical.

Exercise: Recall the 2D function we plotted when we were talking about numpy's array broadcasting. Let's scale it to a unit square x,y∈[0,1]:

x = np.linspace(0, 1, 50)
y = np.linspace(0, 1, 50).reshape(50,1)
z = np.sin(5*x)**8 + np.cos(5+25*x*y)*np.cos(5*x)

This is will our image at z=0. Then rotate this image 90 degrees (e.g. flip x and y), and this will be our function at z=1. Now interpolate linearly between z=0 and z=1 to build a 3D function in the unit cube x,y,z∈[0,1]. Check what the function looks like at intermediate z. Write out a NetCDF file with the 3D function.

Time series data

In xarray you can work with time-dependent data. Xarray accepts pandas time formatting, e.g. pd.to_datetime("2020-09-10") would produce a timestamp. To produce a time range, we can use:

import pandas as pd
time = pd.date_range("2000-01-01", freq="D", periods=365*3+1)    # 2000-Jan to 2002-Dec (3 full years)
time
time.month    # same length (1096), but each element is replaced by the month number
time.day      # same length (1096), but each element is replaced by the day-of-the-month
?pd.date_range

Using this time construct, let's initialize a time-dependent dataset that contains a scalar temperature variable (no space) mimicking seasonal change. We can do this directly without initializing an xarray.DataArray first -- we just need to specify what this temperature variable depends on:

import xarray as xr
import numpy as np
ntime = len(time)
temp = 10 + 5*np.sin((250+np.arange(ntime))/365.25*2*np.pi) + 2*np.random.randn(ntime)
ds = xr.Dataset({ "temperature": ("time", temp),        # it's 1D function of time
                  "time": time })
ds.temperature.plot(size=8)

We can do the usual subsetting:

ds.isel(time=100)   # 101st timestep
ds.sel(time="2002-12-22")

Time dependency in xarray allows resampling with a different timestep:

ds.resample(time='7D')    # 1096 times -> 157 time groups
weekly = ds.resample(time='7D').mean()     # compute mean for each group
weekly.temperature.plot(size=8)

Now, let's combine spatial and time dependency and construct a dataset containing two 2D variables (temperature and pressure) varying in time. The time dependency is baked into the coordinates of these xarray.DataArray's and should come before the spatial coordinates:

time = pd.date_range("2020-01-01", freq="D", periods=91) # January - March 2020
ntime = len(time)
n = 100      # spatial resolution in each dimension
axis = np.linspace(0,1,n)
X, Y = np.meshgrid(axis,axis)   # 2D Cartesian meshes of x,y coordinates
initialState = (1-Y)*np.sin(np.pi*X) + Y*(np.sin(2*np.pi*X))**2
finalState =   (1-X)*np.sin(np.pi*Y) + X*(np.sin(2*np.pi*Y))**2
f = np.zeros((ntime,n,n))
for t in range(ntime):
    z = (t+0.5) / ntime   # dimensionless time from 0 to 1
    f[t,:,:] = (1-z)*initialState + z*finalState

coords = {"time": time, "x": axis, "y": axis}
temp = xr.DataArray(
    20 + f,       # this 2D array varies in time from initialState to finalState
    dims=("time","y","x"),
    coords=coords
)
pres = xr.DataArray(   # random 2D array
    100 + 10*np.random.randn(ntime,n,n),
    dims=("time","y","x"),
    coords=coords
)
ds = xr.Dataset({"temperature": temp, "pressure": pres})
ds.sel(time="2020-03-15").temperature.plot(size=8)   # temperature distribution on a specific date
ds.to_netcdf("evolution.nc")

The file evolution.nc should be 100^2 x 2 variables x 8 bytes x 91 steps = 14MB. We can load it into ParaView and play back the pressure and temperature!

Adhering to climate and forecast (CF) NetCDF convention in spherical geometry

So far we've been working with datasets in Cartesian coordinates. How about spherical geometry -- how do we initialize and store a dataset in spherical coordinates (longitude - latitude - elevation)? Very easy: define these coordinates and your data arrays on top, put everything into an xarray dataset, and then specify the following units:

ds.lat.attrs["units"] = "degrees_north"   # this line is important to adhere to CF convention
ds.lon.attrs["units"] = "degrees_east"    # this line is important to adhere to CF convention

Exercise: Let's do it! Create a small (one-degree horizontal + some vertical resolution), stationary (no time dependency) dataset in spherical geometry with one 3D variable and write it to spherical.nc. Load it into ParaView to make sure the geometry is spherical.

Working with atmospheric data

I took one of the ECCC historical model datasets (contains only the near-surface air temperature) published on the CMIP6 Data-Archive and reduced its size picking only a subset of timesteps:

import xarray as xr
data = xr.open_dataset('/Users/razoumov/tmp/xarray/atmosphere/tas_Amon_CanESM5_historical_r1i1p2f1_gn_185001-201412.nc')
data.sel(time=slice('2001', '2020')).to_netcdf("tasReduced.nc")   # last 168 steps

Let's download this file in the terminal:

wget http://bit.ly/atmosdata -O tasReduced.nc

First, quickly check this dataset in ParaView (use Dimensions = (lat,lon)).

data = xr.open_dataset('tasReduced.nc')
data   # this is a time-dependent 2D dataset: print out the metadata, coordinates, data variables
data.time   # time goes monthly from 2001-01-16 to 2014-12-16
data.tas    # metadata for the data variable (time: 168, lat: 64, lon: 128)
data.tas.shape      # (168, 64, 128) = (time, lat, lon)
data.height         # at the fixed height=2m

These five lines all produce the same result:

data.tas[0] - 273.15   # take all values in the second and third dims, convert to Celsius
data.tas[0,:] - 273.15
data.tas[0,:,:] - 273.15
data.tas.isel(time=0) - 273.15
air = data.tas.sel(time='2001-01-16') - 273.15

These two lines produce the same result (1D vector of temperatures as a function of longitude):

data.tas[0,5]
data.tas.isel(time=0, lat=5)

Check temperature variation in the last step:

air = data.tas.isel(time=-1) - 273.15   # last timestep, to celsius
air.shape    # (64, 128)
air.min(), air.max()   # -43.550903, 36.82956

Selecting data is slightly more difficult with approximate floating coordinates:

data.tas.lat
data.tas.lat.dtype
data.tas.isel(lat=0)    # the first value lat=-87.86
data.lat[0]   # print the first latitude and try to use it below
data.tas.sel(lat=-87.86379884)    # does not work due to floating precision
data.tas.sel(lat=data.lat[0])     # this works
latSlice = data.tas.sel(lat=slice(-90,-80))    # only select data in a slice lat=[-90,-80]
latSlice.shape    # (168, 3, 128) - 3 latitudes in this slice

Multiple ways to select time:

data.time[-10:]   # last ten times
air = data.tas.sel(time='2014-12-16') - 273.15    # last date
air = data.tas.sel(time='2014') - 273.15    # select everything in 2014
air.shape     # 12 steps
air.time
air = data.tas.sel(time='2014-01') - 273.15    # select everything in January 2014

Aggregate functions:

meanOverTime = data.tas.mean(dim='time') - 273.15
meanOverSpace = data.tas.mean(dim=['lat','lon']) - 273.15     # mean over space for each timestep
meanOverSpace.shape     # time series (168,)
meanOverSpace.plot(marker="o", size=8)     # calls matplotlib.pyplot.plot

Interpolate to a specific location:

victoria = data.tas.interp(lat=48.43, lon=360-123.37)
victoria.shape   # (168,) only time
victoria.plot(marker="o", size=8)      # simple 1D plot
victoria.sel(time=slice('2001','2020')).plot(marker="o", size=8)   # zoom in on the 21st-century points, see seasonal variations

Let's plot in 2D:

air = data.tas.isel(time=-1) - 273.15   # last timestep
air.time
air.plot(size=8)     # 2D plot, very poor resolution (lat: 64, lon: 128)
air.plot(size=8, y="lon", x="lat")     # can specify which axis is which

What if we have time-dependency in the plot?

a = data.tas[-6:] - 273.15      # last 6 timesteps => 3D dataset => which coords to use for what?
a.plot(x="lon", y="lat", col="time", col_wrap=3)

Breaking into groups and applying a function to each group:

len(data.time)     # 168 steps
data.tas.groupby("time")   # 168 groups
def standardize(x):
    return (x - x.mean()) / x.std()
standard = data.tas.groupby("time").map(standardize)   # apply this function to each group
standard.shape    # (1980, 64, 128) same shape as the original but now normalized over each group

Plotting with cartopy

Cartopy lets you process your geospatial data in order to produce maps, e.g. using various map projections. All plotting is still being done by Matplotlib.

import cartopy.crs as ccrs
import matplotlib.pyplot as plt
import cartopy.feature as cfeature
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection=ccrs.PlateCarree())
ax.coastlines()
ax.coastlines(resolution='50m', color='gray', linewidth=2)   # valid scales are "110m", "50m", "10m"
ax.add_feature(cfeature.OCEAN)
ax.add_feature(cfeature.LAND)
ax.add_feature(cfeature.BORDERS, linestyle=':')

Try the following projections (and bring online help on these):

  • PlateCarree(0) is the equi-rectangular/Cartesian projection (meridians are vertical straight lines)
  • Orthographic(-100,55)
  • Mollweide(0)
  • Robinson(0)
  • InterruptedGoodeHomolosine(0)

More information on cartopy projections.

Let's only plot North America:

fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection=ccrs.Mollweide(-100))
ax.coastlines()
ax.add_feature(cfeature.OCEAN)
ax.add_feature(cfeature.LAND)
ax.add_feature(cfeature.BORDERS, linestyle=':')
ax.set_extent([-160, -51, 5, 85])

You can zoom in much further, and the high-resolution data will be downloaded from online sources. E.g. let's focus on Vancouver Island:

fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, projection=ccrs.PlateCarree())
ax.coastlines()
ax.add_feature(cfeature.OCEAN)
ax.add_feature(cfeature.LAND)
ax.add_feature(cfeature.BORDERS, linestyle=':')
ax.set_extent([-129, -122, 46, 53])

Let's overlay the Natural Earth shaded relief on top of our map and display the night shade:

fig = plt.figure(figsize=(14,12))
ax = fig.add_subplot(111, projection=ccrs.Mollweide())
ax.stock_img()   # add the Natural Earth shaded relief image
ax.add_feature(cfeature.BORDERS, linestyle=':')

import datetime
import pytz
date = datetime.datetime.now()   # local time now
utc = datetime.datetime.utcnow()   # UTC time now
date, utc

from cartopy.feature.nightshade import Nightshade
ax.add_feature(Nightshade(utc, alpha=0.2))

Let's plot 1D data (a line connecting two points on top of our map):

import cartopy.crs as ccrs
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(12,12))
ax = plt.axes(projection=ccrs.Robinson(-150))
ax.stock_img()

vancouver = (-123.12, 49.28)
perth = (115.86, -31.95)

lon = [vancouver[0], perth[0]]
lat = [vancouver[1], perth[1]]

plt.plot(lon, lat, color='blue', linewidth=2, marker='o')   # does not work!

We need to tell matplotlib that our line is a straight line in spherical geometry:

plt.plot(lon, lat, color='blue', linewidth=2, marker='o', transform=ccrs.Geodetic())

If you want to add a straight line in planar geometry:

plt.plot(lon, lat, color='gray', linestyle='--', transform=ccrs.PlateCarree())

Most matplotlib plotting functions will work with cartopy projections: lines (plot), heatmaps and images (plot or imshow), scatter plots (scatter), vector plots (quiver). Let's plot our 2D atmospheric data with Cartopy projections. Read the data again:

import xarray as xr
data = xr.open_dataset('tasReduced.nc')
temp = data.tas.sel(time="2014-12-16") - 273.15   # extract last timestep, convert to Celsius
temp.shape      # (1, 64, 128)
temp.coords    # the coordinates are 1D, so plotting is easy

The data is defined on a 2D Cartesian projection. First, let's plot data in the same projection:

import cartopy.crs as ccrs
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(14,12))
ax = fig.add_subplot(111, projection=ccrs.PlateCarree())
ax.coastlines()
ax.gridlines()
temp.plot(ax=ax, cbar_kwargs={'shrink': 0.4})   # since we are using PlateCarree(), Cartopy assumes
                                                # that the data is also in PlateCarree() coordinates, which is true

Now let's switch the projection. Then we have to tell Cartopy our data's coordinate system explicitly with transform:

fig = plt.figure(figsize=(14,12))
ax = fig.add_subplot(111, projection=ccrs.InterruptedGoodeHomolosine())   # use this projection
ax.coastlines()
ax.gridlines()
temp.plot(ax=ax, transform=ccrs.PlateCarree(), cbar_kwargs={'shrink': 0.4})
            # `transform` tells Cartopy the coordinate system of our data

Let's switch the projection and zoom in on Vancouver Island:

ax = fig.add_subplot(111, projection=ccrs.Mollweide(-125))
ax.coastlines()
ax.gridlines()
temp.plot(ax=ax, transform=ccrs.PlateCarree(), cbar_kwargs={'shrink': 0.4})
ax.set_extent([-129, -122, 46, 53])

We can see that our data is really low resolution.

Working with ocean data

I took another ECCC historical model dataset (containing 3D ocean temperature) published on the CMIP6 Data-Archive and reduced its size picking only a subset of timesteps:

import xarray as xr
data = xr.open_dataset('/Users/razoumov/tmp/xarray/ocean/thetao_Omon_CanESM5_historical_r1i1p2f1_gn_201101-201412.nc')
data.sel(time=slice('2014-10-16', '2014-12-16')).to_netcdf("thetaoReduced.nc")     # last 3 steps

Let's download the file:

wget http://bit.ly/oceanfile -O thetaoReduced.nc

Estimating the file size 360x291x45 x 8 bytes x 3 steps / 1024^2 should result in 108MB, however, it is only 25MB due to NetCDF compression.

First, load it into ParaView:

  • use Vertical Scale = -1 and Vertical Bias = 5e4
  • pass through Threshold max = 100
  • Rescale to All Timesteps

Now, let's load this data and plot it in Matplotlib:

import xarray as xr
data = xr.open_dataset('thetaoReduced.nc')
data
data.thetao.min(), data.thetao.max()   # the data is in Celsius
data.thetao.shape
temp = data.thetao.isel(time=-1, lev=0)   # extract last timestep, elevation level 0
latIndexNearEquator = int(temp.shape[0]/2)
temp[latIndexNearEquator].values      # see how land is encoded with `nan`s
# temp[latIndexNearEquator] = 35
temp = data.isel(time=-1).thetao[0]    # extract last timestep, elevation level 0
temp.plot(size=8, cmap="viridis", vmin=-10, vmax=35)
temp.coords    # now coordinates are two-dimensional

In this plot we are using the 2D cell indices in x and y. If we want to plot in a non-Cartesian projection, we need to use data.coords. However, this dataset's coordinate system is unusual: it is a tripolar grid. Ideally, something like these lines should work -- but it does not:

# temp.plot(x="longitude", y = "latitude", size=8, cmap="viridis", vmin=-10, vmax=35)
# temp.plot.pcolormesh("longitude", "latitude")

So, this is an open question: how do you plot this dataset in an arbitrary projection using Cartopy?

My clumsy, very approximate solution:

temp.shape     # 291x360
import numpy as np
tnew = xr.DataArray(
    temp,
    dims=("lat","lon"),
    coords={"lat": np.linspace(-90,89.74176788,291), "lon": 73.5+np.linspace(0.01,359.99,360)}
)
fig = plt.figure(figsize=(14,12))
ax = fig.add_subplot(111, projection=ccrs.PlateCarree())   # use this projection
ax.coastlines()
ax.gridlines()
tnew.plot(ax=ax, cmap="viridis", vmin=-10, vmax=35, transform=ccrs.PlateCarree(), cbar_kwargs={'shrink': 0.4})
            # `transform` tells Cartopy the coordinate system of our data

Running Python scripts from the command line

In this lesson we'll work with bash command line, instead of the Jupyter notebook. We want to write a python script 'read.py' that takes a set of gapminder_gdp_*.csv files (one/few/many) as an argument and prints out various statistic (min, max, mean) for each year for all countries in that file:

$ ./read.py --min data-python/gapminder_gdp_{americas,europe}.csv   # minimum for each year
$ ./read.py --max data-python/gapminder_gdp_europe.csv              # maximum for each year
$ ./read.py --mean data-python/gapminder_gdp_europe.csv data-python/gapminder_gdp_asia.csv

It would be best to open two shells for the following programming, and keep nano always open in one shell.

Put the following into a file called read.py:

#!/usr/bin/env python
import sys
print('argument is', sys.argv)

and then run it from bash:

$ chmod u+x read.py
$ ./read.py     # it'll produce: argument is ['read.py'] (the name of the script is always there)
$ ./read.py one two three     # it'll produce: argument is ['read.py', 'one', 'two', 'three']

Let's modify our script:

import sys
print(sys.argv[1:])

$ python read.py one two three     # it'll produce ['one', 'two', 'three']

Let's modify our script:

import sys
for f in sys.argv[1:]:
    print(f)

$ python read.py one two three     # it'll produce one two three (one per line)
$ python read.py data-python/gapminder_gdp_*
$ python read.py data-python/gapminder_gdp_americas.csv data-python/gapminder_gdp_europe.csv
$ python read.py data-python/gapminder_gdp_{americas,europe}.csv     # same as last line

Let's actually read the data:

import sys
import pandas as pd
for f in sys.argv[1:]:
    print('\n', f[26:-4].capitalize())
    data = pd.read_csv(f, index_col='country')
    print(data.shape, '\n')

$ python read.py data-python/gapminder_gdp_{americas,europe}.csv
$ wc -l !$      # the output should be consistent

Let's modify our script changing print(data.shape) -> print(data.mean()) to compute average per year for each file:

$ python read.py data-python/gapminder_gdp_{americas,europe}.csv

Let's add an action flag and calculate statistics based on the flag:

import sys
import pandas as pd
action = sys.argv[1]
for f in sys.argv[2:]:
    print('\n', f[26:-4].capitalize())
    data = pd.read_csv(f, index_col='country')
    if 'continent' in data.columns.tolist():   # if 'continent' column exists
        data = data.drop('continent',1)        #     delete it (1 stands for column, 0 for row)
    if action == '--min':
        values = data.min().tolist()
    elif action == '--mean':
        values = data.mean().tolist()
    elif action == '--max':
        values = data.max().tolist()
    print(values,'\n')

$ python read.py --min data-python/gapminder_gdp_{americas,europe}.csv
$ python read.py --max data-python/gapminder_gdp_{americas,europe}.csv
$ python read.py --mean data-python/gapminder_gdp_{americas,europe}.csv
$ python read.py --mean data-python/gapminder_gdp_*.csv   # should print data for all five continents

Let's add assertion for action (syntax is: assert n > 0.0, 'should be positive') right after the definition of action:

assert action in ['--min', '--mean', '--max'], 'action must be one of: --min --mean --max'

and try passing some other action.

Now let's package processing of a file (reading + computing + printing) as a function:

import sys
import pandas as pd
action = sys.argv[1]
assert action in ['--min', '--mean', '--max'], 'action must be one of: --min --mean --max'
filenames = sys.argv[2:]
def process(filename, action):
    print('\n', filename[26:-4].capitalize())
    data = pd.read_csv(filename, index_col='country')
    if 'continent' in data.columns.tolist():   # if 'continent' column exists
        data = data.drop('continent',1)        #     delete it (1 stands for column, 0 for row)
    if action == '--min':
        values = data.min().tolist()
    elif action == '--mean':
        values = data.mean().tolist()
    elif action == '--max':
        values = data.max().tolist()
    print(values,'\n')
for f in filenames:
    process(f, action)

Adding standard input support to Python scripts

Python scripts can process standard input. Consider the following script:

#!/usr/bin/env python
import sys
for line in sys.stdin:
    print(line, end='')

In the terminal make it executable (chmod u+x scriptName.py), and then run it:

./scriptName.py                          # repeat each line you type until Ctrl-C
echo one two three | ./scriptName.py     # print back the line
cat file.extension | ./scriptName.py     # process this file (filename=sys.stdin) from standard input
tail -1 scriptName.py | ./scriptName.py      # print its own last line

Let's add support for Unix standard input. Delete 'print('\n', f[26:-4].capitalize())' and change the last two lines to:

if len(filenames) == 0:
    process(sys.stdin,action)       # process standard input
else:
    for f in filenames:             # same as before
        print('\n', f[26:-4].capitalize())
        process(f,action)

$ python read.py --mean data-python/gapminder_gdp_europe.csv
$ python read.py --mean < data-python/gapminder_gdp_europe.csv    # anyone knows why this could be useful?

Here is why: you can do preprocessing in bash before passing the data to your Python script, e.g.

$ head -5 data-python/gapminder_gdp_europe.csv | python read.py --mean    # process only first five countries
cp data-python/gapminder_gdp_asia.csv a1
cat data-python/gapminder_gdp_europe.csv | sed '1d' >> a1   # add all European data without the header
cat a1 | python read.py --mean          # merge Asian and European data and calculate joint statistics

Here is our full script:

import sys
import pandas as pd
action = sys.argv[1]
assert action in ['--min', '--mean', '--max'], 'action must be one of: --min --mean --max'
filenames = sys.argv[2:]
def process(filename, action):
    data = pd.read_csv(filename, index_col='country')
    if 'continent' in data.columns.tolist():   # if 'continent' column exists
        data = data.drop('continent',1)        #     delete it (1 stands for column, 0 for row)
    if action == '--min':
        values = data.min().tolist()
    elif action == '--mean':
        values = data.mean().tolist()
    elif action == '--max':
        values = data.max().tolist()
    print(values,'\n')
if len(filenames) == 0:
    process(sys.stdin,action)       # process standard input
else:
    for f in filenames:             # same as before
        print('\n', f[26:-4].capitalize())
        process(f,action)

Basics of object-oriented programming in Python

Object-oriented programming is a way of programming in which you bundle related variables and functions into objects, and then manipulate and use these objects as a whole. We already saw many examples of objects on Python, e.g. lists, dictionaries, numpy arrays, that have both variables and methods inside them. In this section we will learn how to create our own objects.

You can think of:

  • variables as properties / attributes of an object
  • functions as some operations / methods you can perform on this object

Let's define out first class:

class Planet:
    # internally we store all numbers in cgs units
    hostObject = "Sun"     # class attribute (the same value for every class instance)
    def __init__(self, radius, mass):   # sets the initial state of a newly created object
        self.radius = radius*1e5   # instance attribute, convert km -> cm
        self.mass = mass*1.e3      # instance attribute, convert kg->g

Let's define some instances of this class:

mercury = Planet(radius=2439.7, mass=3.285e23) # enter km and kg
venus = Planet(6051.8, 4.867e24)               # enter km and kg
venus.radius, venus.mass, venus.hostObject

Instances are guaranteed to have the attributes that we expect.

Question: How can we define an instance without passing the values? E.g., I would like to say earth=Planet() and then pass the attribute values separately like this:

earth = Planet()
earth.radius = 6371         # these are dynamic variables that we can redefine
earth.mass = 5.972e24
Planet().radius      # prints 'nan'

Let's add inside our class an instance method (with proper indentation):

    def density(self):   # it acts on the class instance
        return self.mass/(4./3.*math.pi*self.radius**3) # [g/cm^3]

Redefine the class, and now:

earth = Planet()
earth.radius = 6371*1e5      # here we need to convert manually
earth.mass = 5.972e24*1e3
import math
earth.density()    # 5.51 g/cm^3

Let's add another method (remember the indentation!):

    def g(self):   # free fall acceleration
        return 6.67259e-8*self.mass/self.radius**2    # G in [cm^3/g/s^2]

and now

earth = Planet(6371,5.972e24)
mars = Planet(3389.5,6.39e23)
earth.g()              # 981.7 cm/s^2
mars.g() / earth.g()   # 0.378

Let's add another method (remember the indentation!):

    def describe(self):
        print('density =', self.density(), 'g/cm^3')
        print('free fall =', self.g(), 'cm/s^2')

Redefine the class, and now:

jupyter = Planet(radius=69911, mass=1.898e27)
jupyter.describe()       # should print 1.32 g/cm^3 and 2591 cm/s^2
print(jupyter)           # says it is an object at this memory location (not very descriptive)

Let's add our last method (remember the indentation!):

    def __str__(self):    # special method to redefine the output of print(self)
        return f"My radius is {self.radius/1e5}km and my mass is {self.mass/1e3}kg"

Redefine the class, and now:

jupyter = Planet(radius=69911, mass=1.898e27)
print(jupyter)        # prints the full sentence

Important: As with any complex object in Python, assigning an instance to a new variable will simply create a pointer, i.e. if you modify one in place, you'll see the change through the other one too:

new = jupyter
jupyter.mass = -1
new.mass     # also -1

If you want a separate copy:

import copy
new = copy.deepcopy(jupyter)
jupyter.mass = -2
new.mass     # still -1

Inherit from parent classes

Let's create a child class Moon that would inherit the attributes and methods of Planet class:

class Moon(Planet):    # it inherits all the attributes and methods of the parent process
    pass

phobos = Moon(radius=22.2, mass=1.08e16)
deimos = Moon(radius=12.6, mass=2.0e15)
phobos.g() / earth.g()        # 0.0001489
isinstance(phobos, Moon)         # True
isinstance(phobos, Planet)       # True - all objects of a child class are instances of the parent class
isinstance(jupyter, Planet)      # True
isinstance(jupyter, Moon)        # False
issubclass(Moon,Planet)      # True

Child classes can have their own attributes and methods that are distinct from (i.e. override) the parent class:

class Moon(Planet):
    hostObject = 'Mars'
    def g(self):
        return 'too small to compute accurately'
    
phobos = Moon(radius=22.2, mass=1.08e16)
deimos = Moon(radius=12.6, mass=2.0e15)
mars = Planet(3389.5,6.39e23)
phobos.hostObject, mars.hostObject     # ('Mars', 'Sun')
phobos.g(), mars.g()                   # ('too small to compute accurately', 371.1282569773226)

One thing to keep in mind about class inheritance is that changes to the parent class automatically propagate to child classes (when you follow the sequence of definitions), unless overridden in the child class:

class Parent:
	...
    def __str__(self):
        return "Changed in the parent class"
	...

class Moon(Planet):
    hostObject = 'Mars'
    def g(self):
        return 'too small to compute accurately'

deimos = Moon(radius=12.6, mass=2.0e15)
print(deimos)            # prints "Changed in the parent class"

You can access the parent class namespace from inside a method of a child class by using super():

class Moon(Planet):
    hostObject = 'Mars'
    def parentHost(self):
        return super().hostObject       # will return hostObject of the parent class

deimos = Moon(radius=12.6, mass=2.0e15)
deimos.hostObject, deimos.parentHost()     # ('Mars', 'Sun')

Generators

We already saw that in Python you can loop over a collection using for:

for i in 'weather':
    print(i)
for j in [5,6,7]:
    print(j)

Behind the scenes Python creates an iterator out of a collection. This iterator has a __next__() method, i.e. it does something like:

a = iter('weather')
a.__next__()    # 'w'
a.__next__()    # 'e'
a.__next__()    # 'a'

You can build your own iterator as if you were defining a function - this is called a generator in Python:

def square(x):   # `x` is an input string in this generator
    for letter in x:
        yield int(letter)**2        # yields a sequence of numbers that you can cycle through

[i for i in square('12345')]     # [1, 4, 9, 16, 25]

a = square('12345')
[a.__next__() for i in range(3)]      # [1, 4, 9, 16, 25]

Programming Style and Wrap-Up

  • comment your code as much as possible
  • use meaningful variable names
  • very good idea to break complex programs into blocks using functions
  • change one thing at a time, then test
  • use revision control
  • use docstrings to provide online help
def average(values):
    "Return average of values, or None if no values are supplied."
    if len(values) > 0:
        return(sum(values)/len(values))

print(average([1,2,3,4]))
print(average([]))
help(average)

def moreComplexFunction(values):
    """This string spans
       multiple lines.

    Blank lines are allowed."""

help(moreComplexFunction)
  • very good idea to add assertions to your code to check things
assert n > 0., 'Data should only contain positive values'

is the same as

import sys
if n <= 0.:
    print('Data should only contain positive values')
    sys.exit(1)

Other advanced Python topics

  • list.sort() and list.index(value); heterogeneous lists
  • to/from matplotlib, to/from numpy