You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
现有如下的一个图,节点是城市,边是城市之间的距离,需要找到从一个城市到另一个城市的最短路径。
起点:San Francisco (SF),终点:Phoenix (PX). 途中可能经过的城市:Monterey (MT), San Jose (SJ), Santa Barbara (SB), Los Angeles (LA), San Diego (SD), Fresno (FR), Bakersfield (BK), Las Vegas (LV).
var_=require('lodash');classDijkstra{solve(graph,start,end){// track costs of each nodeconstcosts=graph[start];// set end to infinite on 1st passcosts[end]=Infinity;// remember path from// which each node was visitedconstpaths={};// add path for the start nodes neighbors_.forEach(graph[start],(dist,city)=>{// e.g. city SJ was visited from city SFpaths[city]=start;});// track nodes that have already been visited nodesconstvisitedNodes=[];// get current nodes cheapest neighborletcurrentCheapestNode=this.getNextLowestCostUnvisitedNode(costs,visitedNodes);// while node existswhile(currentCheapestNode){// get cost of reaching current cheapest nodeletcostToReachCurrentNode=costs[currentCheapestNode];// access neighbors of current cheapest nodeletneighbors=graph[currentCheapestNode];// loop over neighbors_.forEach(neighbors,(dist,neighbor)=>{// generate new cost to reach each neighborletnewCost=costToReachCurrentNode+dist;// if not already added// or if it is lowest cost amongst the neighborsif(!costs[neighbor]||costs[neighbor]>newCost){// add cost to list of costscosts[neighbor]=newCost;// add to pathspaths[neighbor]=currentCheapestNode;}});// mark as visitedvisitedNodes.push(currentCheapestNode);// get cheapest node for next nodecurrentCheapestNode=this.getNextLowestCostUnvisitedNode(costs,visitedNodes);}// generate responseletfinalPath=[];// recursively go to the startletpreviousNode=paths[end];while(previousNode){finalPath.unshift(previousNode);previousNode=paths[previousNode];}// add end node at the endfinalPath.push(end);// return responsereturn{distance: costs[end],path: finalPath};}getNextLowestCostUnvisitedNode(costs,visitedNodes){//extract the costs of all non visited nodescosts=_.omit(costs,visitedNodes);// return the node with minimum costreturn_.minBy(_.keys(costs),(node)=>{returncosts[node];});}}
Using Dijkstra to determine the shortest path
现有如下的一个图,节点是城市,边是城市之间的距离,需要找到从一个城市到另一个城市的最短路径。
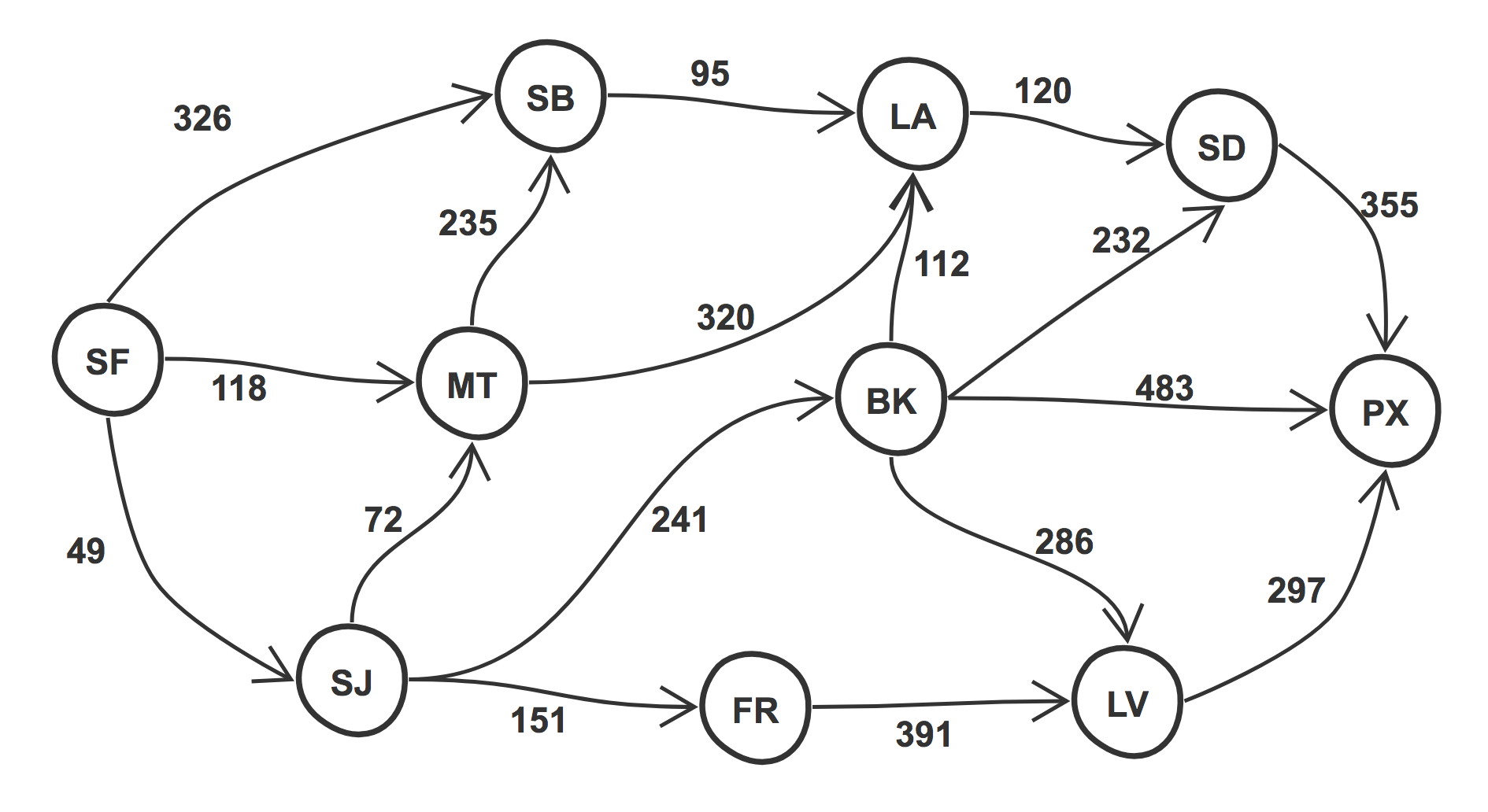
起点:San Francisco (SF),终点:Phoenix (PX). 途中可能经过的城市:Monterey (MT), San Jose (SJ), Santa Barbara (SB), Los Angeles (LA), San Diego (SD), Fresno (FR), Bakersfield (BK), Las Vegas (LV).
首先要初始化所有的变量,一个用来记录经过每一个节点的花费,一个用来记录走过的路径,另一个记录已经访问过的节点以避免重复计算。
这里的
solve()方法初始化了costs变量,并将开始节点的cost值赋值给它,然后将结束节点的cost值设置为Infinity. 这就意味着在开始阶段,costs集合包含了所有的节点和边同样的数据。从上面的代码中可以看出,
currentCheapestNode在首次迭代的时候值为SJ,基于costs和visitedNodes数组。一旦找到了第一个节点,那么就可以访问到它的邻居节点,并且更新
costs的值(只有在它的costs小于当前节点的cost).如果cost更小,这就说明了我们想通过这个节点到达结束节点是合乎逻辑的,所以也同样更新到他邻居的路径。然后就开始递归的进行这个过程,在递归结束时,我们就能得到更新过后的所有节点的costs,并且得到到结束节点的最后cost.Reference: 《Hands-on Data Structures and Algorithm with JavaScript》
The text was updated successfully, but these errors were encountered: