Repositorio asociado a la tesis "Optimización del cociente de la traza para Máquinas de Aprendizaje"
En esta tesis se aborda el problema de optimización planteado por el Análisis Discriminante Lineal de Fisher (ADLF); el cuál, puede ser utilizado para resolver para problemas de clasificación. El ADLF busca maximizar un cociente de la forma:
Sobre el conjunto de matrices ortogonales V con p columnas y A, B matrices positivas definidas. Este problema era considerado computacionalmente difícil de resolver, por lo que era reemplazado por otras versiones simplificadas. Se busca demostrar que el ADLF, resuelto a través del método de Newton y del algoritmo de Lanczos, brinda una precisión comparable con otros algoritmos de clasificación lineales y con un tiempo de cómputo similar.
Se comienza el primer capítulo introduciendo al ADLF dentro del contexto de aprendizaje de máquina; en particular, como un problema de clasificación lineal. Después, se busca la solución cuando V es un vector. En seguida se proporciona la generalización a p dimensiones. Para finalizar el capítulo, se demuestra que el ADLF es equivalente a un problema escalar, por lo que se puede expresar en términos de una
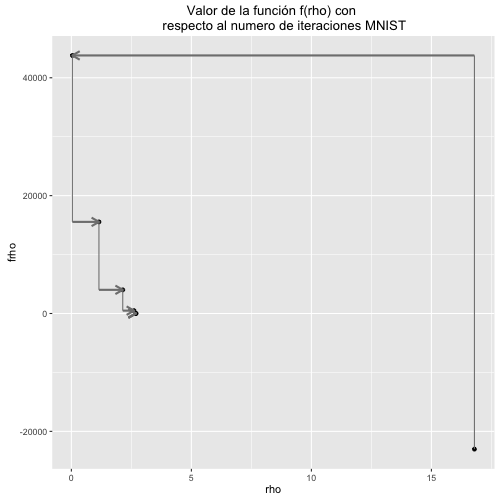
El segundo capítulo aborda el método para resolver el ADLF: Newton-Lanczos. Al inicio, se da una breve presentación de la teoría que sustenta a los métodos de Lanczos, su costo computacional y las ventajas que tienen sobre los métodos tradicionales. En seguida, se enuncia el algoritmo para alcanzar la solución óptima: el algoritmo de Newton-Lanczos. Al tener como base el método de Newton, se requiere del cómputo de la derivada de
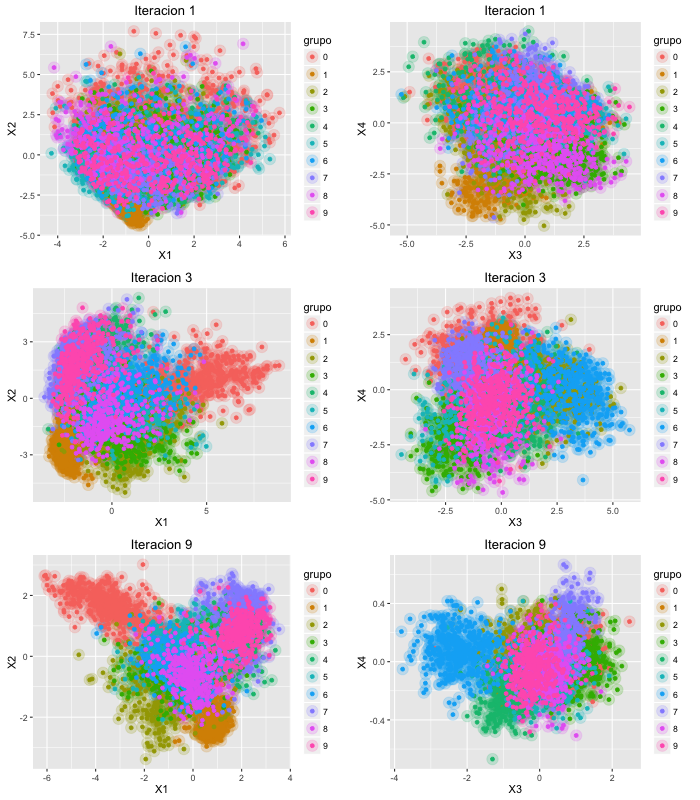
En el tercer capítulo se presentan los experimentos numéricos sobre las bases JAFFE y MNIST.
Se da una breve introducción de su preprocesamiento, para continuar con un ejemplo donde se proyecta a una dimensión de tamaño 20. Al final, se compara la precisión del ADLF vía Newton-Lacnzos contra el Análisis Discriminante Lineal (ADL) y la Regresión Logística Múltiple (RLM) para diferentes p. Al final, se realiza una comparación del tiempo de cómputo.
Para este proyecto se utilizó una plantilla de proyectos de anális, llamada "Project Template". A continuación se muestra el contenido de las carpetas:
cache/ Datos procesados guardados en disco para rápido acceso config/ Contiene el archivo global.dcf para modificar el comportamiento del proyecto data/ Contiene los archivos originales graphs/ Contiene las imágenes creadas en el proyecto lib/ Contiene las funciones que se leen al cargar el proyecto munge/ Contiene el preprocesamiento de los datos packrat/ Contiene las librerias usadas (es el manejador de versiones que se utiliza) profiling/ Código para ver el tiempo que toma en correr los programas reports/ Contiene reportes con los resultados src/ Contiene los códigos que se utilizaron en el proyecto
Para cargar la paquetería y los archivos que se encuentran en cache, se utiliza la siguiente linea:
library(ProjectTemplate) reload.project()
Esta carga en nuestro environment los datasets procesados y las librerias a usar.
Si se requiere ver el preprocesamiento de los datos, se sugiere ir a la carpeta de config y modificar el archivo global.dcf activando la función de munging. (el código está) en la carpeta de "munge".
Si se desean ver los códigos que generan las gráficas, estos se encuentran en la carpeta src/
Si se desean ver las funciones programadas, están en la carpeta de lib/
Si solo se desea correr todo el código para generar los resultados presentados en la tesis, ir a la carpeta de src/ y correr en el orden especificado.
Las conclusiones más relevantes de esta tesis son las siguientes:
- Se implementó computacionalmente una técnica de optimización que anteriormente resultaba difícil de resolver.
- Una de las principales ventajas de esta metodología es que no requiere ningún supuesto sobre la distribución de los datos.
- Se evaluó el desempeño de esta metodología con respecto a técnicas conocidas y los resultados fueron satisfactorios.
- Se realizaron dos pruebas diferentes y se obtuvo que en algunos casos el ADLF vía Newton-Lanczos tuvo una precisión mayor con respecto a los otros dos métodos. \end{itemize}
Una de las complicaciones del algoritmo de Lanczos es la reortogonalización de la base. En este estudio se utilizó el método de reortogonalización completa; sin embargo, existen modificaciones al algoritmo que pueden ser exploradas con el objetivo de lograr mayor eficiencia en términos computacionales. Por ejemplo, J.W. Demmel (1997) \cite{demmel1997applied} propone algunas alternativas que pueden ser utilizadas para mejorar el proceso de reortogonalización de la base en el algoritmo de Lanczos.