-
Notifications
You must be signed in to change notification settings - Fork 61
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Analysing time-series data #78
Comments
|
Hello Wolfgang,
Glad you've overall had a good experience with ripser.py so far!
Wow, this is quite an interesting case. Because in a metric space d(x, y)
= 0 if and only if x=y, we never expect there to be zeros in the distance
matrix. But I see why you would want to use them with trajectories to
bully the filtration into adding the edges between subsequent points in
time first. Unfortunately, zeros in a sparse matrix are interpreted to be
infinity (edges that are never added). Because I can't think of a clean
way to change the API to allow actual zeros in the sparse matrix (and
because it may not be such a general thing to do), what I would recommend
as a hack for the moment is to make the edges between t and t+1 a very
small number, which is orders of magnitude below any other edges you have
(so maybe something like 1e-14). That should get you basically the results
you're seeing with dense matrices.
I hope that's a reasonable answer for now. I'm curious to see what you end
up doing with time series, as I also do a lot of work on trajectories.
Best,
Chris
…On Mon, Jul 8, 2019 at 6:53 AM Wolfgang Merkt ***@***.***> wrote:
Hi guys,
Thank you very much for your hard work in developing and maintaining this
excellent tool - it really is a breeze to work with!
We are currently working on problems involving time-series data
(trajectories). In order to achieve this, we post-process the distance
matrix D to set the distance between subsequent points (t and t+1) to 0.
This works just fine with dense filtration and we obtain the results that
we expect. With sparse/approximate filtration, however, this breaks (maybe
because the 0 to be interpreted as a sparse entry?). As our datasets
usually are larger than the synthetic ones we used to test, ripser.py often
runs out of memory and we'd like to leverage the approximate filtration. Do
you have any advice or perhaps best practices for dealing with time-series
data and approximate filtration?
Thank you very much,
Wolfgang
—
You are receiving this because you are subscribed to this thread.
Reply to this email directly, view it on GitHub
<#78?email_source=notifications&email_token=AAJWDZUYRHB4N23C7NDQIG3P6MMBHA5CNFSM4H62NOF2YY3PNVWWK3TUL52HS4DFUVEXG43VMWVGG33NNVSW45C7NFSM4G52G5XQ>,
or mute the thread
<https://github.com/notifications/unsubscribe-auth/AAJWDZRKGJPA3XEW7HJ6HN3P6MMBHANCNFSM4H62NOFQ>
.
|
|
Hi Chris, Thank you very much - best, |
|
Hi Wolfgang,
The results should be very close if you make them a number close to zero,
so it's a bit alarming that they're not. Hopefully there's not another
issue with sparse matrices lurking there!
So I have seen the trick you're using before, but I never personally use it
when I apply TDA to trajectories. Instead, I represent local time
information via sliding window embeddings. I have some notebooks on this
here:
https://github.com/ctralie/TDALabs
Best,
Chris
…On Mon, Jul 8, 2019 at 9:21 AM Wolfgang Merkt ***@***.***> wrote:
Hi Chris,
Thank you very much for your quick response - I will try it (we have
previously used 1e-6 instead of zero, and it only worked so-so). Do you
mind sharing what approaches you use to represent trajectories when passing
them to ripser.py?
Thank you very much - best,
Wolfgang
—
You are receiving this because you commented.
Reply to this email directly, view it on GitHub
<#78?email_source=notifications&email_token=AAJWDZXS3LYUTPMUCDCZ2R3P6M5O3A5CNFSM4H62NOF2YY3PNVWWK3TUL52HS4DFVREXG43VMVBW63LNMVXHJKTDN5WW2ZLOORPWSZGODZNB6BI#issuecomment-509222661>,
or mute the thread
<https://github.com/notifications/unsubscribe-auth/AAJWDZWWUB6ZZGG6MRFZYUDP6M5O3ANCNFSM4H62NOFQ>
.
|
|
@wxmerkt a bit late to the party here but, in my experience, things work out as I think you would like them to in When making |
|
Thank you Umberto, that is very helpful!
…On Fri, Aug 21, 2020 at 11:55 AM Umberto Lupo ***@***.***> wrote:
@wxmerkt <https://github.com/wxmerkt> a bit late to the party here but,
in my experience, things work out as I think you would like them to in
ripser.py if you explicitly store zeros in your sparse matrices (this can
be done in a number of scipy sparse formats). I can show you an example
if you like (perhaps this got solved in the meantime?).
When making pyflagser <https://github.com/giotto-ai/pyflagser> (docs
<https://docs-pyflagser.giotto.ai/>), we had to face some similar
conundrums concerning the expected format of sparse matrices. In the end,
we settled on a design choice which is explained in the function
flagser_weighted
<https://docs-pyflagser.giotto.ai/generated/pyflagser.flagser_weighted.html#pyflagser.flagser_weighted>
-- analogous to ripser (it computes the *same* persistence diagrams when
directed=False is passed!). In brief, you can pass sparse adjacency
matrices with *explicitly stored* zeros and they are treated as zero
filtration parameters, not as absent edges. The absent edges, as @ctralie
<https://github.com/ctralie> pointed out is the case also in ripser.py,
are the non-stored entries in the sparse matrix (the "sparse zeros", if you
will).
—
You are receiving this because you were mentioned.
Reply to this email directly, view it on GitHub
<#78 (comment)>,
or unsubscribe
<https://github.com/notifications/unsubscribe-auth/AAJWDZXESUKKXSTDXPG4NKLSB2KILANCNFSM4H62NOFQ>
.
|
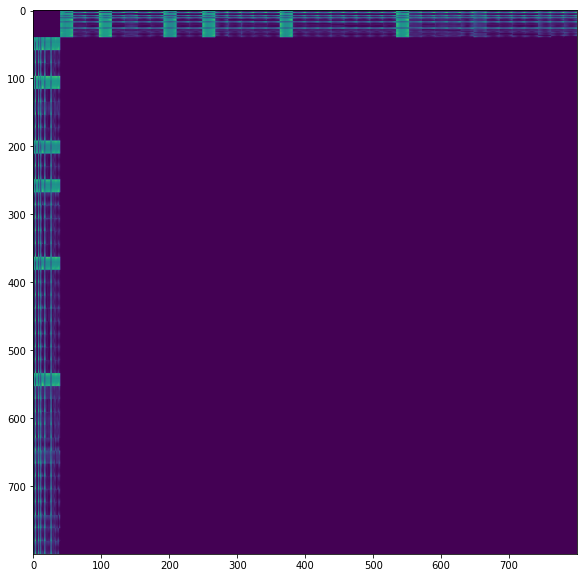
Hi guys,
Thank you very much for your hard work in developing and maintaining this excellent tool - it really is a breeze to work with!
We are currently working on problems involving time-series data (trajectories). In order to achieve this, we post-process the distance matrix
Dto set the distance between subsequent points (tandt+1) to0. This works just fine with dense filtration and we obtain the results that we expect. With sparse/approximate filtration, however, this breaks (maybe because the0to be interpreted as a sparse entry?). As our datasets usually are larger than the synthetic ones we used to test, ripser.py often runs out of memory and we'd like to leverage the approximate filtration. Do you have any advice or perhaps best practices for dealing with time-series data and approximate filtration?Thank you very much,
Wolfgang
The text was updated successfully, but these errors were encountered: