Statistics.md

概率论只不过是把常识用数学公式表达了出来。
——拉普拉斯

概率论（Probability theory）是研究随机性或不确定性等现象的数学。更精确地说，概率论是用来模拟实验在同一环境下会产生不同结果的情况。典型的随机实验有掷骰子、扔硬币、抽扑克牌以及轮盘游戏等。

人们对概率总是有一点触摸不清的感觉，而事实上也有很多看似奇异的结果：

• 生日悖论：在一个足球场上有23个人（2×11个运动员和1个裁判员），不可思议的是，在这23人当中至少有两个人的生日是在同一天的概率要大于50％。
• 轮盘游戏：在游戏中玩家可能认为，在连续出现多次红色后，出现黑色的概率会越来越大。这种判断是错误的，即出现黑色的概率每次是相等的，因为球本身并没有“记忆”， 它不会意识到以前都发生了什么，其概率始终是 18/37。

事件

在一次随机试验中可能发生的不能再细分的结果被称为基本事件，或者称为单位事件，用 E 表示。在随机试验中可能发生的所有单位事件的集合称为事件空间，用 S 来表示。例如在一次掷骰子的随机试验中，如果用获得的点数来表示单位事件，那么一共可能出现 6 个单位事件，则事件空间可以表示为 S={1,2,3,4,5,6}。

上面的事件空间是由可数有限单位事件组成，事实上还存在着由可数无限以及不可数单位事件组成的事件空间，比如在一次获得正面朝上就停止的随机掷硬币试验中，其事件空间由可数无限单位事件组成，表示为：S={ 正，反正，反反正，反反反正，反反反反正，···}，注意到在这个例子中"反反反正"是单位事件。

随机事件 是事件空间 S 的子集，它由事件空间 S 中的单位元素构成，用大写字母 A,B,C 表示。例如在掷两个骰子的随机试验中，设随机事件 A = “获得的点数和大于10”，则 A 可以由下面 3 个单位事件组成：A={(5,6),(6,5),(6,6)}。 如果在随机试验中事件空间中的所有可能的单位事件都发生，这个事件被称为必然事件，表示为 S ⊂ S ；相应的如果事件空间里不包含任何一个单位事件，则称为不可能事件，表示为 ∅ ⊂ S 。

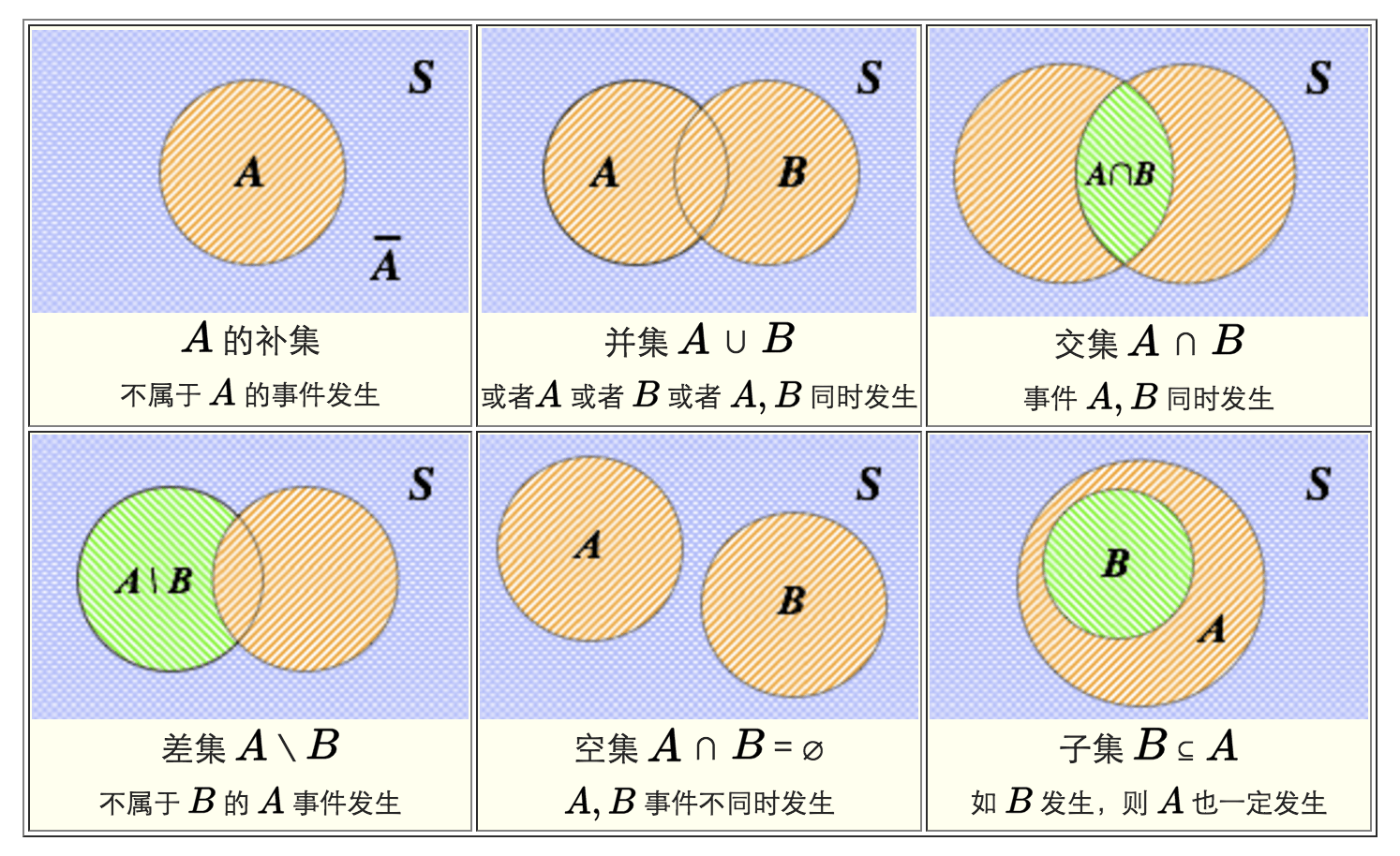
因为事件在一定程度上是以集合的含义定义的，因此可以把集合计算方法直接应用于事件的计算，也就是说，在计算过程中，可以把事件当作集合来对待。

在轮盘游戏中假设 A 代表事件“球落在红色区域”，B 代表事件"球落在黑色区域"，因为事件A 和 B 没有共同的单位事件，因此可表示为 A ∩ B = ∅。

概率的定义

传统概率的定义是由法国数学家拉普拉斯 (Laplace) 提出的。如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验。在拉普拉斯试验中，事件 A 在事件空间 S 中的概率 P(A) 为：

P(A) = 构成事件 A 的元素的数目 / 构成事件空间 S 的所有元素的数目

传统概率在实践中被广泛应用于确定事件的概率值，其理论根据是：如果没有足够的论据来证明一个事件的概率大于另一个事件的概率，那么可以认为这两个事件的概率值相等。

统计概率

继传统概率论之后，英国逻辑学家约翰·维恩和奥地利数学家理查德提出建立在频率理论基础上的统计概率。他们认为，获得一个事件的概率值的唯一方法是通过对该事件进行 100 次，1000 次或者甚至 10000 次的前后相互独立的 n 次随机试验，针对每次试验均记录下绝对频率值h_n(A)和相对频率值f_n(A)，随着试验次数 n 的增加，会出现如下事实，即相对频率值会趋于稳定，它在一个特定的值上下浮动，也即是说存在着一个极限值 P(A)，相对频率值趋向于这个极限值。这个极限值被称为统计概率，表示为：

例如，若想知道在一次掷骰子的随机试验中获得 6 点的概率值可以对其进行 3000 次前后独立的扔掷试验，在每一次试验后记录下出现 6 点的次数，然后通过计算相对频率值可以得到趋向于某一个数的统计概率值。

贝叶斯定理

考虑这样一个问题：

现分别有 A，B 两个容器，在容器 A 里分别有 7 个红球和 3 个白球，在容器 B 里有 1 个红球和 9 个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器 A 的概率是多少?

这类典型的问题可以用贝叶斯定理来解决，更多内容参考 BayesTheorem

牛课题目

［随机事件概率关系］
［半小时内汽车通过概率］
［书的摆放方式］
［两个孩子一个是男孩，两个都是男孩的概率］
［连续抛硬币无穷次，稳定时分布］

更多阅读