Keywords: Queue, Stack, Binary Tree (search, insert, delete, remove, balance)
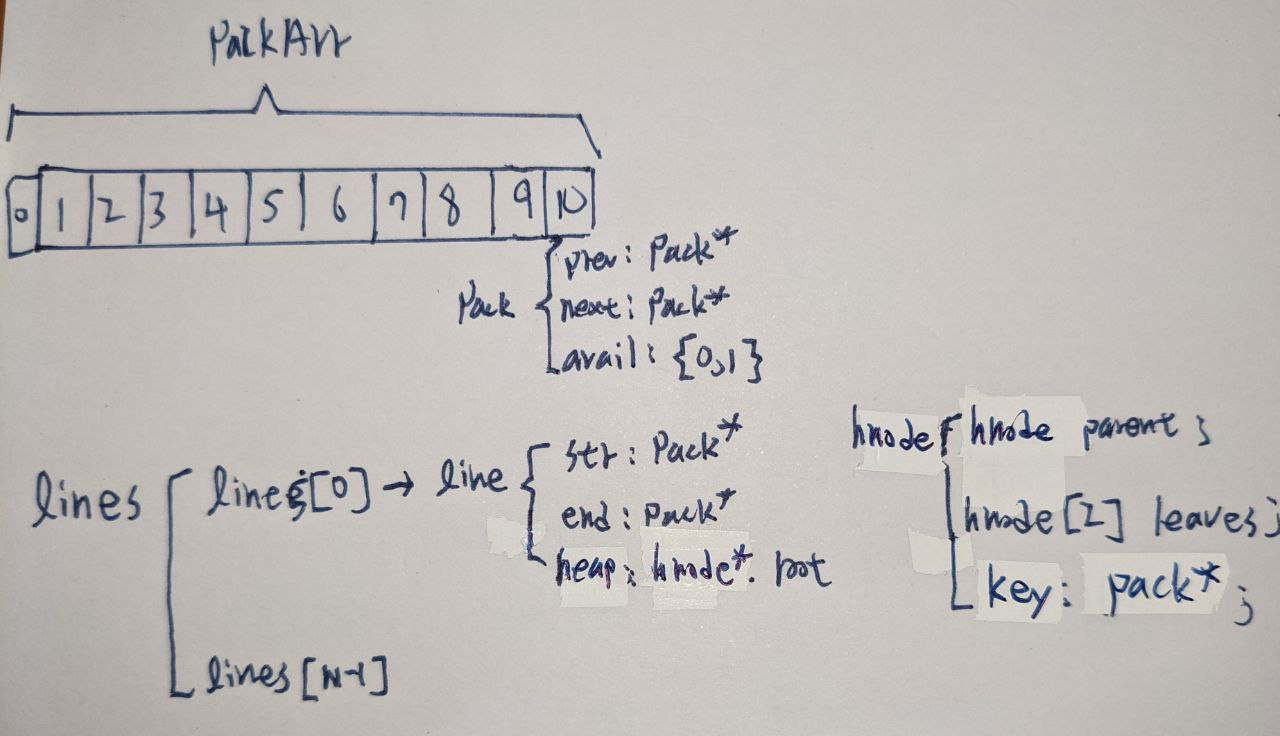
Lproduction linesNpackagesOOperations
-
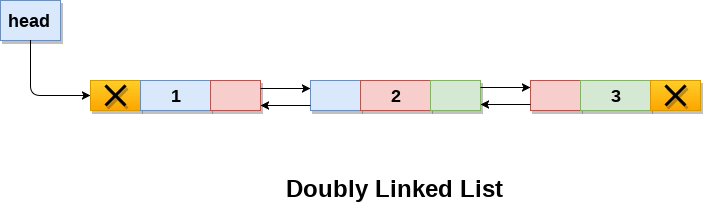
Production line
-
Peaking a production line
getFirst:O(1)getLast:O(1)getMax:O(1)
-
Operation
PopFirst:O(n)PopLast:O(n)PopMax:O(log n)
-
Merge Production line
- Deque
Ref:
Ref
- Balancing a binary search tree (GO)
- AVL Tree: Insertion (GreekforGeek)
- AVL Tree: Deletion (GreekforGeek)
- 資料結構與演算法:AVL Tree
| Operation | Time |
|---|---|
| Search | O(log n) |
| Insert | O(log n) |
| Delete | O(log n) |
- Advantage of using AVL Tree
- Guarantee: O(log n) for binary search
Ref:
- Merge 要求
log(n)
- 用 Heap: 快速找到 max, first, last
- Time complexity of merge: <O(n)
deallocate (node):
//do nothing if passed a non-existent node
if node is null
return
//now onto the recursion
deallocate(left node)
deallocate(right node)
free node
Ref: stackoverflow
Ref: web
#include <stdio.h>
// A normal function with an int parameter
// and void return type
void fun(int a)
{
printf("Value of a is %d\n", a);
}
int main()
{
void (*fun_ptr)(int) = fun; // & removed
fun_ptr(10); // * removed
return 0;
}Ref: GreekforGeek
int (*fun[3])(packData, int)= {PeekFirstPack, PeekLastPack, PeekMaxPack};-
Partial declaration
Ref:
- https://tmt514.gitbooks.io/2016-09/content/tree-ds/leftist-tree.html
- http://sunmoon-template.blogspot.com/2014/12/leftist-tree.html
- https://www.humblec.com/c-implementation-leftist-tree/
- Tutorial: Leftist Tree
- Stack, Queue and Heap. [GitBook]