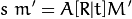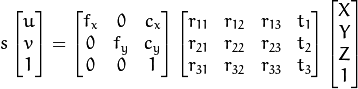Este projeto tem como objetivo estimar a posição de um objeto em 3D a partir de algoritmos de visão computacional. O programa recebe como entrada um vídeo em tempo real e tenta encontrar a posição do objeto em cada imagem. O objeto a ser rastreado precisa estar coberto por marcadores luminosos e o arranjo dos marcadores deve ser fixo relativo ao objeto e conhecido previamente. Idealmente, os marcadores devem ser mais claros que a iluminação ambiente para que se destaquem e sejam fáceis de encontrar. Durante o desenvolvimento foram testados como marcadores lâmpadas LED e imagens numa tela LCD de celular.
O processo realizado pelo programa pode ser separado em três partes principais: detecção de marcadores, associação de marcadores, e estimativa de posição. Porém antes disso também é necessário um estágio adicional de preparação para que o programa funcione corretamente: a calibração.
Toda câmera é diferente e por isso cada uma captura imagens de maneira distinta. Propriedades como a distância focal, resolução e coeficientes de distorção afetam de maneiras diferentes a aparência final das imagens de uma dada câmera. A este conjunto de propriedades dá se o nome de parâmetros intrínsecos da câmera. Para que o programa seja capaz de extrair informações úteis das imagens que recebe de entrada, é necessário que estes parâmetros intrínsecos sejam conhecidos anteriormente. Por isso a medição destes parâmetros através da calibração da câmera é um passo essencial para o funcionamento correto do programa.
Os algoritmos de visão computacional utilizados nesse projeto se baseiam em um modelo matemático chamado de câmera pinhole. Segundo este modelo, a projeção dos pontos 3D para o espaço 2D da imagem pode ser descrito da seguinte forma:
Mais detalhadamente, isto equivale ao seguinte sistema:
Isto é, a posição M' do ponto descrita em coordenadas homogêneas sofre uma transformação [R|t] de acordo com sua rotação e posição em 3D. Após este passo, o resultado é tomado em coordenadas homogêneas como a projeção do ponto em 2D. Finalmente, o ponto sofre uma transformação A adicional que leva à posição m' em pixels dentro da imagem. Neste caso, observa-se que a matriz A é construída a partir dos parâmetros intrínsecos da câmera (distância focal e resolução) e por isso é conhecida. Também são conhecidos M' e m' já que equivalem à posição dos marcadores e suas projeções na imagem, respectivamente. Já a matriz [R|t] não é conhecida já que depende da posição do objeto.
Além do modelo matemático descrito acima, câmeras reais também realizam distorções adicionais sobre a projeção dos pontos na imagem. Estas distorções são causadas pelo formato das lentes das câmeras e o alinhamento imperfeito das lentes em relação ao sensor fotográfico. A estas distorções dá se o nome de distorção radial e tangencial, respectivamente. Seguem abaixo exemplos exagerados dos efeitos destas distorções na imagem final:
A biblioteca OpenCV oferece diversos recursos para realizar este processo de calibração. A partir da captura de múltiplas imagens de um objeto conhecido, é possível realizar uma estimativa dos parâmetros intrínsecos da câmera. Neste caso, o objeto utilizado foi um tabuleiro de xadrez impresso em uma folha de papel. O script calib.py agrega todas as imagens dentro da pasta ./images e encontra a posição do tabuleiro dentro da imagem em cada uma a partir da função findChessboardCorners fornecida pela biblioteca. Quanto maior o número de imagens utilizadas, melhor a precisão dos parâmetros encontrados, sendo recomendado um mínimo de 10 imagens. Após encontrar as posições dentro de cada imagem, a função calibrateCamera encontra a posição em 3D do tabuleiro em cada imagem assim como os parâmetros da câmera. Isto é feito com base em um processo similar ao realizado pelo programa, porém apresentando um número maior de variáveis, o que explica a necessidade por um número grande de imagens. O script em seguida armazena as medições no arquivo calib.npz que será usado pelo programa principal.
O primeiro passo realizado no processo envolve encontrar a posição dos marcadores dentro da imagem de entrada. O acesso à webcam é feito a partir do OpenCV e as imagens são retiradas do vídeo uma a uma em um loop. Cada imagem é então processada na busca de áreas que pareçam ser um dos marcadores luminosos. Ao fim deste passo é retornada uma lista de possíveis posições para os marcadores dentro da imagem.
Este processamento da imagem pode ser feito através da biblioteca pela classe SimpleBlobDetector. Ela pode ser configurada com informações como a cor dos marcadores, tamanho, formato, etc. Como versão inicial, esta classe foi utilizada dentro do programa na detecção dos marcadores. O trecho de código abaixo demonstra a utilização do SimpleBlobDetector dentro do programa:
params = cv2.SimpleBlobDetector_Params()
# Configuração do detector de pontos
params.minArea = min_area
params.maxArea = max_area
params.minThreshold = 160
params.maxThreshold = 255
params.filterByColor = True
params.blobColor = 255
# Criação do detector de pontos
detector = cv2.SimpleBlobDetector_create(params)
def detect(img):
# Converte para escala de cinza
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Encontra a posição de todos os pontos
keyp = detector.detect(gray)
imgp = [np.array(k.pt) for k in keyp]
return np.array(imgp)O algoritmo utilizado por esta classe pode ser descrito de forma simplificada da seguinte forma: primeiramente, a imagem em escala de cinza é separada em diversas fatias de acordo com o valor dos pixels. Em seguida, cada uma destas fatias sofre uma binarização de acordo com um intervalo de valores. A partir destas fatias binárias são encontrados todos os conjuntos de pixels contíguos presentes nelas. Finalmente, os conjuntos encontrados em cada fatia são unidos de acordo com a distância entre eles e filtrados de acordo com os parâmetros escolhidos.
Uma versão simplificada deste algoritmo também foi implementada completamente em Python como substituto. Nesta versão, a imagem em escala de cinza sofre uma única binarização de acordo com um valor mínimo fixo. De forma similar, nesta imagem binária são encontrados os conjuntos de pixels contíguos. Isto é feito usando um procedimento recursivo chamado flood fill, com funcionamento similar à ferramente balde de tinta do presente em programas como Paint e Photoshop. O algoritmo retorna o centro de massa de cada conjunto após filtrar de acordo com a área total, como visto no trecho abaixo:
def detect(img):
# Converte para escala de cinza
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Binarização da imagem
thresh = gray >= threshold
# Encontra todos os conjuntos de pontos contíguos
imgp = []
for y, x in np.ndindex(*thresh.shape):
if thresh[y, x]:
center, area = floodfill(thresh, x, y)
if min_area <= area <= max_area:
imgp.append(center)
return np.array(imgp)Também pode ser vista a implementação do procedimento flood fill no trecho em seguida. Esta implementação se utiliza de uma pilha explícita ao invés de recursão de forma a evitar o estouro da pilha:
def floodfill(img, x, y):
center = np.zeros(2)
area = 0
stack = [[x, y]]
for x, y in stack:
if not 0 <= x < img.shape[1]:
continue
if not 0 <= y < img.shape[0]:
continue
if not img[y, x]:
continue
img[y, x] = False
center += [x, y]
area += 1
stack.append([x, y-1])
stack.append([x, y+1])
stack.append([x-1, y])
stack.append([x+1, y])
center /= area
return center, areaEmbora o novo algoritmo apresente bom funcionamento em termos de encontrar os marcadores dentro da imagem, ele tem péssima performace por ser realizado em Python puro. Por isso, uma segunda versão precisou ser desenvolvida fazendo uso em parte da biblioteca OpenCV. A função findContours substitui o loop da versão anterior e encontra todos os conjuntos contíguos:
def detect(img):
# Converte para escala de cinza
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Binarização da imagem
thresh = (gray >= threshold).astype(np.uint8)
# Encontra todos os conjuntos de pontos contíguos
_, contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
imgp = []
for cont in contours:
center = np.average(cont, axis=0)[0]
area = len(cont)
if min_area <= area <= max_area:
imgp.append(center)
return np.array(imgp)Já esta nova versão do algoritmo apresenta performance adequada para o uso em tempo real.
Ao fim do passo anterior foi encontrada uma lista de posições dentro da imagem. Estas posições correspondem a possíveis marcadores, porém também podem ser meramente ruído. Além disso, não sabemos qual posição na imagem corresponde a qual marcador no nosso objeto. Antes que a estimativa da posição possa ser realizada, é necessário determinar não só quais posições dentro desta lista são marcadores ou não, mas também exatamente qual dos marcadores está associado a esta posição.
Dentro do campo de visão computacional este tipo de problema é bastante comum, por isso existem diversos algoritmos que buscam determinar esta associação. A maioria destes algoritmos se baseia em resolver o problema de forma iterativa, testando diferentes combinações para subconjuntos de pontos e melhorando a solução a cada passo. Algoritmos deste tipo são essenciais quando o número de pontos é muito grande, já que o número de combinações possíveis é gigantesco. Porém, para esta aplicação algoritmos mais simples já bastam dado que o número de pontos é bem pequeno.
Uma solução simples se baseia em impor restrições na posição do objeto em relação à câmera. Nesta primeira versão do algoritmo, é assumido que o objeto está virado em direção à câmera e sua rotação é pequena. Assim, podemos considerar que o objeto está orientado aproximadamente de pé. Além disso, os marcadores assumem uma configuração de retângulo, estando posicionados nas quatro pontas deste retângulo. Tomamos então os pontos sempre na seguinte ordem de acordo com sua posição na imagem: inferior esquerdo, inferior direito, superior esquerdo, e superior direito:
def order(keyp):
# Utiliza apenas 4 pontos
keyp = keyp[:4]
imgp = [k.pt for k in keyp]
# Ordena todos pela coordenada y (de baixo pra cima)
imgp.sort(key=lambda p: -p[1])
# Ordena pares pela coordenada x (da esquerda pra direita)
imgp[:2] = sorted(imgp[:2], key=lambda x: x[0])
imgp[2:] = sorted(imgp[2:], key=lambda x: x[0])
return np.array(imgp)Embora este algoritmo resolva o problema de maneira simples, ele apresenta dois grandes problemas. Um dos problemas é que, pela própria construção do algoritmo, a posição do objeto sofre restrições em relação à sua orientação. Outro problema é que a distribuição dos marcadores fica restrita ao modelo escolhido, com quatro pontos em formato de retângulo. Para tratar estes problemas uma segunda solução foi desenvolvida.
Nesta solução, a posição anterior dos marcadores é usada para encontrar a nova associação. A cada nova imagem, a posição dos pontos encontrados é comparada à posição dos marcadores na imagem anterior. Assim, os pontos que se encontram mais próximos aos marcadores na imagem anterior serão associados entre si. Como na maior parte das vezes o objeto não se move muito entre uma imagem e outra, este algoritmo costuma encontrar a correspondência correta entre a posição dos pontos e os marcadores:
def order(keyp, rvec, tvec, cmat, dist):
# Calcula a projeção dos marcadores na imagem anterior
imgp_last, _ = cv2.projectPoints(objp, rvec, tvec, cmat, dist)
# Encontra o ponto mais próximo para cada marcador
imgp = []
for p in imgp_last:
i = np.linalg.norm(keyp - p, axis=1).argmin()
q = keyp[i]
imgp.append(q)
return np.array(imgp)Embora este algoritmo funcione na maioria dos casos, às vezes a associação encontrada está errada. Além disso, o algoritmo depende de uma solução anterior para a posição do objeto, por isso é necessário encontrar uma associação de outra maneira quando uma solução anterior não estiver disponível. Para isso, caso o algoritmo falhe também são escolhidas um número de associações aleatórias a cada imagem:
# Encontra a posição de todos os pontos
keyp = detect(img)
[...]
imgps = []
# Utilizar solução anterior caso exista
if flag:
imgp = order(keyp, rvec, tvec, cmat, dist)
imgps.append(imgp)
# Também escolher `num_guess` associações aleatórias
for _ in range(num_guess):
i = np.random.choice(len(keyp), len(objp))
imgp = keyp[i]
imgps.append(imgp)
# Descarta associações inválidas (contêm pontos muito próximos)
imgps = [p for p in imgps if valid(p)]Agora que obtemos a posição dos marcadores na imagem, já temos todas as informações necessárias para estimar a posição do objeto. Com base no modelo de câmera pinhole descrito anteriormente, assim como os coeficientes de distorção, podemos então encontrar os vetores de rotação e translação que descrevem a posição do objeto no espaço 3D. Em visão computacional este problema é conhecido como Perspective-n-Point ou simplesmente PnP, isto é, encontrar a posição em 3D de um conjunto de n pontos com base em suas projeções em 2D.
Embora seja baseado em coordenadas homogêneas, o sistema descrito pelo modelo de câmera pinhole é não-linear, já que envolve projeções. Além disso, as distorções introduzidas pela câmera e medidas no passo de calibração também são não-lineares. Por conta disso a solução pode ser encontrada através de métodos iterativos, como por exemplo o gradiente descendente. A biblioteca também oferece ferramentas para resolver este tipo de problema, como por exemplo a função solvePnP, que recebe a posição dos pontos relativas ao objeto, suas projeções, e os parâmetros intrínsecos da câmera, retornando os vetores de rotação e translação:
ret, rvec, tvec = cv2.solvePnP(objp, imgp, cmat, dist)A método escolhido para a solução deste problema é similar ao método de Gauss-Newton. O algoritmo busca resolver um problema de mínimos quadrados de forma iterativa. Neste caso, o erro é medido entre as projeções dos pontos encontradas na imagem e da estimativa. O problema pode ser descrito de forma geral da seguinte maneira:
Onde x representa as coordenadas dos pontos em 3D, y suas projeções em 2D, f o modelo da câmera pinhole com distorções, e β a posição do objeto (vetores de rotação e translação). Assim, f pode ser aproximado em primeira ordem da seguinte maneira:
Onde J é a jacobiana de f. A partir desta aproximação, o erro também pode ser aproximada de acordo com a seguinte equação:
Podemos então manipular esta equação em sua forma vetorial:
Queremos encontrar o mínimo desta equação. Para isso, tomamos a derivada de S(β + δ) em relação a δ e igualamos a zero. A solução desta nova equação irá determinar qual passo deve ser tomado para minimizar o erro nesta versão linearizada do problema:
Como o problema é não-linear, este passo é repetido de forma iterativa até que o erro alcance a tolerância desejada. Como forma de melhorar a estabilidade do método, também é introduzido um fator de amortecimento λ que controla o comportamento da iteração. Para fatores λ próximos de zero, a iteração é feita através do método de Gauss-Newton. Já para fatores maiores, a iteração segue a direção do gradiente e se aproxima cada vez mais do método gradiente descendente:
Além disso, por ser um método iterativo, o algoritmo necessita de um chute inicial como ponto de partida. Quanto melhor o chute, mais rápido o algoritmo converge para a solução. Como explorado anteriormente, sabemos que o objeto não se move muito entre uma imagem e outra. Por isso, a posição anterior do objeto é utilizada como chute inicial quando uma solução anterior está disponível. Desta forma, o método converge em poucos passos (por volta de 2) nestes casos.
A projeção da estimativa usada no cálculo do erro é obtida através da função projectPoints da biblioteca. Esta função também retorna a jacobiana utilizada em cada iteração. O trecho a seguir implementa o método descrito:
def solvepnp(objp, imgp, cmat, dist, rvec, tvec, flag):
imgp = imgp.flatten()
# Constrói o vetor posição a partir dos vetores de rotação e translação
if flag:
vecs = np.concatenate((rvec, tvec))
# Caso a solução anterior não esteja disponível, escolhe valores padrão
else:
vecs = np.concatenate((default_rvec, default_tvec))
# Limite máximo de 30 iterações
for i in range(30):
rvec, tvec = vecs[:3], vecs[3:]
# Projeta a estimativa e calcula a jacobiana
p, jac = cv2.projectPoints(objp, rvec, tvec, cmat, dist)
p, jac = p.flatten(), jac[:,:6]
# Retorna caso o erro seja menor que a tolerância desejada
rloss = np.linalg.norm(imgp - p) / np.linalg.norm(imgp)
if rloss < rtol:
print(i+1, 'iters')
return True, rvec, tvec
a = jac.T.dot(jac) + damping * np.eye(6)
b = jac.T.dot(imgp - p)
# Realiza uma iteração do método
try:
dvec = np.linalg.solve(a, b)
vecs += dvec
# Em caso de sistema singular escolhe outro chute incial
except:
rvec[:] = default_rvec + np.pi * np.random.rand(3)
tvec[:] = default_tvec + np.random.randn(3)
return False, rvec, tveccalib.py: Realiza a calibração da câmeratracker.py: Módulo principal do programadetect.py: Funções de detecção de marcadoressolvepnp.py: Funções de estimativa de posiçãographics.py: Wrapper para a renderização gráfica com OpenGL/data: Recursos gráficos/images: Armazena as imagens para calibração
Python3, numpy, opencv-python, pygame, PyOpenGL, pyassimp