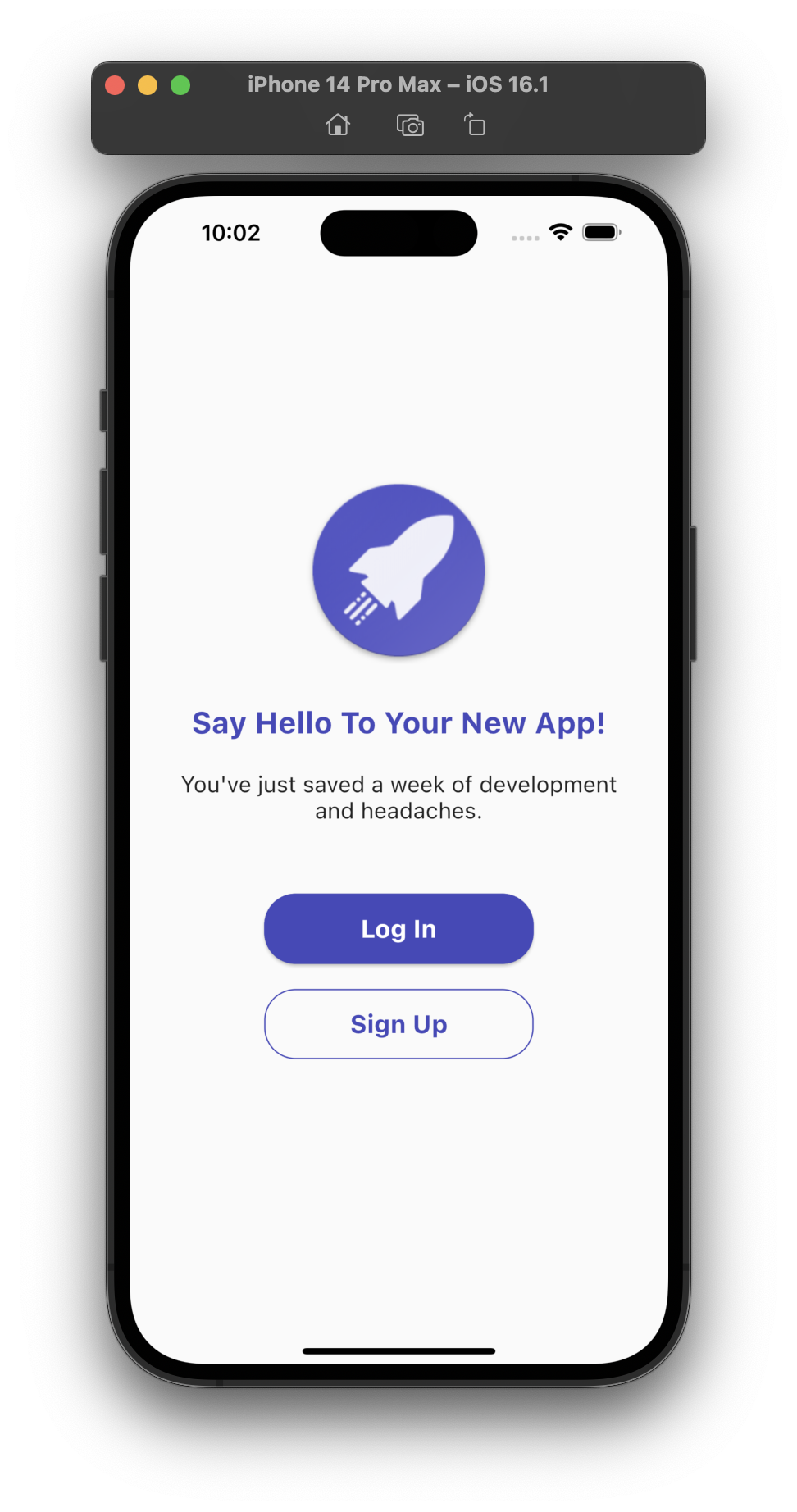
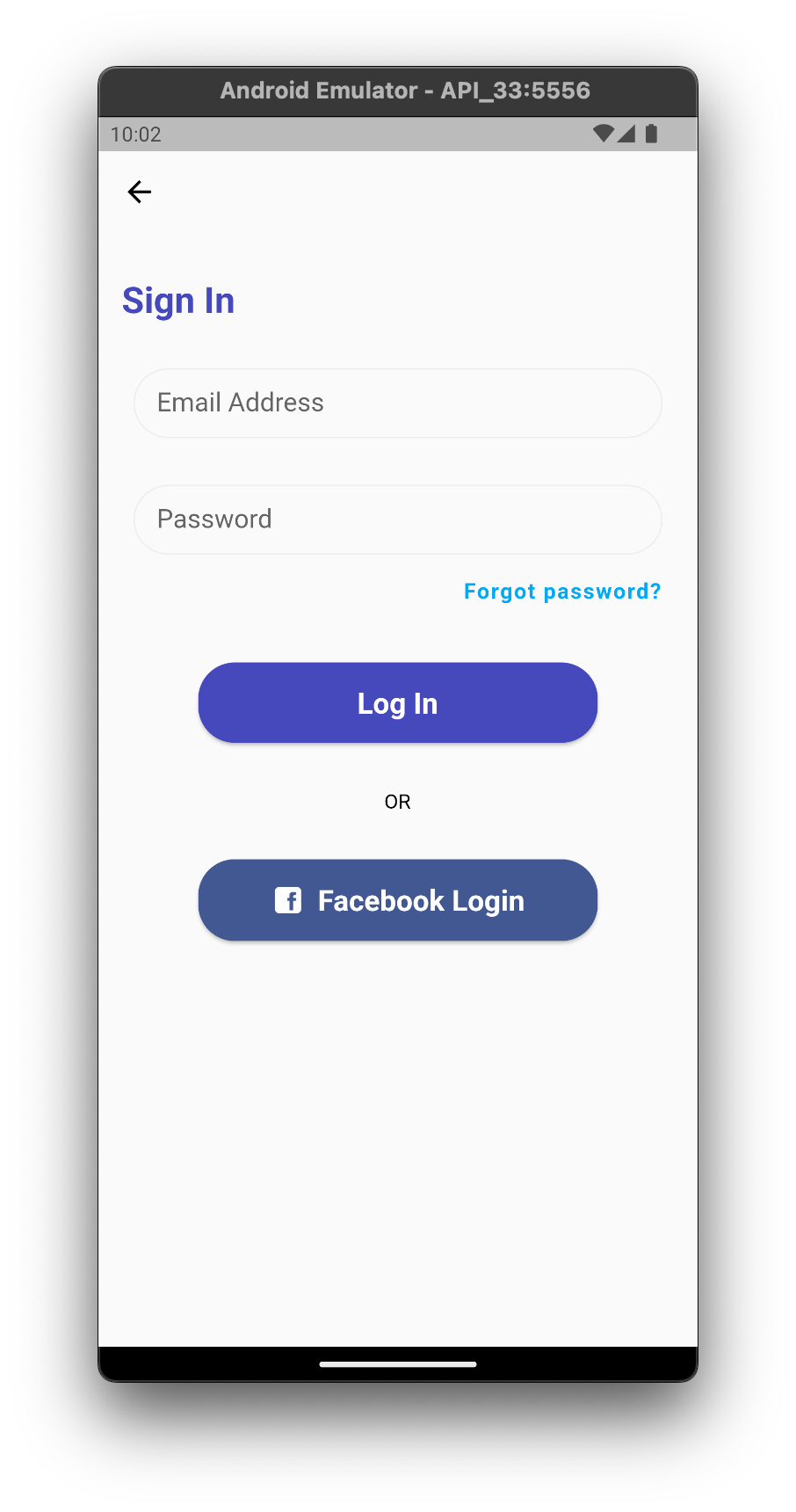
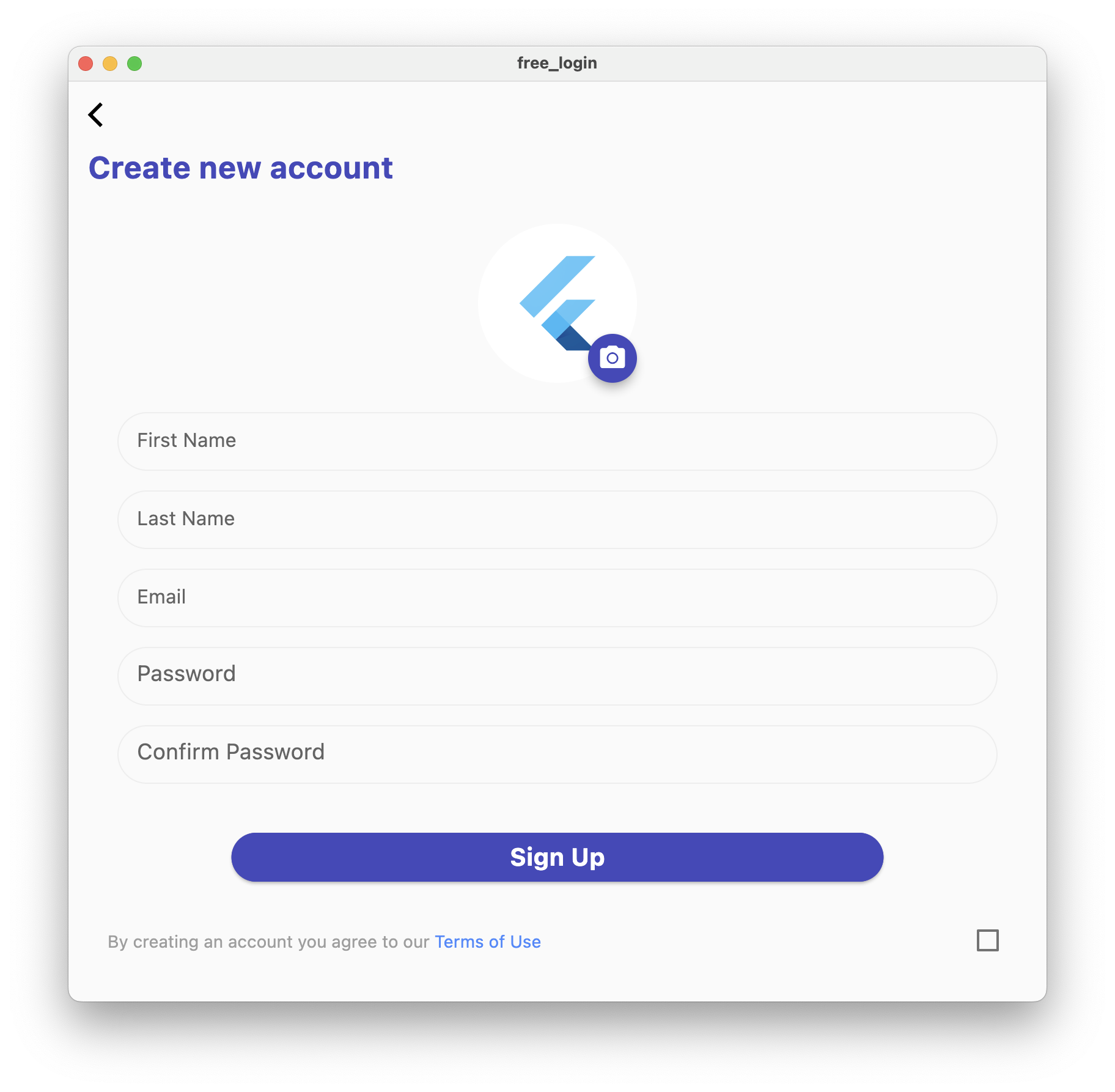
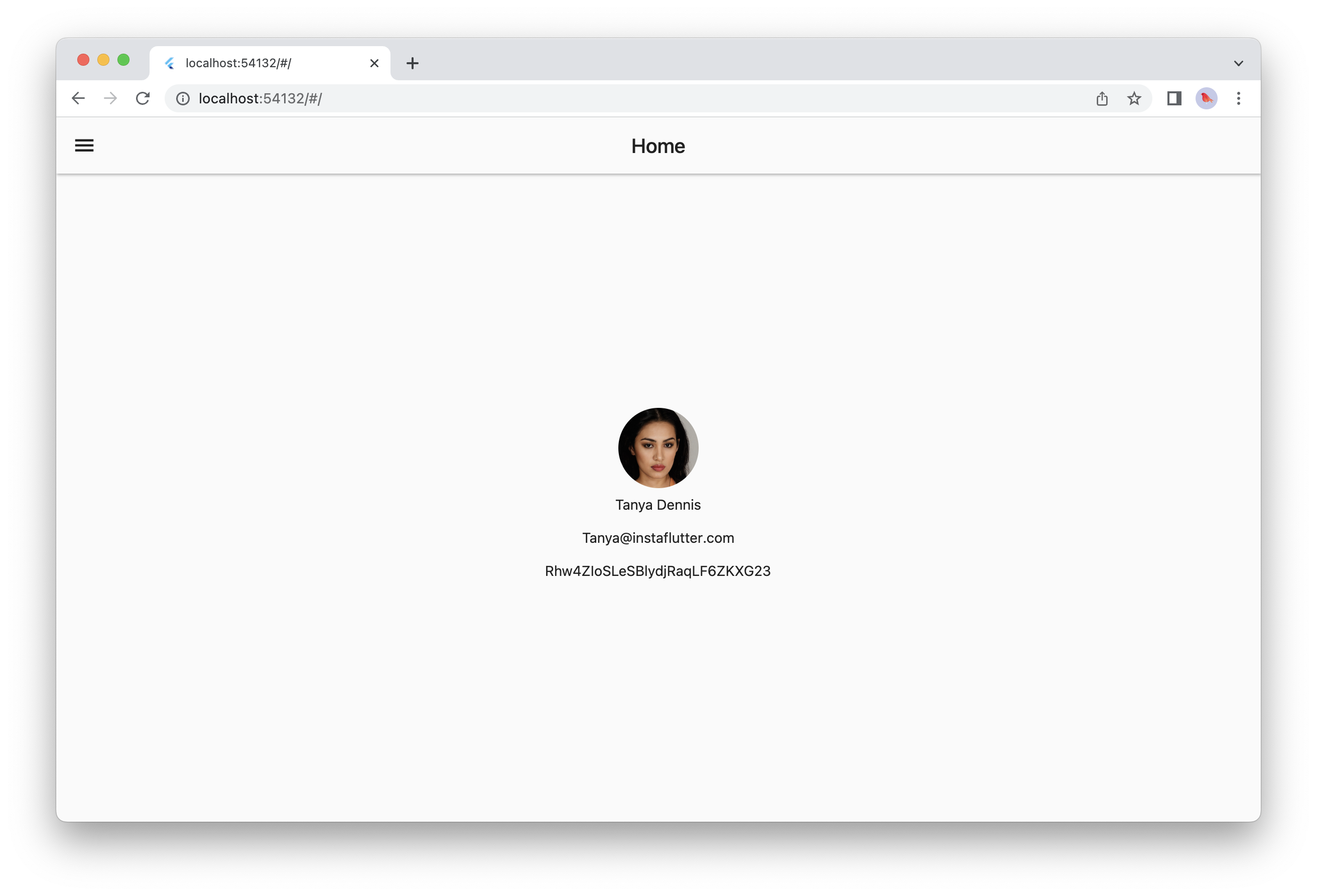
Jumpstart your Flutter app development with this pre-built Flutter starter kit. Don't reinvent the wheel by writing the boring boilerplate starter code. Jump straight into the action and focus strictly on your core app features, if you want a detailed guide on how you can connect your Flutter app to firebase, feel free to checkout our detailed guide: https://www.instaflutter.com/docs/documentation/firebase-integration/.
Instaflutter Onboarding is a fully functional app that provides Flutter developers with a coded template for their mobile app projects. It has a great number of popular features:
- Cross platform support (Android, iOS, Web and macOS)
- Firebase Auth integration
- Login with Facebook
- Login with Apple
- Login with e-mail & password
- Persistent Login Credentials
- Visual Error Handling
- Firebase Firestore integration
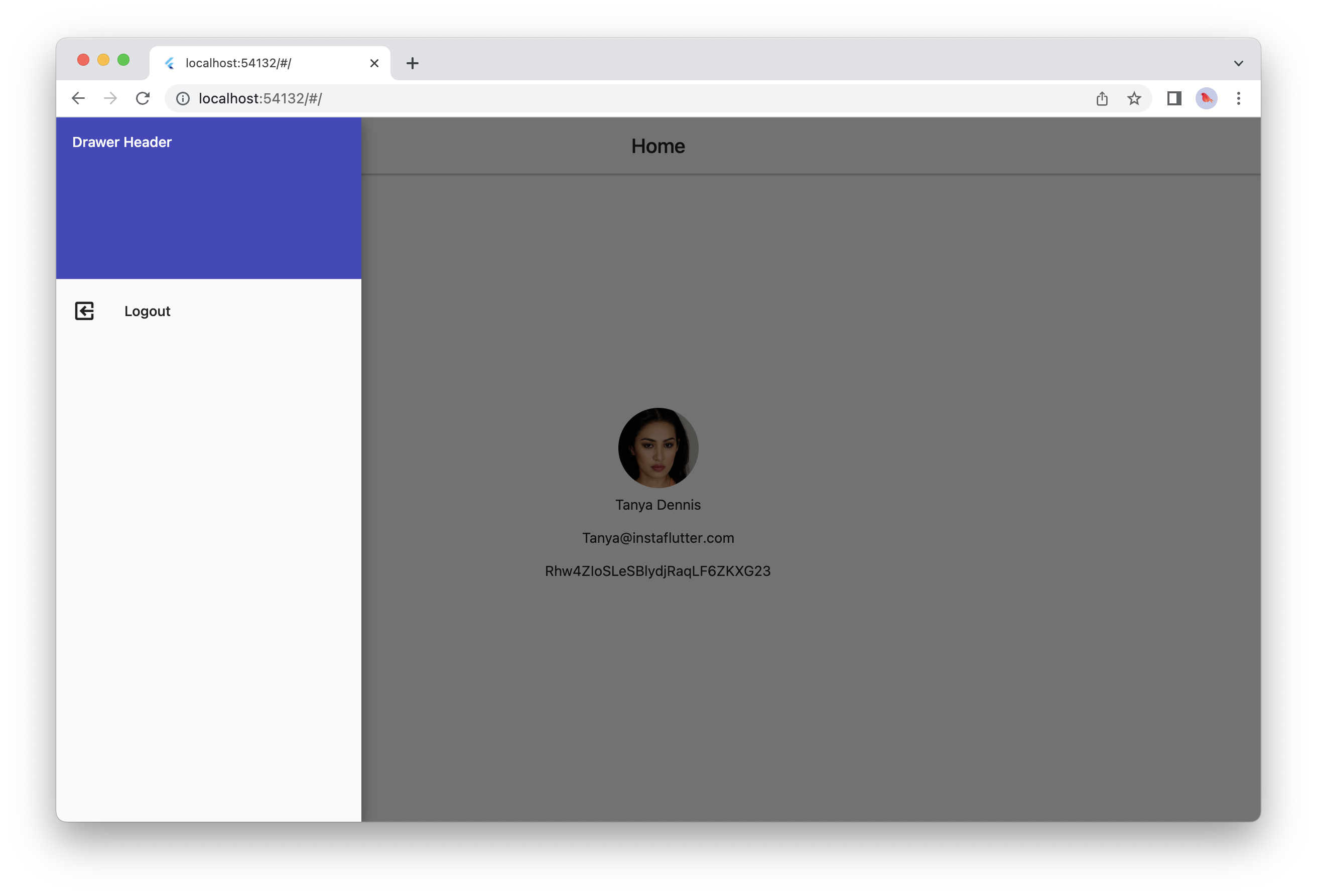
- Logout Functionality
- Profile Photo Upload
- Firebase Storage integration
- Walkthrough flow
- Welcome Screen
- Login Screen
- Forgot password Screen
- Sign up Screen
- Home Screen
- Navigation Drawer
- Beautiful UI
- Optimized for both iOS and Android
- Modularized Code
- Loading States
- Error Handling
- flutter clean
- flutter pub get
- flutter pub run build_runner build (not in this code but others)
- flutter run
- Follow this tutorial
https://youtu.be/_3W-JuIVFlg - Read this article
https://instaflutter.com/docs/documentation/firebase-integration/enable-firebase-storage/for setting up the storage component for uploading data like profile pictures & audio/video to firebase
Coded with ❤️ by Instaflutter.
To calculate the odds of winning the lotto, we need to determine the total number of possible combinations and the number of winning combinations.
In this case, you are picking 6 numbers from a range of 1 to 59.
The total number of possible combinations can be calculated using the formula for combinations:
C(n, k) = n! / (k! * (n - k)!)
Where: n = total number of choices (59 in this case) k = number of choices to be made (6 in this case)
Using this formula, the total number of possible combinations is:
C(59, 6) = 59! / (6! * (59 - 6)!)
The number of winning combinations is simply 1 since there is only one winning combination.
Therefore, the odds of winning the lotto with these parameters are:
1 / (59! / (6! * (59 - 6)!))
To calculate the actual numerical value, you would need to evaluate this expression using a calculator or programming language with support for large numbers.
If you are picking 5 numbers from a range of 1 to 39, we can calculate the odds of winning the lotto by following a similar approach as before.
The total number of possible combinations can be calculated using the combination formula:
C(n, k) = n! / (k! * (n - k)!)
Where: n = total number of choices (39 in this case) k = number of choices to be made (5 in this case)
Using this formula, the total number of possible combinations is:
C(39, 5) = 39! / (5! * (39 - 5)!)
The number of winning combinations is still 1.
Therefore, the odds of winning the lotto with these parameters are:
1 / (39! / (5! * (39 - 5)!))
To calculate the actual numerical value, you would need to evaluate this expression using a calculator or programming language with support for large numbers.
To evaluate the expressions:
1 / (59! / (6! * (59 - 6)!))
1 / (39! / (5! * (39 - 5)!))
we can use a calculator or a programming language to compute the actual values.
The first expression evaluates to approximately 1 in 45,057,474.
The second expression evaluates to approximately 1 in 575,757.
To determine the difference in odds between the two, we can calculate the ratio of the second odds to the first odds:
(1 / (39! / (5! * (39 - 5)!))) / (1 / (59! / (6! * (59 - 6)!)))
Simplifying this expression gives us:
(59! / (6! * (59 - 6)!)) / (39! / (5! * (39 - 5)!))
Evaluating this ratio gives us a value of approximately 1297.37.
Therefore, the odds of winning the lotto are approximately 1297.37 times greater when picking 5 numbers from a range of 1 to 39 compared to picking 6 numbers from a range of 1 to 59.