179 Tangrams is a browser implementation of the classic Chinese puzzle using plain JavaScript(no packages) and the Canvas API. The puzzle consists of seven polygons tiles, which are put together to form shapes. The objective is to replicate a given pattern using all seven tiles without overlap.
A dimension that is unique to this implementation of Tangram is that the player is scored by how quickly he/she can solve a puzzle. A timer automatically starts when the player enters a level and is only stopped whenever the user exits (by hitting pause, or switching tabs) or when the puzzle is solved. This added timing component means that the program would need a quick and cheap way to constantly check whether the puzzle had been solved.
For the aforementioned task, a raster based overlap detection algorithm was developed. The approach involves painting the silhouette and tiles onto a secondary canvas, making sure the two entities are centered with respect to one another, and then counting the non-overlapping pixels on the silhoutte.
The screenshot below shows live gameplay with the secondary canvas overlayed on top. As the tiles on the main canvas moves, the secondary canvas is also updated. The green counter is a live reading of sum of total number of non-overlapping silhouette pixels. Notice that when the when the probem solved, the green coutner drops to below 6000, which is the solve threshold, and the timer stops.
We start out painting the silhouette then the tangram tiles on a secondary canvas that is off-screen. By ensuring that the geometric centers of the silhouette and the tangram tiles align, it follows that there is maximum overlap between the tangram tiles and the silhouette when the puzzle is solved. Conversely, this means that the non-overlapping areas of the silhouette is at a minimum.
To detect this solved state, we set both the background and the tile to black (rgb(0,0,0)) while the silhouette set to any non-black color which in our case was cyan, most importantly with a red color value of 1, rgb(1,255,255). Since the tangrams shapes are painted after the silhouette, any overlapping areas will be set to black, whereas the non-overlapping areas of the silhouette remain cyan.
After every tile move, the program sums the red pixel values of all the pixels on the secondary canvas (using CanvasRenderingContext2D.getImageData()). Since we had set the silhouette to have a red color value of 1, the sum is also the number of pixels of silhouette that is non-overlapping. If the non-overlap pixel count is below a certain threshold (empirically determined), we can conclude that the player has solved the puzzle.
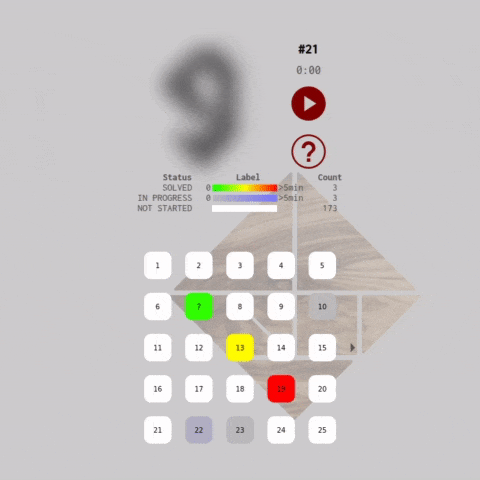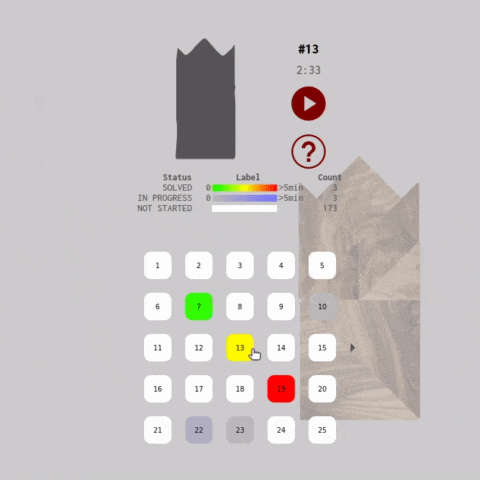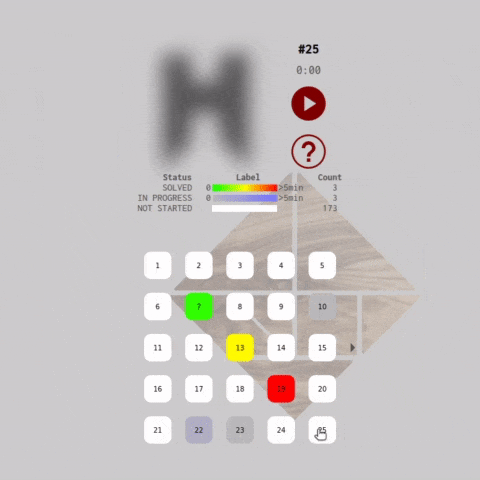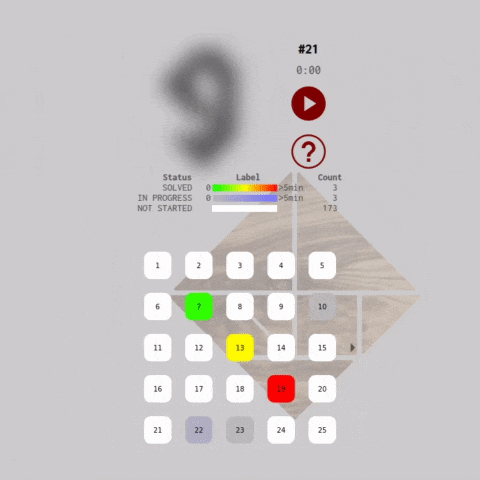
As the use hover the mouse over each problem icon in the carousel, the game canvas updates with a preview of the problem and the current state of the tiles in that level. The silhouette for unsolved problems are blurred in the preview to prevent the player from getting a head start before starting the timer.
To allow for smooth transition between pages, the carousel utilizes a Bezier easing function to generate the snapping animation to the nearest page.
The carousel also functions as a heat map that tracks the player's progress. The heat maps colors each level icon depending on elapsed time and the puzzle solve state. The heatmap is generated by formatting an HSL color string with the which becomes an attributes of a SVG <rect> element.
The heat map adds a badge-like reward mechanism to the gameplay experience. The user may be motivated to fill up the entire carousel with green boxes :)
Adding realism to the game play, the program checks for collision between the puzzle tiles. After each tile move, if there is a collision, the penetration amount between the penetrating vertex and the penetrated edge is calculated.
Before we can calculate the penetration amount, we first need to find all the vertices that have penetrated another polygon by iterating through each vertex polygon combination possible (with some pruning) running the following function.
Note: All points and vectors in the format of a length 2 array [x-component,y-compoent],
export const toVec = (a, b) => [b[0] - a[0], b[1] - a[1]];
export const cross = (v, w) => v[0] * w[1] - v[1] * w[0];
export function insidePoly(vertices, p) {
// checks if point p in located inside polygon with def by the vertices argment
// important!! this assumes vertices are arranged in counter clockwise order
let left = vertices[vertices.length - 1];
for (let i = 0; i < vertices.length; i++) {
const center = vertices[i];
if (cross(toVec(center, left), toVec(center, p)) > 0) {
return false;
}
left = center;
}
return true;
}After we identify the penetrating vertice / penetrated polygon pair, we check the penetrating vertex's latest path segment (defined by its last two recorded positions) for intersection with each edge of the penetrated polygon. Knowing the penetrating vertex and penetrated edge, we calculate the the perpendicular component between them. This perpendicular vector is exactly how much the vertex has penetrated the polygon. The code snippet for this procedure is pasted below. Note that calcPenetration() calls findIntersection()
export function findIntersection(p, r, q, s) {
/*
Based on: https://stackoverflow.com/questions/563198/
q+s p+r
\/__________ q+u*s
/\
/ \
p q
u = (q − p) × r / (r × s)
when r × s = 0, the lines are either colinear or parallel
function returns u
for intersection to exist, 0<u<1
*/
const q_minus_p = toVec(p, q);
const r_cross_s = cross(r, s);
if (r_cross_s === 0) return null;
return cross(q_minus_p, r) / r_cross_s;
}
export const dot = (v, w) => v[0] * w[0] + v[1] * w[1];
export function calcPenetration(sVertices, p, lastMouseMove) {
/*
determine if last mouse move caused a state change for point p
from no penetration to penetration into shape s (represented by sVertices)
if such state change occured, return the penetration vector
if not, this return null
*/
let prev = sVertices[sVertices.length - 1];
// scale last mouse move vector by 20%, empirically this has been found to help
// with interseciton detection sensitivity
lastMouseMove = lastMouseMove.map(ele => ele * 1.2);
// iterate through each polygon edge, return if penetration is encountered
for (let k = 0; k < sVertices.length; k++) {
const currVertex = sVertices[k];
const edgeVec = toVec(currVertex, prev); // vector respresenting current polygon edge
const res = findIntersection(currVertex, edgeVec, p, lastMouseMove)
if (res
&& res > 0 // res==0, when p started on on the polygon edge
&& res < 1 // res==1, when p is on polygon edge after mouse move
) {
// point indeed penetrated the current polygon edge
// calculate and return perpendicular component between p and the polygon edge
const p_currVertex_vec = toVec(p, currVertex); //
const precalc = dot(p_currVertex_vec, edgeVec) / (edgeVec[0] ** 2 + edgeVec[1] ** 2);
return p_currVertex_vec.map((ele, idx) => ele - precalc * edgeVec[idx]);
}
prev = currVertex;
}
return null;
}Knowing this penetration vector, the moving tile is then shifted back by the this exact amount, ensuring that the tiles are just touching, but not intersecting
Instead of generating the problem manually, examples of Tangram problems found online were leveraged. The 179 puzzles in this game was taken from a puzzle booklet first published in 1890 by the Richter Company of Germany in 1890. The problems were extracted from scanned images of the puzzle booklet with a python script using OpenCv's findContours().
- User generated levels
- Public high score leader board