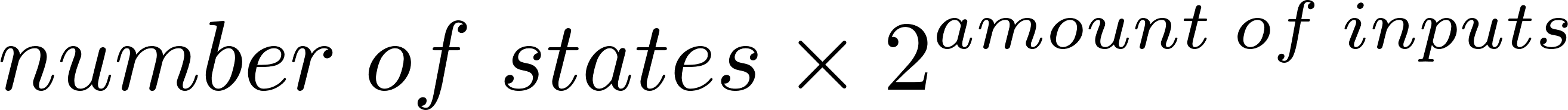The project consists of elaborating a system that graphically simulates a Finite State Machine described by the user, whether is it Mealy or Moore. It supports up to 8 states and from this it is able to generate the diagram that receives the input desired by the user at a given state. In the header it is possible to generate a report with the outputs generated in that FSM following the entries chosen and update the current state also according to the entry.
As well the system informs, by each transition, the previous state, the ongoing state, and the output and generates a final report with the states covered, the inputs received and the sequence of outputs.
The project was developed using HTML technologies to structure the page that receives the data from the machine described by the user, CSS to stylize the page that reads the data and JavaScript (along with the jQuery library) to manipulate it, generate the state machine and perform click events.
To assist the graphical interface,we used canvas that is an element of HTML5 that can be manipulated through JavaScript, in addition, we use a graphic library that allows the generation of circles from positions (x, y) and also allows the creation of arrows, to represent the transitions.
The code consists of the HTML implementation of the form that receives the user information, in addition to the JS code that is responsible for selecting and saving the data entered by users into variables. Finally, as the main part, the project also contains the code responsible for, from the number of states and their future states, generate the circles and arrows, once all the coordinates are defined previously, being only necessary to decide whether to display each information, futhermore, it has the event of the input buttons, which from the current state and the input clicked, traverses a array containing the table with states and future states, and lastly decides which state to transition.
The project's goal was achieved being possible to generate the state diagram from the description of a FSM, however, it was necessary to define some limitations in the system, they are:
- Number of States
Its upper bound is 8, since the creation of circles representing the states are manually defined in the code and with a bigger amount of it the space of the canvas would be more fully filled so it could be more difficult to extract information from it.
- Number of Input and Output bits
They are limited to only one, such measure has been taken since increasing the number of inputs and outputs, causes the number of information passed by the user to increase greatly, following the formula:
This would cause many arrows to be added, because there'd be the possibility that from given state the transitions take place up to 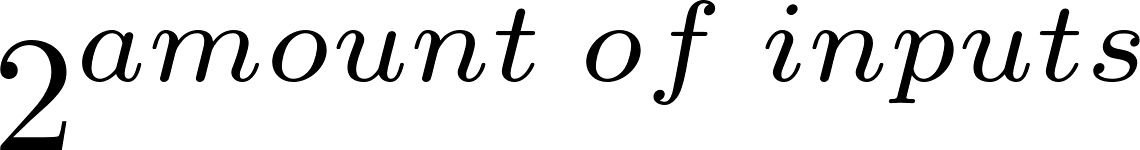 other states
other states
Open this link or clone or download this project then open trab.html.
The use of the system basically consists of the way in which the user must enter the information related to the desired state machine diagram, it is necessary to fill in the following data:
- Type of Machine;
- Amount of States;
- Table with current state, input, future state and output in each line.
The formatting used for the table should follow these rules: Each state must be informed with the number that represents the state, in decimal format, the first state being represented by the number 1 and the last state by the number 8. Therefore, each line of the table must contain the number that represents the current state, followed by a space and the bit zero or one to represent the input that will lead to the next state, which must be typed next and finally:
- if it's a Mealy machine, the output bit that occurs in the transition;
- or if it's a Moore machine, the output bit of that state.
Note that for Moore machines, outputs of equal future states must be equal.
Some input exemples can be found at InputExemples.txt.
Eduardo Alves Baratela - 10295270
Fabio Fogarin Destro - 10284667
Paulo André de Oliveira Carneiro - 10295304
Vitor Henrique Gratiere Torres - 10284952
Digital Systems
Institute of Mathematical and Computer Sciences
University of São Paulo
Professor Mauricio Acconcia Dias
2017.2