The name Spreads stands for Series and Panels for Real-time and Exploratory Analysis of Data Streams.
- Data streams are unbounded sequences of data items, either recorded or arriving in real-time;
- Series are navigable ordered data streams of key-value pairs;
- Panels are series of series or data frames;
- Exploratory data transformation in C#/F# REPLs;
- Real-time fast incremental calculations.
Spreads is an ultra-fast library for complex event processing and time series manipulation. It could process tens of millions items per second per thread - historical and real-time data in the same fashion, which allows to build and test analytical systems on historical data and use the same code for processing real-time data.
Spreads is a library, not a framework, and could be plugged into existing code bases and used immediately. Even though the primary domain is financial data, Spreads was designed as a generic complex event processing library, with a performance requirement that it must be suitable for ticks and full order log processing. This is probably the largest data stream that cannot be meaningfully sharded: financial instruments are all directly or indirectly correlated and we need to monitor markets as a whole while Google/Facebook and similar user event streams could be processed independently.
Spreads library is optimized for performance and memory usage. It is several times faster than other open source projects, does not allocate memory for intermediate calculations or windows, and provides real-time incremental calculations with low-latency lock-free synchronization between data producers and consumers. You could run tests and benchmarks to see the exact numbers.
For regular keys - keys that have equal difference between them (e.g. seconds) - Spreads stores
only the first key and the step size, reducing memory usage for <DateTime,T> data item by
8 bytes. So <DateTime,double> data item takes only 8 bytes inside Spreads series instead of 16.
The gains of this optimization are not obvious on microbenchmarks with a single
series, and one could argue that memory is cheap. However, L1/L2/L3 caches
are still small, and saving 50% of memory allows to place two times
more useful data in the caches and to avoid needless cache trashing.
Spreads library is written in C# and F# and targets .NET 4.5.1 and .NET Standard 1.6 versions. .NET gives native performance when optimized for memory access patterns, which means no functional data structures and minimum allocations. Even though .NET is a managed platform with garbage collection, in a steady state Spreads should not allocate many objects and create GC pressure. .NET properly supports generic value types and arrays of them are laid out contiguously in memory. Such layout enables CPUs to prefetch data efficiently, resulting in great performance boost compared to collections of boxed objects. Also .NET makes it trivial to call native methods and Spreads.Core project uses SIMD-optimized compression and math libraries written in C.
We haven't compared Spreads performance to performance of commercial systems yet (because their costs are atrocious and learning cryptic languages is not necessary). However, the main benchmark while developing Spreads was modern CPUs capabilities, not any existing product. We tried to achieve mechanical sympathy, to avoid any wasteful operations and to get the most from modern processors. Therefore, unless the fastest commercial products use magic or quantum computers, Spreads must be in the same bracket.
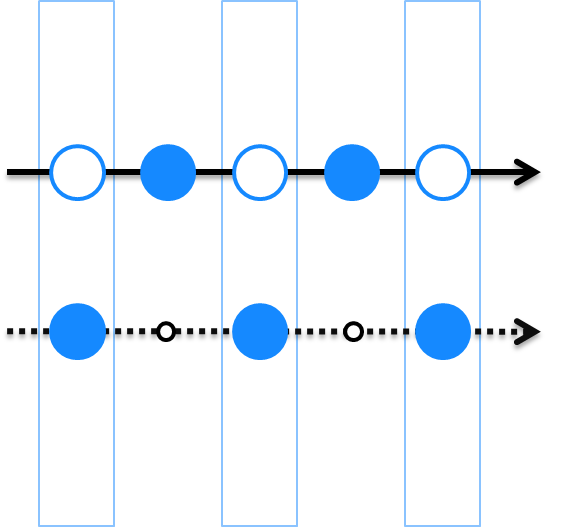
Series could be continuous or discrete. Continuous series have values at any key, even between observed keys. For example, linear interpolation or cubic splines are continuous series defined from observed points. Another example is "last price", which is defined for any key as observed price at or before the key.
Discrete series have values only at observations/events, e.g. trade volume
is meaningful only at observed trades, there is no implied latent volumes between trades. We could
create a derived continuous series, e.g. let liquidity = volume.SMA(N).Repeat(), but this
series changes meaning from a real observed volume to an abstract analytical indicator of average
liquidity over the last N observations.
On pictures, a solid line means continuous series, dotted line means discrete series, solid blue dot means an observation, a white dot with blue outline means a calculated value of a continuous series at a key between observations.
One of the core feature of Spreads library is declarative lazy series manipulation.
A calculation on series is not performed until results are pulled from Series. For example,
expression let incremented = series + 1.0 is not evaluated until incremented series
is used. Instead, it returns a calculation definition that could be
evaluated on demand.
Missing values are really missing in Spreads, not represented as a special NA or option value. When missing values are present as special values, one need to spend memory and CPU cycles to process them (and a lot of brain cycles to comprehend why missing values are somehow present, and not missing).
One of the most frequently used series transformations are Repeat and Fill. Calling them
on a discrete series returns a continuous series, where for each non-existing key we could get
a value from the key at or before requested key for Repeat or a given value for Fill:
let repeated = sparseSeries.Repeat()
let filled = sparseSeries.Fill(0.0)
The returned series contains infinite number of values defined for any key, but the values from non-observed keys are calculated on demand and do not take any space.
ZipN functionality is probably the most important part in Spreads.Core and it is shown on Spreads logo. ZipN supports declarative lazy joining of N series and in many cases replaces Frames/Panels functionality and adds real-time incremental calculations over N joined series.
All binary arithmetic operations are implemented via ZipN cursor with N=2. ZipN alway produces inner join, but it is very easy to implement any complex outer join by transforming an input series from a discrete to a continuous one.
For example, imagine we have two discrete series (in pseudocode) let upper = [2=>2; 4=>4]
and let lower = [1=>10; 3=>30; 5=>50] that correspond to the picture. If we add them via + operator,
we will get an empty series because there are no matching keys and inner join returns an empty set.
But if we repeat the upper series, we will get two items, because the
repeated upper series is defined at any key:
let sum = upper.Repeat() + lower // [3=>2+30=32; 5=>4+50=54]
If we then fill the lower series with 42, we will get:
let sum = upper.Repeat() + lower.Fill(42.0) // [2=>2+42=44; 3=>2+30=32; 4=>4+42=46; 5=>4+50=54]
For N series logic remains the same. If we want to calculate a simple price index like DJIA
for each tick of underlying stocks, we could take 30 tick series, repeat them (because ticks are irregular), apply ZipN
and calculate average of prices at any point:
let index30 : Series<DateTime,double> =
arrayOfDiscreteSeries
.Map(fun ds -> ds.Repeat())
.ZipN(fun (k:'DateTime) (vArr:'double[]) -> vArr.Average())
The values array vArr is not copied and the lambda must not return anything that has a
reference to the array. If the arrays of zipped values are needed for further use outside
zip method, one must copy the array inside the lambda. However, this is rarely needed,
because we could zip outputs of zips and process the arrays inside lambda without allocating
memory. For example, if we have series of returns and weights from applying Zip as before,
these series are not evaluated until values are requested, and when we zip them to calculate
SumProduct, we will only allocate two arrays of values and one array or arrays (pseudocode):
let returns = arrayOfPrices
.Map(fun p -> p.Repeat())
.ZipN(fun k (vArr:double[]) -> vArr)
.ZipLag(1,(fun (cur:double[]) (prev:double[]) -> cur.Zip(prev, (fun c p -> c/p - 1.0)))) // the last zip is on arrays, must be eager
let weights = arrayOfWeights
.Map(fun p -> p.Repeat())
.ZipN(fun k vArr -> vArr)
let indexReturn =
returns.ZipN(weights.Repeat(), (fun k (ret:double[]) (ws:double[]) -> SumProduct(ret, ws))
Here we violate the rule of not returning vArr, because it will be used inside lambda of ZipLag, which applies lambda to current and lagged values and does not returns references to them. But for this to be true, Zip of arrays must be eager and we will have to allocate an array to store the result. We could change the example to avoid intermediate allocations:
let returns = arrayOfPrices
.Map(fun p -> p.Repeat())
.ZipN(fun k (vArr:double[]) -> vArr)
.ZipLag(1,(fun (cur:double[]) (prev:double[]) -> ValueTuple(cur,prev)))
let weights = arrayOfWeights
.Map(fun p -> p.Repeat())
.ZipN(fun k vArr -> vArr)
let indexReturn =
returns.ZipN(
weights.Repeat(),
(fun k (ret:ValueTuple<double[],double[]>) (ws:double[]) ->
let currentPrices : double[] = ret.Item1
let previousPrices: double[] = ret.Item2
let currentWeights: double[] = ws
// imperative for loop to walk over three arrays
// and calculate returns and sumproduct with weight
// we need a single value and could get it in many
// ways without copying the arrays
)
In the last ZipN lambda we have three arrays of current and previous prices and current weights. We could calculate weighted return with them and return a single value. For each key, these arrays are refilled with new values and the last lambda is reapplied to updated arrays.
When all series are continuous, we get full outer join and the resulting series will have a union of all keys from input series, with values defined by continuous series constructor. Other than repeat/fill it could be linear or spline interpolation, a forecast from moving regression or any other complex logic that is hidden inside an input continuous series. For outside world, such a continuous series becomes defined at every point, inner join assumes that every key exists and zipping works as expected just as if we had precalculated every point. But this works without allocating memory and also works in real-time for streaming data.
PM> Install-Package Spreads
PRs & issues are welcome!
This Source Code Form is subject to the terms of the Mozilla Public License, v. 2.0. If a copy of the MPL was not distributed with this file, You can obtain one at http://mozilla.org/MPL/2.0/.
(c) Victor Baybekov, 2014-2017
Current status is alpha and we are actively working on 1.0-beta release. We will use semantic versioning after 1.0 release.
- Twitter @DataSpreads
- Introducing Spreads library about why and how Spreads library was born.
- How to write the simplest trading strategy using Spreads.
- Technical introduction with pictures: updated slides from Feb'16 London F# Meetup.