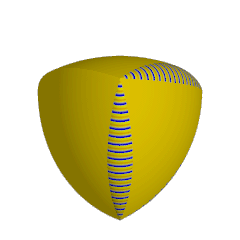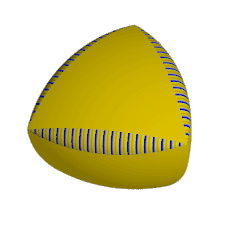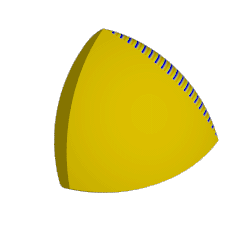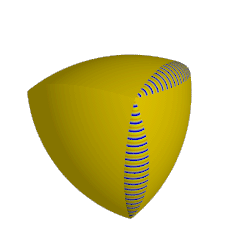
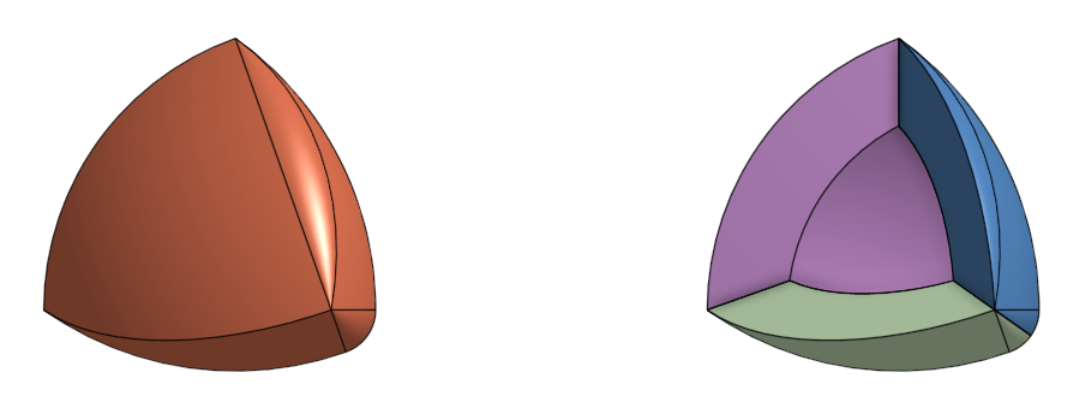3D models of both, the Reuleaux tetrahedron and Meissner body in STEP and STL formats that can be used in 3D dedign or printing.
But why this is interesting?
The Reuleaux tetrahedron and the Meissner tetrahedra are both three-dimensional shapes that are related to the Reuleaux triangle, a two-dimensional curve of constant width.
When rotated, a disk will keep its centre fixed, while the Reuleaux triangel will have its centre of gravity rotating on a circular path.
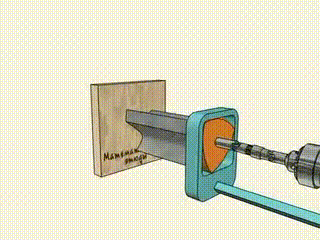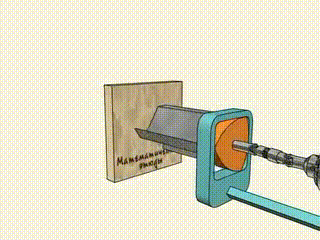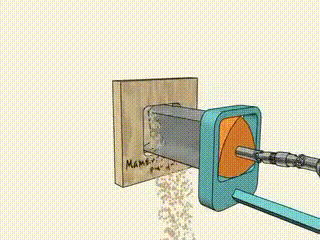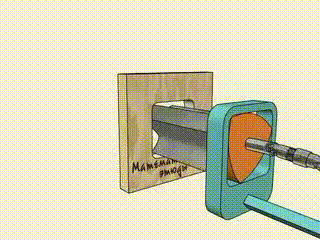
This is an interesting property that is used to for example to drill square holes:
The Reuleaux tetrahedron is the intersection of four balls centered at the vertices of a regular tetrahedron. It has the same face structure as a regular tetrahedron, but with curved faces: four vertices, and four curved faces, connected by six circular-arc edges.
Because the Reuleaux tetrahedron is not a surface of a constant width like the triangle Releaux on a 2D surface, Ernst Meissner and Friedrich Schilling showed how to modify the Reuleaux tetrahedron to form a surface of constant width, by replacing three of its edge arcs by curved patches formed as the surfaces of rotation of a circular arc. It is conjectured that the Meissner tetrahedra have the smallest volume among all solids of constant width, but this has not been mathematically demonstrated (yet 😉).
- Reuleaux tetrahedron & Meissner tetrahedra
- Sides of both to create a hollowed shape and assemble it, magnets can be used for assembly
Happy 3D printing!
Reuleaux Triangle shape has been used a lot in Ghotic architecture
and nowadays used in... pencils