Skip to content

linked list #24

New issue

Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.

Sign up for GitHub

By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.

Already on GitHub? Sign in to your account

Merged
merged 14 commits into from
Aug 1, 2023
Merged

linked list #24

Show file tree
Hide file tree
Changes from all commits
Commits
Show all changes
14 commits
Select commit Hold shift + click to select a range
d307367
docs: readme for linkedlist
yeoshuheng Jul 29, 2023
2abbf00
docs: fixed readme typo
yeoshuheng Jul 29, 2023
5607eef
docs: fix skiplist section
yeoshuheng Jul 29, 2023
fff8d01
feat: added notes, changed jdocs, reordered funcs
yeoshuheng Jul 29, 2023
a34bce5
docs: reformat png
yeoshuheng Jul 29, 2023
d884d59
refactor: remove dir
yeoshuheng Jul 29, 2023
69432d4
feat: junit test for ll
yeoshuheng Jul 29, 2023
41bc522
fix: error in test
yeoshuheng Jul 29, 2023
7379cae
refactor: shifted to legacy
yeoshuheng Jul 29, 2023
5e58a95
docs: update README.md
yeoshuheng Jul 29, 2023
784e270
docs: update README.md
yeoshuheng Jul 29, 2023
df8e80e
docs: edited javadocs based on review
yeoshuheng Aug 1, 2023
90eb119
docs: remove search, insert ops
yeoshuheng Aug 1, 2023
a73908f
docs: added dbl linkedlist + refactored layout
yeoshuheng Aug 1, 2023
File filter

Filter by extension

Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
134 changes: 72 additions & 62 deletions src/dataStructures/linkedList/LinkedList.java
View file
Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -40,7 +40,7 @@ public LinkedList(Node<T> head) {
this.head = head;
Node<T> trav = head;
int count = 0;
while (trav != null) {
while (trav != null) { // We count the size of our linked list through iteration.
count++;
trav = trav.next;
}
Expand All @@ -60,24 +60,6 @@ public int size() {
return this.size;
}

/**
* Inserts the object at the front of the linked list
* @param object to be inserted
* @return boolean representing whether insertion was successful
*/
public boolean insertFront(T object) {
return insert(object, 0);
}

/**
* Inserts the object at the end of the linked list
* @param object to be inserted
* @return boolean representing whether insertion was successful
*/
public boolean insertEnd(T object) {
return insert(object, this.size);
}

/**
* inserts the object at the specified index of the linked list
* @param object to be inserted
Expand All @@ -92,7 +74,7 @@ public boolean insert(T object, int idx) {

Node<T> newNode = new Node<>(object);

if (head == null) {
if (head == null) { // Linked list empty; We just need to add the head;
head = newNode;
size++;
return true;
Expand All @@ -105,7 +87,7 @@ public boolean insert(T object, int idx) {
trav = trav.next;
}

if (prev != null) {
if (prev != null) { // Reset the pointer at the index.
prev.next = newNode;
newNode.next = trav;
} else { // case when inserting at index 0; need to update head
Expand All @@ -116,6 +98,24 @@ public boolean insert(T object, int idx) {
return true;
}

/**
* Inserts the object at the front of the linked list
* @param object to be inserted
* @return boolean representing whether insertion was successful
*/
public boolean insertFront(T object) {
return insert(object, 0);
}

/**
* Inserts the object at the end of the linked list
* @param object to be inserted
* @return boolean representing whether insertion was successful
*/
public boolean insertEnd(T object) {
return insert(object, this.size);
}

/**
* remove the node at the specified index
* @param idx of the node to be removed
Expand All @@ -133,7 +133,7 @@ public T remove(int idx) {
for (int i = 0; i < idx; i++) {
prev = trav;
trav = trav.next;
}
} // This iteration allows us to store a copy of nodes before and after idx.

if (prev != null) {
prev.next = trav.next;
Expand All @@ -144,15 +144,38 @@ public T remove(int idx) {
return trav.val;
}

/**
* search for the 1st encounter of the node that holds the specified object
* @param object
* @return index of the node found
*/
public int search(T object) {
Node<T> trav = head;
int idx = 0;
if (trav == null) { // Empty linked list.
return -1;
}

while (trav != null) {
if (trav.val.equals(object)) {
return idx;
}
idx++;
trav = trav.next;
}

return -1;
}

/**
* delete the 1st encounter of the specified object from the linked list
* @param object to search and delete
* @return boolean whether the delete op was successful
*/
public boolean delete(T object) {
int idx = search(object);
int idx = search(object); // Get index of object to remove.
if (idx != -1) {
remove(idx);
remove(idx); // Remove based on that index.
return true;
}
return false;
Expand All @@ -174,28 +197,6 @@ public T poll() {
return remove(0);
}

/**
* search for the 1st encounter of the node that holds the specified object
* @param object
* @return index of the node found
*/
public int search(T object) {
Node<T> trav = head;
int idx = 0;
if (trav == null) {
return -1;
}

while (trav != null) {
if (trav.val.equals(object)) {
return idx;
}
idx++;
trav = trav.next;
}

return -1;
}

/**
* get the node at the specified index
Expand All @@ -204,7 +205,7 @@ public int search(T object) {
*/
public Node<T> get(int idx) {
Node<T> trav = head;
if (idx < this.size && trav != null) {
if (idx < this.size && trav != null) { // Check: idx is valid & linked list not empty.
for (int i = 0; i < idx; i++) {
trav = trav.next;
}
Expand All @@ -214,29 +215,38 @@ public Node<T> get(int idx) {
}

/**
* reverse the linked list
* reverse the linked list.
* A good video to visualise this algorithm can be found
* <a = https://www.youtube.com/watch?v=D7y_hoT_YZI, href = "url">here</a>.
*/
public void reverse() {
if (head == null || head.next == null) {
if (head == null || head.next == null) { // No need to reverse if list is empty or only 1 element.
return;
}

Node<T> prev = head;
Node<T> curr = head.next;
Node<T> newHead = curr;
prev.next = null;
Node<T> newHead = curr; // Store the next head.
prev.next = null; // Reset to null, representing end of list.
while (curr.next != null) {
newHead = curr.next;
curr.next = prev;
newHead = curr.next; // We set the next element as the newHead.
curr.next = prev; // Replace our current node as the previous node.
prev = curr;
curr = newHead;
curr = newHead; // Set our current node as the next element (newHead) to look at.
}
newHead.next = prev;
head = newHead;
head = newHead; // newHead is last ele from org. list -> First ele of our reversed list.
}

/**
* sorts the linked list by their natural order
* Sorts the linked list by the natural order of the elements.
* Generally, merge sort is the most efficient sorting algorithm for linked lists.
* Addressing a random node in the linked list incurrs O(n) time complexity.
* This makes sort algorithms like quicksort and heapsort inefficient since they rely
* on the O(1) lookup time of an array.
*
* A good video to visualise this algorithm can be found
* <a = https://www.youtube.com/watch?v=JSceec-wEyw, href = "url">here</a>.
*/
public void sort() {
if (this.size <= 1) {
Expand All @@ -245,11 +255,11 @@ public void sort() {
int mid = (this.size - 1) / 2;
Node<T> middle = this.get(mid);
Node<T> nextHead = middle.next;
LinkedList<T> next = new LinkedList<>(nextHead, this.size - 1 - mid);
LinkedList<T> next = new LinkedList<>(nextHead, this.size - 1 - mid); // Split the list into 2.
middle.next = null;
this.size = mid + 1; // update size of original LL after split
this.size = mid + 1; // update size of original list after split

next.sort();
next.sort(); // Recursively sort the list.
this.sort();
head = merge(this, next);
}
Expand All @@ -268,6 +278,7 @@ private Node<T> merge(LinkedList<T> first, LinkedList<T> second) {

while (headFirst != null && headSecond != null) {
if (headFirst.val.compareTo(headSecond.val) < 0) {
// Note that first & second either only have 2 values or are already sorted.
trav.next = headFirst;
headFirst = headFirst.next;
} else {
Expand All @@ -277,10 +288,9 @@ private Node<T> merge(LinkedList<T> first, LinkedList<T> second) {
trav = trav.next;
}

if (headFirst != null) {
if (headFirst != null) { // Add any remaining nodes from first.
trav.next = headFirst;
}
if (headSecond != null) {
} else { // We know loop terminated because of second; Add any remaining nodes from second.
trav.next = headSecond;
}
return dummy.next;
Expand Down
84 changes: 84 additions & 0 deletions src/dataStructures/linkedList/README.md
View file
Open in desktop
Original file line number Diff line number Diff line change
@@ -0,0 +1,84 @@
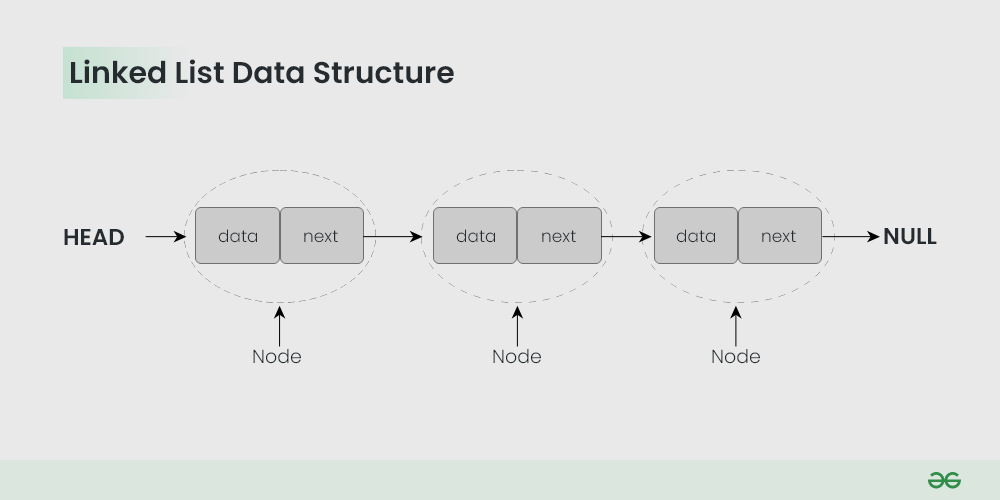
# Linked Lists
Copy link
Owner

Choose a reason for hiding this comment

The reason will be displayed to describe this comment to others. Learn more.

This is great and comprehensive! Just some restructuring as per amadeus' suggestion on standardisation.

You can follow these headers, with some room for flexibility for sub-sections within each section.

# Title
Introduction or context or commonly misunderstood stuff. Stuff to tell the reader that we know the current context and all. so yup Linked List vs Arrays is one good example.

## Analysis
Here we discuss time and space complexity of the whole algorithm. Perhaps if the algorithm has a non-trivial sub-routine, and its worth discussing more, than you can discuss how the analysis is derived here. No need to discuss implementation-specific unless necessary (though in-line comment in the code itself might better help), grab the general idea and present.

## Notes / Further Details / Conclusion
Here is an optional section to discuss further misc details that do not fit above but you believe to be crucial for students to be aware of. I think your addition of variants is one good example! You discussion on memory requirements, with linked list being a versatile structure that does not require a fixed size to be declared can put here too.

I noticed you discussed search and insert operations. I think these are not necessary and we probably should avoid making it a standard else its more workload. Only operations that are non-trivial (not easily inferred from code) should then be considered for discussion here. For linked list, i think its fine to omit since most students should be able to easily parse the logic from the code.

One last thing, for each of the ## sections, you can do what you did of segregating further into ### sub-sections if you wish.

Linked lists are a linear structure used to store data elements.
It consists of a collection of objects, used to store our data elements, known as nodes.

![Linked list image](https://media.geeksforgeeks.org/wp-content/cdn-uploads/20230726162542/Linked-List-Data-Structure.png)

*Source: GeeksForGeeks*

### Linked Lists vs Arrays
Linked lists are similar to arrays in
terms of used and purpose, but there are considerations when deciding which structure to use.

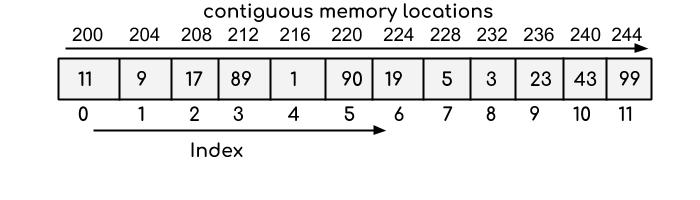
Unlike arrays, which are stored in contiguous locations in memory,
linked lists are stored across memory and are connected to each other via pointers.

![Array image](https://beginnersbook.com/wp-content/uploads/2018/10/array.jpg)

*Source: BeginnersBook*

## Analysis
Some common operations involved in a linked list includes looking up elements in a linked list and inserting elements into a linked list.

Searching a linked list requires O(n) time complexity whereas inserting into a linked list from a specified index requires O(n) time complexity.

## Notes / Further Details / Conclusion

### Memory Requirements & Flexibility
As a contiguous block of memory must be allocated for an array, its size is fixed.
If we declare a array of size *n*, but only allocate *x* elements, where *x < n*,
we will be left with unused, wasted memory.

This waste does not occur with linked lists, which only take up memory as new elements are added.
However, additional space will be used to store the pointers.

As the declared size of our array is static (done at compile time), we are also given less flexibility if
we end up needing to store more elements at run time.

However, linked list gives us the option of adding new nodes at run time based on our requirements,
allowing us to allocate memory to store items dynamically, giving us more flexibility.

### Conclusion
You should aim to use linked list in scenarios where you cannot predict how many elements you need to store
or if you require constant time insertions to the list.

However, arrays would be preferred if you already know the amount of elements you need to store ahead of time.
It would also be preferred if you are conducting a lot of look up operations.

## Linked List Variants
Copy link
Owner

Choose a reason for hiding this comment

The reason will be displayed to describe this comment to others. Learn more.

Do mention double-linked list too. This is the most common variant after the conventional linked list, that allows popping of elements from front and back. Java's Deque (double-ended queue i believe) is essentially a double-linkedlist

The lookup time within a linked list is its biggest issue.
However, there are variants of linked lists designed to speed up lookup time.

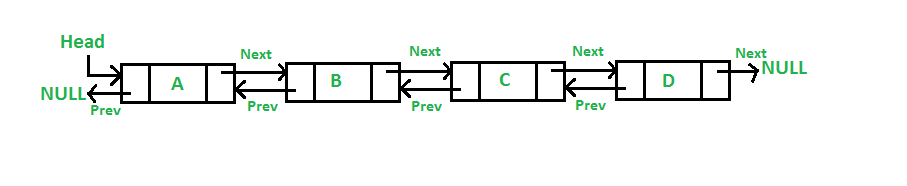
### Doubly Linked List

![Doubly Linked List](https://media.geeksforgeeks.org/wp-content/cdn-uploads/gq/2014/03/DLL1.png)

*Source: GeeksForGeeks*

This is a variant of the linked list with each node containing the pointer to not just the next note, but also the previous node.

Unlike the standard linked list, this allows us to traverse the list in the backwards direction too, this makes it a good data structure to use when implementing undo / redo functions. However, when implementing a doubly linked list, it is vital to ensure that you consider and maintain **both** pointers.

It is also worth noting that insertion from the front and back of the linked list is a O(1) operation. (Since we now only need to change the pointers in the node.)

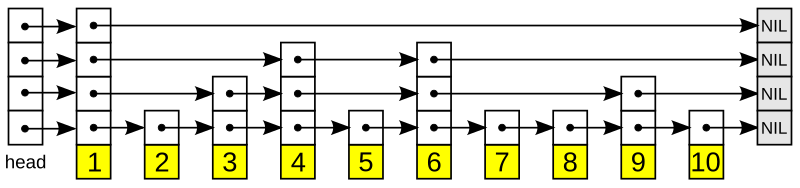
### Skip list

![Skip List](https://upload.wikimedia.org/wikipedia/commons/thumb/8/86/Skip_list.svg/800px-Skip_list.svg.png)

*Source: Brilliant*

This is a variant of a linked list with additional pointer paths that does not lead to the next node
but allow you to skip through nodes in a "express pointer path" which can be user configured.
If we know which nodes each express pointer path stops at, we would be able to conduct faster lookup.

This would also be ideal in situations where we want to store a large amount
of data which we do not need to access regularly that we are not willing to delete.

### Unrolled Linked Lists

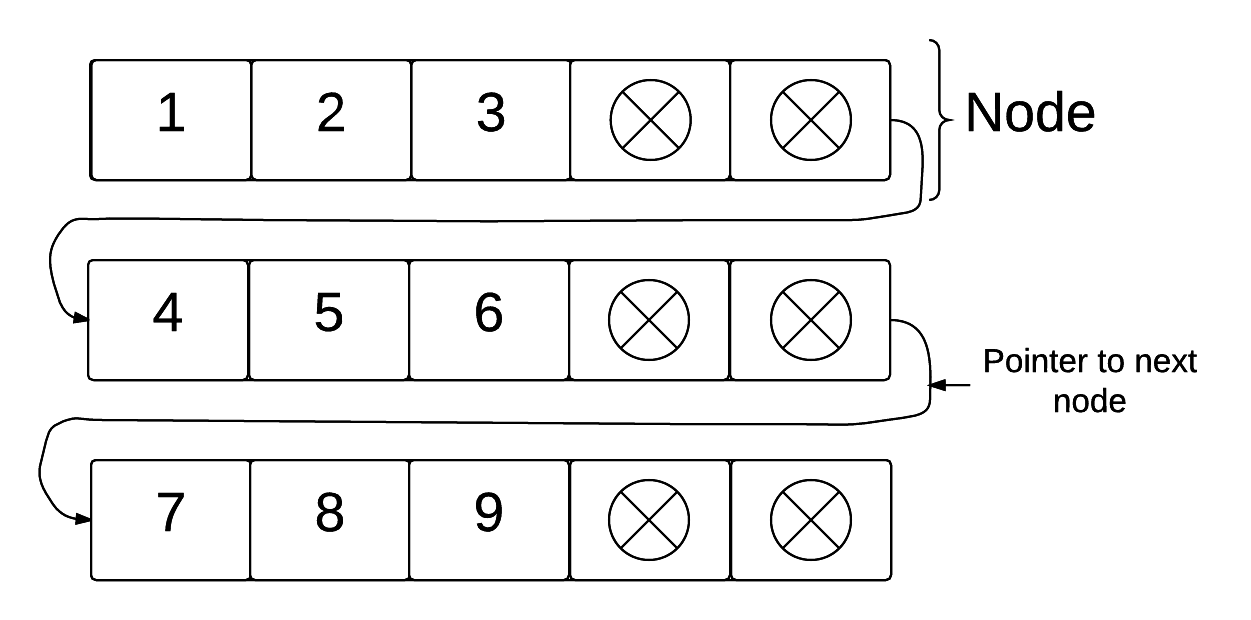![Unrolled Linked List](https://ds055uzetaobb.cloudfront.net/brioche/uploads/5LFjevVjNy-ull-new-page.png?width=2400)

*Source: Brilliant*

Unrolled linked lists stores multiple consecutive elements into a single bucket node.
This allows us to avoid constantly travelling down nodes to get to the element we need.
Loading