AVL-Tree:

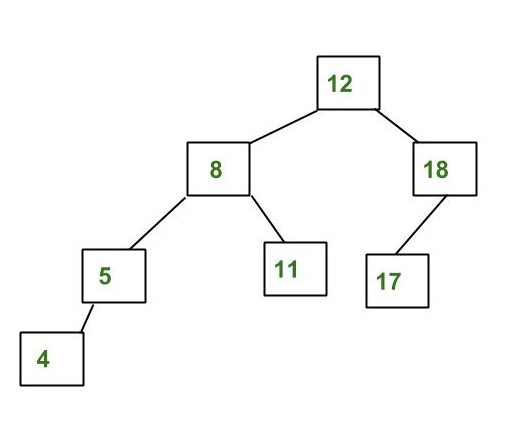
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

Example of AVL Tree:

The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.

Why AVL Trees?

Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log(n)) after every insertion and deletion, then we can guarantee an upper bound of O(log(n)) for all these operations. The height of an AVL tree is always O(log(n)) where n is the number of nodes in the tree.

Operations:

Insertion in AVL Tree - avl_insert(node* root, x, y):

The function receives a value (x, y) and inserts it into the tree. If there is already a node with key x, you will do nothing. The function returns a pointer to the root of the tree. To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).

T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side)

Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)

Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)

• Approach: The idea is to use recursive BST insert, after insertion, we get pointers to all ancestors one by one in a bottom-up manner. So we don’t need a parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the newly inserted node.

Search in AVL - avl_search():

A function that receives the root of the tree and a requested cell for search, the function searches for the node that value(x, y) and returns a pointer to it if it is found, otherwise returns NULL.

Delete in AVL - avl_delete(node* root, x, y): The function gets (x, y) and deletes the node from the tree if it exists. The function returns a pointer to the root of the tree. Approach as insertion.

Range query - avl_range_query(node* root, x, y): The function accepts two x-values and returns the largest y among all points in the field, such that: {(x, y)| x1 <= x <= x2}

• Approach:
  1. We will search the tree with value x1 and value x2.
  2. If one of them is NULL - they were not found and in particular there is no y value as required.
  3. Otherwise: search for the maximum y in the domain recursively