Repository ini merupakan arsip pengumpulan tugas saya selama satu semester pada matakuliah Praktikum Struktur Data yang dibimbing oleh dosen kami yakni Randi Proska Sandra, S.Pd, M.Sc. Tugas pada repository ini diperuntukkan mahasiswa Informatika agar memahami konsep struktur data pada pemrograman terkhusus pada pemrograman bahasa C.
| Jobsheet 1 | Jobsheet 2 | Jobsheet 3 | Jobsheet 4 |
| Jobsheet 5 | Jobsheet 6 | Jobsheet 7 | Jobsheet 8 |
| Jobsheet 9 | Jobsheet 10 | Jobsheet 11 | Jobsheet 12 |
| Jobsheet 13 |
Struktur data adalah cara untuk menyimpan, mengatur, dan mengakses data dengan efisien. Dalam praktikum ini, kita akan mempelajari struktur data sederhana seperti array dan record, serta struktur data majemuk seperti Linear (stack, queue, list, multilist) dan Non-Linier (pohon biner dan graph).
Array adalah kumpulan elemen data yang disimpan secara berurutan dalam memori komputer. Setiap elemen memiliki indeks yang memungkinkan akses langsung ke elemen tersebut.
Record adalah kumpulan data yang terdiri dari beberapa field atau atribut yang memiliki tipe data yang berbeda-beda. Setiap field dalam record dapat diakses secara terpisah.
Stack adalah struktur data LIFO (Last In, First Out) yang mendukung operasi push (menambahkan elemen) dan pop (menghapus elemen). Elemen yang terakhir dimasukkan ke dalam stack akan menjadi elemen pertama yang dihapus.
Queue adalah struktur data FIFO (First In, First Out) yang mendukung operasi enqueue (menambahkan elemen) dan dequeue (menghapus elemen). Elemen yang pertama dimasukkan ke dalam queue akan menjadi elemen pertama yang dihapus.
List adalah kumpulan elemen data yang diatur secara linier. Terdapat dua jenis list, yaitu linked list dan array list, yang memiliki cara penyimpanan dan akses data yang berbeda.
Multilist adalah struktur data yang mengorganisir elemen data dalam bentuk graf terarah dengan beberapa jenis edge atau sisi.
Binary Tree adalah struktur data hierarkis yang terdiri dari simpul-simpul (nodes) yang memiliki dua anak, yaitu anak kiri dan anak kanan.
Graph adalah struktur data yang terdiri dari kumpulan simpul (nodes) yang terhubung oleh edge atau sisi. Graph dapat digunakan untuk merepresentasikan hubungan antar objek.
Struktur data adalah cara untuk menyimpan, mengatur, dan mengakses data dengan efisien. Dalam praktikum ini, kita akan mempelajari struktur data sederhana seperti array dan record, serta struktur data majemuk seperti Linear (stack, queue, list, multilist) dan Non-Linier (pohon biner dan graph).
Array adalah struktur data yang terdiri dari kumpulan elemen dengan tipe data yang sama yang disimpan secara berurutan dalam memori komputer. Setiap elemen dalam array dapat diakses menggunakan indeksnya. Contoh penggunaan array dalam C:
int numbers[5] = {1, 2, 3, 4, 5}; // Mendefinisikan array numbers dengan 5 elemen
int x = numbers[2]; // Mengakses elemen ke-3 dari array numbersPointer adalah variabel yang menyimpan alamat memori dari variabel lain. Dengan menggunakan pointer, kita dapat mengakses dan memanipulasi nilai variabel secara langsung di dalam memori. Contoh penggunaan pointer dalam C:
int a = 10;
int *ptr; // Mendefinisikan pointer ptr
ptr = &a; // Mengisi ptr dengan alamat memori variabel a
printf("Nilai a: %d\n", *ptr); // Mengakses nilai a melalui pointer ptrStructure adalah cara untuk menggabungkan beberapa tipe data menjadi satu tipe data baru yang lebih kompleks. Struktur digunakan untuk merepresentasikan objek dengan atribut-atributnya. Contoh penggunaan structure dalam C:
struct Mahasiswa {
char nama[50];
int umur;
float ipk;
};
struct Mahasiswa mhs1; // Mendefinisikan variabel mhs1 dengan tipe data struct Mahasiswa
strcpy(mhs1.nama, "John Doe"); // Mengisi nilai atribut nama pada mhs1
mhs1.umur = 20;
mhs1.ipk = 3.75;ADT adalah konsep yang menggabungkan struktur data dengan operasi-operasi yang dapat dilakukan terhadap struktur data tersebut. ADT tidak mengikat implementasi struktur data tertentu, sehingga memungkinkan penggunaan berbagai teknik pemrograman. Contoh ADT dalam C adalah implementasi stack:
// Definisi ADT Stack
#define MAX_SIZE 100
typedef struct {
int items[MAX_SIZE];
int top;
} Stack;
// Operasi-operasi pada Stack
void push(Stack *s, int value) {
if (s->top == MAX_SIZE - 1) {
printf("Stack penuh\n");
} else {
s->top++;
s->items[s->top] = value;
}
}
int pop(Stack *s) {
if (s->top == -1) {
printf("Stack kosong\n");
return -1;
} else {
int temp = s->items[s->top];
s->top--;
return temp;
}
}Linked list adalah struktur data linier yang terdiri dari sekelompok node yang terhubung satu sama lain melalui pointer. Setiap node memiliki dua bagian, yaitu data atau nilai yang disimpan dan pointer yang menunjukkan ke node berikutnya dalam linked list.
Linked list dapat dibagi menjadi dua jenis utama:
- Singly Linked List: Setiap node memiliki satu pointer yang menunjuk ke node berikutnya.
- Doubly Linked List: Setiap node memiliki dua pointer, yaitu pointer yang menunjuk ke node sebelumnya dan pointer yang menunjuk ke node berikutnya.
- Setiap node dalam linked list terdiri dari dua bagian utama: data (nilai yang disimpan) dan pointer (alamat memori node berikutnya).
- Node pertama disebut sebagai head yang menunjuk ke node pertama dalam linked list.
- Node terakhir memiliki pointer bernilai NULL untuk menandakan akhir dari linked list.
Berikut adalah contoh implementasi singly linked list sederhana dalam bahasa C:
#include <stdio.h>
#include <stdlib.h>
// Struktur Node
struct Node {
int data;
struct Node* next;
};
// Fungsi untuk menambahkan node baru di awal linked list
void insertAtBeginning(struct Node** head_ref, int new_data) {
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = *head_ref;
*head_ref = new_node;
}
// Fungsi untuk mencetak linked list
void printList(struct Node* node) {
while (node != NULL) {
printf("%d -> ", node->data);
node = node->next;
}
printf("NULL\n");
}
int main() {
struct Node* head = NULL;
// Menambahkan node-node baru di awal linked list
insertAtBeginning(&head, 3);
insertAtBeginning(&head, 5);
insertAtBeginning(&head, 7);
// Mencetak linked list
printf("Linked List: ");
printList(head);
return 0;
}Dalam contoh di atas, kita menggunakan struktur Node untuk merepresentasikan node dalam linked list. Fungsi insertAtBeginning digunakan untuk menambahkan node baru di awal linked list, dan fungsi printList digunakan untuk mencetak isi linked list.
Doubly linked list adalah struktur data linier yang mirip dengan singly linked list, tetapi setiap node dalam doubly linked list memiliki dua pointer: satu untuk menunjuk ke node sebelumnya (prev) dan satu untuk menunjuk ke node berikutnya (next). Hal ini memungkinkan navigasi maju dan mundur dalam linked list.
Setiap node dalam doubly linked list terdiri dari tiga bagian utama:
- Data: Menyimpan nilai atau informasi yang diinginkan.
- Pointer prev: Menunjuk ke node sebelumnya dalam linked list.
- Pointer next: Menunjuk ke node berikutnya dalam linked list.
- Setiap node memiliki dua pointer, yaitu pointer prev dan pointer next.
- Node pertama disebut sebagai head yang menunjuk ke node pertama dalam linked list.
- Node terakhir disebut sebagai tail yang menunjuk ke NULL pada pointer next-nya.
Berikut adalah contoh implementasi doubly linked list dalam bahasa C:
#include <stdio.h>
#include <stdlib.h>
// Struktur Node
struct Node {
int data;
struct Node* prev;
struct Node* next;
};
// Fungsi untuk menambahkan node baru di awal linked list
void insertAtBeginning(struct Node** head_ref, int new_data) {
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->prev = NULL;
new_node->next = *head_ref;
if (*head_ref != NULL) {
(*head_ref)->prev = new_node;
}
*head_ref = new_node;
}
// Fungsi untuk mencetak linked list dari depan
void printForward(struct Node* node) {
while (node != NULL) {
printf("%d -> ", node->data);
node = node->next;
}
printf("NULL\n");
}
// Fungsi untuk mencetak linked list dari belakang
void printBackward(struct Node* node) {
while (node->next != NULL) {
node = node->next;
}
while (node != NULL) {
printf("%d -> ", node->data);
node = node->prev;
}
printf("NULL\n");
}
int main() {
struct Node* head = NULL;
// Menambahkan node-node baru di awal linked list
insertAtBeginning(&head, 3);
insertAtBeginning(&head, 5);
insertAtBeginning(&head, 7);
// Mencetak linked list dari depan
printf("Linked List (Forward): ");
printForward(head);
// Mencetak linked list dari belakang
printf("Linked List (Backward): ");
printBackward(head);
return 0;
}Dalam contoh di atas, kita menggunakan struktur Node dengan pointer prev dan next untuk merepresentasikan node dalam doubly linked list. Fungsi insertAtBeginning digunakan untuk menambahkan node baru di awal linked list, dan fungsi printForward dan printBackward digunakan untuk mencetak isi linked list dari depan dan belakang.
Circular linked list dan circular doubly linked list adalah struktur data linier yang memiliki karakteristik khusus di mana node terakhir menunjuk kembali ke node pertama, membentuk lingkaran atau sirkuit. Circular doubly linked list mirip dengan circular linked list, tetapi setiap node dalam circular doubly linked list memiliki dua pointer: satu untuk menunjuk ke node sebelumnya (prev) dan satu untuk menunjuk ke node berikutnya (next).
Circular linked list adalah struktur data linier di mana setiap node memiliki pointer yang menunjuk ke node berikutnya, dan node terakhir menunjuk kembali ke node pertama, membentuk lingkaran.
- Setiap node memiliki satu pointer yang menunjuk ke node berikutnya.
- Node terakhir (tail) menunjuk kembali ke node pertama (head), membentuk lingkaran.
Berikut adalah contoh implementasi circular linked list dalam bahasa C:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
// Fungsi-fungsi lainnya (seperti insert, delete, dll.) dapat ditambahkan sesuai kebutuhanCircular doubly linked list adalah struktur data linier di mana setiap node memiliki dua pointer: satu untuk menunjuk ke node sebelumnya (prev) dan satu untuk menunjuk ke node berikutnya (next). Node terakhir (tail) menunjuk kembali ke node pertama (head), membentuk lingkaran.
Setiap node memiliki dua pointer, yaitu pointer prev dan pointer next. Node pertama disebut sebagai head yang menunjuk ke node pertama dalam linked list. Node terakhir disebut sebagai tail yang menunjuk kembali ke node pertama.
Berikut adalah contoh implementasi circular doubly linked list dalam bahasa C:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* prev;
struct Node* next;
};
// Fungsi-fungsi lainnya (seperti insert, delete, dll.) dapat ditambahkan sesuai kebutuhan- Circular linked list: Setiap node memiliki satu pointer (next).
- Circular doubly linked list: Setiap node memiliki dua pointer (prev dan next).
- Circular linked list memungkinkan navigasi maju tanpa batas, karena node terakhir menunjuk kembali ke node pertama.
- Circular doubly linked list memungkinkan navigasi maju dan mundur (dari depan ke belakang dan sebaliknya).
- Circular linked list dapat lebih efisien dalam penggunaan memori karena hanya memiliki satu pointer per node.
- Circular doubly linked list membutuhkan lebih banyak ruang memori karena setiap node memiliki dua pointer.
Stack adalah struktur data linier yang mengikuti prinsip LIFO (Last In, First Out), artinya elemen terakhir yang dimasukkan ke dalam stack akan menjadi elemen pertama yang keluar. Operasi pada stack meliputi push (menambahkan elemen ke stack) dan pop (menghapus elemen dari stack).
Stack terdiri dari tiga operasi utama:
- Push: Menambahkan elemen ke dalam stack.
- Pop: Menghapus elemen teratas dari stack.
- Peek: Melihat nilai elemen teratas dari stack tanpa menghapusnya.
- Setiap node dalam stack memiliki dua bagian utama: data (nilai yang disimpan) dan pointer (alamat memori node sebelumnya).
- Elemen terbaru ditambahkan ke atas stack.
- Elemen teratas (top) adalah elemen yang paling baru ditambahkan dan yang akan dihapus saat operasi pop dilakukan.
Berikut adalah contoh implementasi stack menggunakan array dalam bahasa C:
#include <stdio.h>
#define MAX_SIZE 100 // Ukuran maksimum stack
// Struktur Stack
struct Stack {
int items[MAX_SIZE];
int top;
};
// Inisialisasi stack
void initStack(struct Stack* stack) {
stack->top = -1;
}
// Fungsi untuk mengecek apakah stack kosong
int isEmpty(struct Stack* stack) {
return stack->top == -1;
}
// Fungsi untuk mengecek apakah stack penuh
int isFull(struct Stack* stack) {
return stack->top == MAX_SIZE - 1;
}
// Fungsi untuk menambahkan elemen ke dalam stack (push)
void push(struct Stack* stack, int item) {
if (isFull(stack)) {
printf("Stack Overflow\n");
return;
}
stack->items[++stack->top] = item;
}
// Fungsi untuk menghapus elemen teratas dari stack (pop)
int pop(struct Stack* stack) {
if (isEmpty(stack)) {
printf("Stack Underflow\n");
return -1;
}
return stack->items[stack->top--];
}
// Fungsi untuk melihat elemen teratas dari stack (peek)
int peek(struct Stack* stack) {
if (isEmpty(stack)) {
printf("Stack is empty\n");
return -1;
}
return stack->items[stack->top];
}
int main() {
struct Stack stack;
initStack(&stack);
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Elemen teratas: %d\n", peek(&stack));
printf("Elemen yang dihapus: %d\n", pop(&stack));
printf("Elemen teratas setelah pop: %d\n", peek(&stack));
return 0;
}Dalam contoh di atas, kita menggunakan array untuk menyimpan elemen-elemen stack. Fungsi-fungsi seperti push, pop, peek, isEmpty, dan isFull digunakan untuk operasi-operasi dasar pada stack.
Queue adalah struktur data linier yang mengikuti prinsip FIFO (First In, First Out), artinya elemen pertama yang dimasukkan ke dalam queue akan menjadi elemen pertama yang keluar. Operasi pada queue meliputi enqueue (menambahkan elemen ke queue) dan dequeue (menghapus elemen dari queue).
Queue terdiri dari dua operasi utama:
- Enqueue: Menambahkan elemen ke dalam queue.
- Dequeue: Menghapus elemen dari depan queue.
- Setiap node dalam queue memiliki dua bagian utama: data (nilai yang disimpan) dan pointer (alamat memori node berikutnya).
- Elemen baru ditambahkan ke belakang queue.
- Elemen di depan queue adalah elemen yang paling lama ditambahkan dan yang akan dihapus saat operasi dequeue dilakukan.
Berikut adalah contoh implementasi queue menggunakan array dalam bahasa C:
#include <stdio.h>
#define MAX_SIZE 100 // Ukuran maksimum queue
// Struktur Queue
struct Queue {
int items[MAX_SIZE];
int front;
int rear;
};
// Inisialisasi queue
void initQueue(struct Queue* queue) {
queue->front = -1;
queue->rear = -1;
}
// Fungsi untuk mengecek apakah queue kosong
int isEmpty(struct Queue* queue) {
return queue->front == -1;
}
// Fungsi untuk mengecek apakah queue penuh
int isFull(struct Queue* queue) {
return queue->rear == MAX_SIZE - 1;
}
// Fungsi untuk menambahkan elemen ke dalam queue (enqueue)
void enqueue(struct Queue* queue, int item) {
if (isFull(queue)) {
printf("Queue is full\n");
return;
}
if (isEmpty(queue)) {
queue->front = 0;
}
queue->rear++;
queue->items[queue->rear] = item;
}
// Fungsi untuk menghapus elemen dari depan queue (dequeue)
int dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
printf("Queue is empty\n");
return -1;
}
int item = queue->items[queue->front];
queue->front++;
if (queue->front > queue->rear) {
queue->front = queue->rear = -1;
}
return item;
}
// Fungsi untuk melihat elemen di depan queue (peek)
int peek(struct Queue* queue) {
if (isEmpty(queue)) {
printf("Queue is empty\n");
return -1;
}
return queue->items[queue->front];
}
int main() {
struct Queue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&queue, 30);
printf("Elemen di depan queue: %d\n", peek(&queue));
printf("Elemen yang dihapus: %d\n", dequeue(&queue));
printf("Elemen di depan queue setelah dequeue: %d\n", peek(&queue));
return 0;
}Dalam contoh di atas, kita menggunakan array untuk menyimpan elemen-elemen queue. Fungsi-fungsi seperti enqueue, dequeue, peek, isEmpty, dan isFull digunakan untuk operasi-operasi dasar pada queue.
Bubble Sort adalah salah satu algoritma pengurutan sederhana yang bekerja dengan cara membandingkan dua elemen yang bersebelahan dan menukarnya jika mereka berada dalam urutan yang salah. Proses ini diulang terus menerus hingga seluruh daftar terurut.
Langkah-langkah:
- Mulai dari awal daftar.
- Bandingkan elemen pertama dengan elemen kedua.
- Jika elemen pertama lebih besar dari elemen kedua, tukar mereka.
- Pindah ke pasangan elemen berikutnya, bandingkan dan tukar jika perlu.
- Ulangi langkah 2-4 hingga mencapai akhir daftar. Ini disebut satu "pass".
- Ulangi seluruh proses untuk seluruh daftar hingga tidak ada lagi elemen yang perlu ditukar selama satu pass penuh. Pada titik ini, daftar sudah terurut.
Implementasi dalam C:
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}- Terburuk (Worst Case): O(n^2)
- Rata-rata (Average Case): O(n^2)
- Terbaik (Best Case): O(n) - ketika daftar sudah terurut
Insertion Sort adalah algoritma pengurutan yang membangun daftar terurut satu per satu dengan cara mengambil satu elemen pada satu waktu dan menempatkannya pada posisi yang benar di antara elemen-elemen yang telah terurut sebelumnya.
Langkah-langkah:
- Mulai dari elemen kedua dalam daftar (anggap elemen pertama sudah terurut).
- Bandingkan elemen ini dengan elemen sebelumnya dan geser elemen yang lebih besar satu posisi ke kanan.
- Masukkan elemen yang diambil ke dalam posisi yang benar.
- Lanjutkan ke elemen berikutnya dan ulangi proses hingga akhir daftar.
Implementasi dalam C:
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// Pindahkan elemen arr[0..i-1], yang lebih besar dari key,
// ke satu posisi di depan posisi sekarang
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}- Terburuk (Worst Case): O(n^2)
- Rata-rata (Average Case): O(n^2)
- Terbaik (Best Case): O(n) - ketika daftar sudah terurut
Keduanya mudah dipahami dan diimplementasikan.
Kedua algoritma memiliki kompleksitas waktu rata-rata dan terburuk O(n^2), tetapi Insertion Sort lebih efisien dalam praktik pada daftar kecil atau hampir terurut.
Keduanya adalah algoritma stabil, yaitu elemen dengan nilai yang sama mempertahankan urutan relatif mereka setelah pengurutan.
Kedua algoritma ini adalah in-place, yang berarti mereka tidak memerlukan ruang tambahan yang signifikan.
Insertion Sort lebih efisien daripada Bubble Sort pada daftar yang hampir terurut. Dengan demikian, meskipun kedua algoritma sederhana, Insertion Sort umumnya lebih disukai dibandingkan Bubble Sort, terutama ketika berhadapan dengan daftar yang hampir terurut.
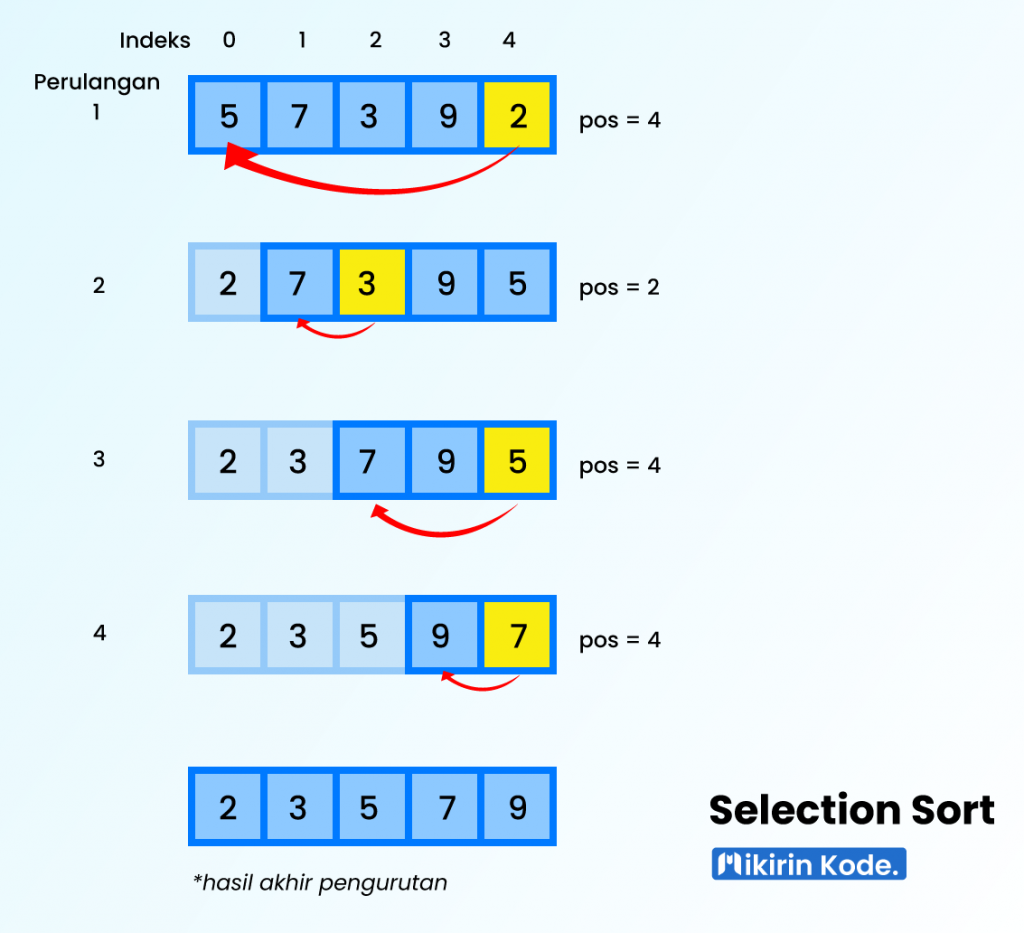
Selection Sort adalah algoritma pengurutan yang bekerja dengan cara membagi daftar menjadi dua bagian: sublist yang terurut dan sublist yang tidak terurut. Algoritma ini secara iteratif memilih elemen terkecil (atau terbesar, tergantung pada urutan yang diinginkan) dari sublist yang tidak terurut dan menempatkannya di akhir sublist yang terurut.
Langkah-langkah:
- Mulai dari elemen pertama, anggap elemen ini sebagai elemen terkecil.
- Bandingkan elemen ini dengan elemen berikutnya di daftar untuk menemukan elemen terkecil di antara mereka.
- Setelah menemukan elemen terkecil, tukar elemen tersebut dengan elemen pertama.
- Ulangi proses untuk elemen berikutnya di sublist yang tidak terurut.
- Lanjutkan proses hingga seluruh daftar terurut.
Implementasi dalam C:
void selectionSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
int min_idx = i;
for (int j = i+1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// Tukar elemen terkecil yang ditemukan dengan elemen pertama dari sublist yang tidak terurut
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}- Terburuk (Worst Case): O(n^2)
- Rata-rata (Average Case): O(n^2)
- Terbaik (Best Case): O(n^2)
- Tidak tergantung pada urutan awal daftar
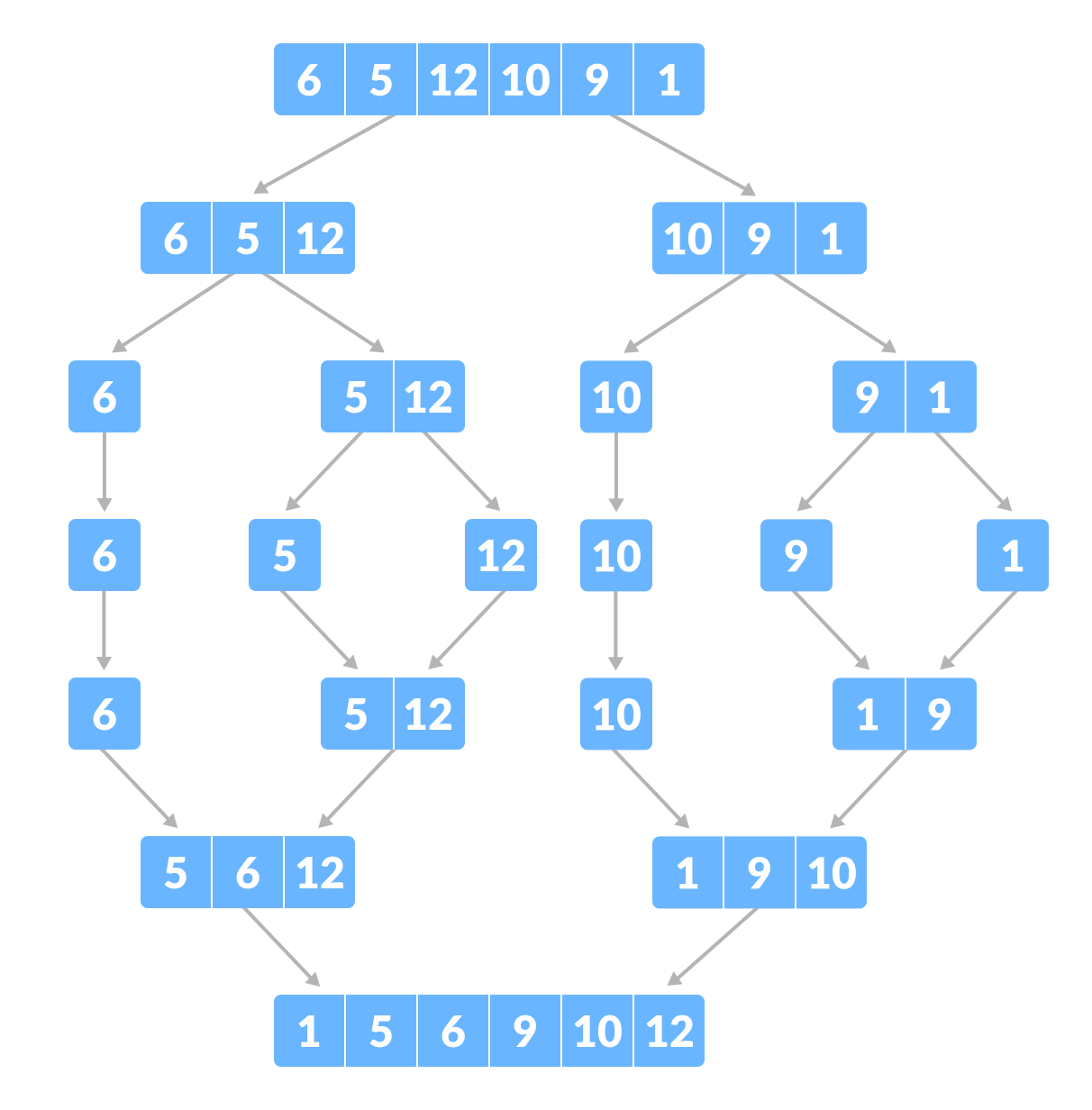
Merge Sort adalah algoritma pengurutan yang menggunakan pendekatan divide and conquer. Algoritma ini membagi daftar menjadi dua sublist yang lebih kecil, mengurutkan setiap sublist secara rekursif, dan kemudian menggabungkan dua sublist yang terurut untuk menghasilkan daftar yang terurut.
Langkah-langkah:
- Jika daftar berisi satu elemen atau kosong, maka daftar sudah terurut.
- Bagi daftar menjadi dua sublist yang lebih kecil.
- Urutkan setiap sublist secara rekursif dengan menggunakan Merge Sort.
- Gabungkan dua sublist yang terurut menjadi satu daftar terurut.
Implementasi dalam C:
void merge(int arr[], int l, int m, int r) {
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}- Terburuk (Worst Case): O(n log n)
- Rata-rata (Average Case): O(n log n)
- Terbaik (Best Case): O(n log n)
- Konsisten terlepas dari urutan awal daftar
Selection Sort mudah dipahami dan diimplementasikan tetapi tidak efisien untuk daftar besar. Merge Sort lebih kompleks tetapi sangat efisien.
- Selection Sort memiliki kompleksitas O(n^2) di semua kasus.
- Merge Sort memiliki kompleksitas O(n log n) di semua kasus.
- Selection Sort tidak stabil (elemen dengan nilai yang sama mungkin tidak mempertahankan urutan relatifnya).
- Merge Sort stabil.
Penggunaan Memori:
- Selection Sort adalah in-place, tidak memerlukan memori tambahan yang signifikan.
- Merge Sort bukan in-place, memerlukan memori tambahan untuk sublist sementara.
- Merge Sort lebih efisien untuk daftar besar dan memiliki kinerja yang konsisten.
- Selection Sort lebih cocok untuk daftar kecil atau kasus di mana kesederhanaan lebih penting daripada efisiensi.
Dengan demikian, Merge Sort lebih disukai untuk pengurutan yang efisien, terutama untuk daftar besar, sementara Selection Sort mungkin digunakan dalam konteks di mana algoritma yang lebih sederhana lebih diinginkan.
Shell Sort adalah versi yang lebih baik dari Insertion Sort. Ini bekerja dengan cara membandingkan elemen yang dipisahkan oleh interval tertentu (gap) dan mengurutkannya. Interval (gap) ini secara bertahap dikurangi hingga gap menjadi 1, di mana algoritma berubah menjadi Insertion Sort. Ini membantu dalam mengurangi jumlah pergeseran yang diperlukan oleh Insertion Sort dengan memindahkan elemen ke posisi yang lebih dekat ke tempat tujuan mereka lebih awal dalam algoritma.
Langkah-langkah:
- Pilih gap awal yang besar, kemudian bagi daftar menjadi sublist yang terdiri dari elemen yang dipisahkan oleh gap tersebut.
- Urutkan setiap sublist menggunakan Insertion Sort.
- Kurangi gap dan ulangi proses sampai gap menjadi 1.
- Pada gap 1, urutkan seluruh daftar menggunakan Insertion Sort.
Implementasi dalam C:
void shellSort(int arr[], int n) {
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = gap; i < n; i++) {
int temp = arr[i];
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = temp;
}
}
}- Terburuk (Worst Case): Bervariasi, sekitar O(n^2) untuk gap tertentu tetapi bisa lebih baik dengan gap yang lebih optimal.
- Rata-rata (Average Case): Bervariasi, biasanya sekitar O(n^1.5) hingga O(n^1.25).
- Terbaik (Best Case): O(n log n) dengan gap yang optimal.
- Tidak stabil.
Quick Sort adalah algoritma pengurutan yang menggunakan pendekatan divide and conquer. Algoritma ini memilih elemen sebagai pivot dan membagi daftar menjadi dua sublist: satu dengan elemen yang lebih kecil dari pivot dan satu lagi dengan elemen yang lebih besar dari pivot. Algoritma kemudian secara rekursif mengurutkan sublist tersebut.
Langkah-langkah:
- Pilih elemen pivot dari daftar.
- Pisahkan daftar ke dalam dua sublist: elemen yang lebih kecil dari pivot dan elemen yang lebih besar dari pivot.
- Rekursif urutkan kedua sublist.
- Gabungkan sublist yang terurut dan pivot menjadi satu daftar terurut.
Implementasi dalam C:
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}- Terburuk (Worst Case): O(n^2) terjadi ketika pivot yang dipilih adalah elemen terkecil atau terbesar setiap saat.
- Rata-rata (Average Case): O(n log n).
- Terbaik (Best Case): O(n log n).
- Tidak stabil.
- Perbandingan Shell Sort dan Quick Sort
- Shell Sort lebih mudah dipahami dan diimplementasikan daripada Quick Sort.
- Quick Sort membutuhkan pemahaman tentang rekursi dan partisi.
- Shell Sort memiliki kompleksitas waktu yang bervariasi dan biasanya lebih lambat dibandingkan dengan Quick Sort dalam kasus rata-rata.
- Quick Sort lebih cepat dalam kasus rata-rata dengan kompleksitas O(n log n).
- Shell Sort tidak stabil.
- Quick Sort tidak stabil.
- Shell Sort adalah in-place, tidak memerlukan memori tambahan yang signifikan.
- Quick Sort juga in-place, tetapi memerlukan memori tambahan untuk panggilan rekursif pada stack.
- Quick Sort lebih efisien untuk daftar besar dengan distribusi elemen yang acak.
- Shell Sort lebih cocok untuk daftar kecil atau daftar yang sebagian besar sudah terurut.
Shell Sort berguna ketika Anda memerlukan algoritma pengurutan yang sederhana dengan kinerja yang lebih baik daripada Insertion Sort, sedangkan Quick Sort adalah pilihan yang lebih baik untuk pengurutan cepat pada daftar besar dan tidak terurut.
Linear Search adalah metode pencarian sederhana yang digunakan untuk menemukan elemen dalam suatu daftar atau array. Algoritma ini bekerja dengan memeriksa setiap elemen dalam daftar satu per satu, mulai dari elemen pertama hingga elemen terakhir, sampai elemen yang dicari ditemukan atau seluruh daftar telah diperiksa.
Langkah-langkah:
- Mulai dari elemen pertama dalam daftar.
- Bandingkan elemen saat ini dengan elemen yang dicari.
- Jika elemen yang dicari ditemukan, pencarian selesai.
- Jika elemen yang dicari tidak ditemukan, pindah ke elemen berikutnya dan ulangi langkah 2 dan 3.
- Jika seluruh daftar telah diperiksa dan elemen yang dicari tidak ditemukan, pencarian gagal.
int linearSearch(int arr[], int n, int x) {
for (int i = 0; i < n; i++) {
if (arr[i] == x) {
return i; // Elemen ditemukan, kembalikan indeks
}
}
return -1; // Elemen tidak ditemukan
}- Terburuk (Worst Case): O(n), ketika elemen yang dicari berada di posisi terakhir atau tidak ada dalam daftar.
- Rata-rata (Average Case): O(n).
- Terbaik (Best Case): O(1), ketika elemen yang dicari berada di posisi pertama.
- Keuntungan: Sangat sederhana dan tidak memerlukan daftar yang terurut.
- Kerugian: Tidak efisien untuk daftar besar.
Binary Search adalah metode pencarian yang lebih efisien dibandingkan dengan Linear Search, tetapi memerlukan daftar yang terurut. Algoritma ini bekerja dengan membagi daftar menjadi dua bagian yang lebih kecil, dan membandingkan elemen tengah daftar dengan elemen yang dicari. Jika elemen yang dicari lebih kecil dari elemen tengah, pencarian dilanjutkan di bagian kiri; jika lebih besar, pencarian dilanjutkan di bagian kanan.
Langkah-langkah:
- Mulai dengan seluruh daftar.
- Temukan elemen tengah daftar.
- Bandingkan elemen tengah dengan elemen yang dicari.
- Jika elemen yang dicari sama dengan elemen tengah, pencarian selesai.
- Jika elemen yang dicari lebih kecil dari elemen tengah, ulangi langkah 1-4 pada bagian kiri daftar.
- Jika elemen yang dicari lebih besar dari elemen tengah, ulangi langkah 1-4 pada bagian kanan daftar.
- Ulangi sampai elemen yang dicari ditemukan atau daftar tidak lagi dapat dibagi.
Implementasi dalam C:
int binarySearch(int arr[], int l, int r, int x) {
while (l <= r) {
int m = l + (r - l) / 2; // Temukan elemen tengah
// Jika elemen yang dicari berada di tengah
if (arr[m] == x) {
return m;
}
// Jika elemen yang dicari lebih kecil dari elemen tengah
if (arr[m] > x) {
r = m - 1;
}
// Jika elemen yang dicari lebih besar dari elemen tengah
else {
l = m + 1;
}
}
return -1; // Elemen tidak ditemukan
}- Terburuk (Worst Case): O(log n), karena daftar dibagi menjadi dua setiap kali.
- Rata-rata (Average Case): O(log n).
- Terbaik (Best Case): O(1), ketika elemen yang dicari berada di posisi tengah awal.
- Keuntungan: Sangat efisien untuk daftar besar yang sudah terurut.
- Kerugian: Memerlukan daftar yang terurut, sehingga mungkin memerlukan waktu tambahan untuk mengurutkan daftar sebelum pencarian.
- Linear Search sangat sederhana dan mudah diimplementasikan.
- Binary Search lebih kompleks dan memerlukan pemahaman tentang pembagian dan rekursi atau iterasi.
- Linear Search tidak efisien untuk daftar besar, dengan kompleksitas waktu O(n).
- Binary Search sangat efisien untuk daftar besar yang terurut, dengan kompleksitas waktu O(log n).
- Linear Search dapat digunakan pada daftar yang tidak terurut.
- Binary Search hanya dapat digunakan pada daftar yang terurut.
- Linear Search lebih cocok untuk daftar kecil atau pencarian sekali-sekali.
- Binary Search lebih cocok untuk daftar besar yang sering dicari.
Linear Search adalah pilihan yang lebih sederhana untuk daftar kecil atau yang tidak terurut, sementara Binary -Search adalah pilihan yang lebih efisien untuk daftar besar yang sudah terurut.
Pohon adalah struktur data hierarkis yang terdiri dari simpul (node) yang terhubung oleh tepi (edge). Setiap pohon memiliki simpul akar (root) yang menjadi titik awal, dan setiap simpul dapat memiliki anak (child) yang merupakan sub-pohon dari simpul tersebut.
- Akar (Root): Simpul paling atas dari pohon. Dalam struktur data pohon, hanya ada satu akar.
- Simpul (Node): Elemen dari pohon yang dapat memiliki anak dan satu induk (kecuali akar).
- Tepi (Edge): Hubungan antara dua simpul dalam pohon.
- Daun (Leaf): Simpul yang tidak memiliki anak, terletak di bagian bawah pohon.
- Tingkat (Level): Kedalaman simpul dalam pohon, akar berada di tingkat 0.
- Tinggi Pohon (Height of Tree): Jarak maksimum dari akar ke daun terjauh.
- Sub-pohon (Subtree): Pohon yang merupakan bagian dari pohon yang lebih besar.
- Induk (Parent): Simpul yang memiliki satu atau lebih anak.
- Anak (Child): Simpul yang merupakan hasil langsung dari induknya.
- Saudara (Sibling): Simpul-simpul yang memiliki induk yang sama.
- Pohon Biner (Binary Tree): Pohon di mana setiap simpul memiliki paling banyak dua anak, yaitu anak kiri dan anak kanan.
- Pohon Biner Pencarian (Binary Search Tree, BST): Pohon biner yang mematuhi sifat pencarian biner, yaitu nilai di simpul kiri lebih kecil dari nilai di simpul induk, dan nilai di simpul kanan lebih besar dari nilai di simpul induk.
- Pohon AVL: Pohon biner pencarian yang diatur agar tetap seimbang tinggi dengan memastikan perbedaan tinggi antara sub-pohon kiri dan kanan tidak lebih dari satu.
- Heap: Pohon biner lengkap yang memenuhi sifat heap, di mana setiap simpul induk lebih besar (max-heap) atau lebih kecil (min-heap) dari anak-anaknya.
- Pohon Merah-Hitam (Red-Black Tree): Pohon biner pencarian yang memiliki properti tambahan untuk memastikan keseimbangan tinggi, di mana setiap simpul memiliki warna merah atau hitam dan mematuhi aturan warna tertentu.
- Trie: Pohon yang digunakan untuk pencarian string, di mana setiap simpul mewakili karakter dari string.
- Penelusuran (Traversal): Proses mengunjungi setiap simpul dalam pohon.
- Pre-order Traversal: Kunjungi simpul induk terlebih dahulu, lalu sub-pohon kiri, kemudian sub-pohon kanan.
- In-order Traversal: Kunjungi sub-pohon kiri terlebih dahulu, lalu simpul induk, kemudian sub-pohon kanan.
- Post-order Traversal: Kunjungi sub-pohon kiri terlebih dahulu, lalu sub-pohon kanan, kemudian simpul induk.
- Level-order Traversal: Kunjungi simpul-simpul berdasarkan tingkatnya, mulai dari akar ke daun.
-
Penyisipan (Insertion): Menambahkan simpul baru ke pohon sesuai dengan aturan pohon yang digunakan (misalnya, BST, AVL).
-
Penghapusan (Deletion): Menghapus simpul dari pohon dan memastikan pohon tetap memenuhi aturan yang berlaku.
-
Pencarian (Search): Mencari simpul dengan nilai tertentu dalam pohon.
Implementasi Dasar Pohon Biner dalam C:
#include <stdio.h>
#include <stdlib.h>
// Definisi struktur simpul pohon biner
typedef struct Node {
int data;
struct Node *left, *right;
} Node;
// Fungsi untuk membuat simpul baru
Node* newNode(int data) {
Node* node = (Node*)malloc(sizeof(Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
// Fungsi untuk penyisipan simpul baru dalam BST
Node* insert(Node* node, int data) {
if (node == NULL) return newNode(data);
if (data < node->data) {
node->left = insert(node->left, data);
} else if (data > node->data) {
node->right = insert(node->right, data);
}
return node;
}
// Fungsi untuk penelusuran in-order
void inOrderTraversal(Node* root) {
if (root != NULL) {
inOrderTraversal(root->left);
printf("%d ", root->data);
inOrderTraversal(root->right);
}
}
int main() {
Node* root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
printf("In-order traversal of the given tree: ");
inOrderTraversal(root);
return 0;
}Pohon adalah struktur data yang sangat berguna dalam berbagai aplikasi komputasi karena sifat hierarkisnya dan kemampuan untuk menangani data secara efisien. Beberapa aplikasi umum dari pohon termasuk basis data, jaringan komputer, dan kompresi data. Pemahaman tentang pohon dan berbagai jenis serta operasinya sangat penting bagi pengembang perangkat lunak dan ilmuwan komputer.
Graf adalah struktur data yang terdiri dari simpul (nodes) dan tepi (edges) yang menghubungkan pasangan simpul. Graf digunakan untuk merepresentasikan banyak jenis hubungan dan proses di dunia nyata, seperti jaringan jalan, hubungan sosial, jaringan komputer, dan lain-lain.
- Simpul (Node/Vertex): Titik dalam graf.
- Tepi (Edge): Hubungan antara dua simpul dalam graf.
- Graf Berarah (Directed Graph/Digraph): Graf di mana tepi memiliki arah.
- Graf Tak Berarah (Undirected Graph): Graf di mana tepi tidak memiliki arah.
- Graf Berbobot (Weighted Graph): Graf di mana setiap tepi memiliki nilai bobot.
- Lintasan (Path): Urutan simpul yang terhubung oleh tepi.
- Siklus (Cycle): Lintasan yang berawal dan berakhir di simpul yang sama.
- Graf Terhubung (Connected Graph): Graf di mana ada lintasan antara setiap pasangan simpul.
- Graf Tak Terhubung (Disconnected Graph): Graf yang tidak memenuhi kondisi di atas.
- Derajat (Degree): Jumlah tepi yang terhubung dengan sebuah simpul.
Breadth First Search (BFS) adalah algoritma penelusuran graf yang dimulai dari simpul awal dan mengeksplorasi semua simpul tetangga di tingkat saat ini sebelum pindah ke simpul tingkat berikutnya. BFS menggunakan struktur data antrian (queue).
- Mulai dari simpul awal dan tandai sebagai terkunjungi.
- Masukkan simpul awal ke dalam antrian.
- Selama antrian tidak kosong:
- Ambil simpul dari antrian.
- Untuk setiap tetangga simpul tersebut, jika belum dikunjungi, tandai sebagai terkunjungi dan masukkan ke dalam antrian.
Implementasi BFS dalam C:
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
int queue[MAX], front = -1, rear = -1;
int visited[MAX] = {0};
int adjMatrix[MAX][MAX];
int n; // Jumlah simpul
void enqueue(int v) {
if (rear == MAX - 1) {
printf("Queue penuh\n");
return;
}
if (front == -1) front = 0;
queue[++rear] = v;
}
int dequeue() {
if (front == -1 || front > rear) {
printf("Queue kosong\n");
return -1;
}
return queue[front++];
}
void BFS(int startVertex) {
visited[startVertex] = 1;
enqueue(startVertex);
while (front <= rear) {
int currentVertex = dequeue();
printf("Visited %d\n", currentVertex);
for (int i = 0; i < n; i++) {
if (adjMatrix[currentVertex][i] == 1 && !visited[i]) {
visited[i] = 1;
enqueue(i);
}
}
}
}
int main() {
n = 6; // Misalnya, jumlah simpul adalah 6
// Matriks ketetanggaan untuk graf
int adjMatrixExample[6][6] = {
{0, 1, 1, 0, 0, 0},
{1, 0, 1, 1, 1, 0},
{1, 1, 0, 0, 1, 0},
{0, 1, 0, 0, 1, 1},
{0, 1, 1, 1, 0, 1},
{0, 0, 0, 1, 1, 0}
};
// Copy data ke adjMatrix
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
adjMatrix[i][j] = adjMatrixExample[i][j];
BFS(0); // Mulai BFS dari simpul 0
return 0;
}Depth First Search (DFS) adalah algoritma penelusuran graf yang dimulai dari simpul awal dan mengeksplorasi sedalam mungkin di setiap cabang sebelum kembali. DFS menggunakan struktur data tumpukan (stack) atau rekursi.
- Mulai dari simpul awal dan tandai sebagai terkunjungi.
- Untuk setiap tetangga simpul tersebut:
- Jika tetangga belum dikunjungi, panggil DFS secara rekursif pada tetangga tersebut.
Implementasi DFS dalam C:
#include <stdio.h>
#include <stdlib.h>
int visited[MAX] = {0};
int adjMatrix[MAX][MAX];
int n; // Jumlah simpul
void DFS(int vertex) {
visited[vertex] = 1;
printf("Visited %d\n", vertex);
for (int i = 0; i < n; i++) {
if (adjMatrix[vertex][i] == 1 && !visited[i]) {
DFS(i);
}
}
}
int main() {
n = 6; // Misalnya, jumlah simpul adalah 6
// Matriks ketetanggaan untuk graf
int adjMatrixExample[6][6] = {
{0, 1, 1, 0, 0, 0},
{1, 0, 1, 1, 1, 0},
{1, 1, 0, 0, 1, 0},
{0, 1, 0, 0, 1, 1},
{0, 1, 1, 1, 0, 1},
{0, 0, 0, 1, 1, 0}
};
// Copy data ke adjMatrix
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
adjMatrix[i][j] = adjMatrixExample[i][j];
DFS(0); // Mulai DFS dari simpul 0
return 0;
}- Menggunakan antrian (queue).
- Baik untuk menemukan lintasan terpendek dalam graf tidak berbobot.
- Mengeksplorasi semua tetangga di setiap tingkat sebelum pindah ke tingkat berikutnya.
- Menggunakan tumpukan (stack) atau rekursi.
- Baik untuk mengeksplorasi sedalam mungkin dalam graf.
- Dapat terjebak dalam siklus jika graf mengandung siklus dan tidak ditangani dengan baik.
Graf adalah struktur data penting yang digunakan untuk merepresentasikan berbagai hubungan dan proses dalam dunia nyata. BFS dan DFS adalah dua algoritma dasar untuk penelusuran graf yang masing-masing memiliki keunggulan dan kegunaan tergantung pada aplikasi yang diinginkan. Pemahaman mendalam tentang graf dan algoritma penelusurannya sangat penting bagi pengembang perangkat lunak dan ilmuwan komputer.