PythonLibs

Somewhat useful python custom libraries

Vector

• Create Vectors and use operations in any way you want.
• Convenient, no dimensions limits, easily manipulated.

Use it as an object, list, dictionary, tuple, whatever, anything works.

Vector basics

Declaration

from vectors import *
foo = Vector(5,7)
print(foo)

>>> Vector2(5, 7)

Or choose your own way to create a Vector

a = Vector([3,4,6])
b = Vector({'y':8, 'x':3})
c = Vector(1)
d = Vector()

>>> Vector3(3, 4, 6)
>>> Vector2(3, 8)
>>> Vector1(1)
>>> Vector0()

Basic operations

• Working operators:

bool abs sum ceil floor round invert str == -x and or % * + - / // ** [x] [x]=x len hash repr < > <= >= ~

Just think of them as normal numbers:

a = Vector(1,2)
b = Vector(3,4)

print(a+b)

>>> Vector2(4, 6)

Not the same dimension? Doesn't matter.

• 0 will be the default value for missing values

a = Vector(1,2,3)
b = Vector(5)

print(a-b)

>>> Vector3(-4, 2, 3)

• empty values will be ignored for divisions (no divisions by 0)
  operators: / // %

a = Vector(6,2,1,0)
b = Vector(2)

print(a/b) # a//b also works btw

>>> Vector4(3.0, 2, 1, 0)

Coordinates

Coordinates are saved in Vector.coords

foo = Vector(7,8,9)
print(foo.coords)

>>> [7, 8, 9]

However, that was the polically correct way, which is boring. Again, do it however you want:

foo = Vector(7,8,9)
for v in foo:
    print(v)

7 8 9

Or unpacking the values

def bar(x,y,z):
    print(x+y+z)

foo = Vector(7,8,9)
bar(*foo)

24

Individual coordinates

You get it at this point...

foo = Vector(7,8,9)

foo.coords[0] = 1
foo[1] = 2
foo.z = 3

print(foo)

print(foo.coords[0], foo[1], foo.z)

Vector3(1, 2, 3)
1 2 3

Comparison

Operators such as == != are self-explanatory,

a = Vector(1,2,3)
b = Vector(3,3,3)
c = Vector(2,1,0)
print(a == b-c)

>>> True

But some aren't really black and white:

• Ambigous operators:

bool(foo) will always return True

if (Vector(0)): True

This allows simpler boolean operations:

vec and "Correct" or "Incorrect"

a>b will return sum(a)>sum(b) (sum of all coordinates)

Vector(-8,8) > Vector(1) = False

Math aliases

Vectors are compatible with the math lib

import math

foo = Vector(1.3, 2.8)
print(math.floor(foo))
print(math.ceil(foo))

Vector2(1, 2)
Vector2(2, 3)

It is also possible to use these methods without the library

print(foo.floor())
print(foo.ceil())

Copying

Use either copy clone new
Or you can even use Vector(vec):

foo = Vector(1,2)

a = foo.copy()
b = foo.clone()
c = foo.new()
d = Vector(foo)

foo.x = 0

print(a,b,c,d)
print(foo)

Vector2(1, 2) Vector2(1, 2) Vector2(1, 2) Vector2(1, 2)
Vector2(0, 2)

Methods:

bounds(*vectors):

Returns the minimum and maximum vectors of all given vectors:
-> (min: Vector, max: Vector)

a = Vector(1,2,3)
b = Vector(3,3,2)
c = Vector(2,1,0)
print(a.bounds(b,c)) # using self
print(Vector.bounds(a,b,c))

>>> (Vector3(1, 1, 0), Vector3(3, 3, 3))
>>> (Vector3(1, 1, 0), Vector3(3, 3, 3))

dot(*vectors):

(<=> length of a vector)
Dot vectors of one or multiple vectors:
-> scalar: int

a = Vector(1,2,3)
b = Vector(3,3,2)
print(a.dot(b))

>>> 15

cross(vecA, vecB):

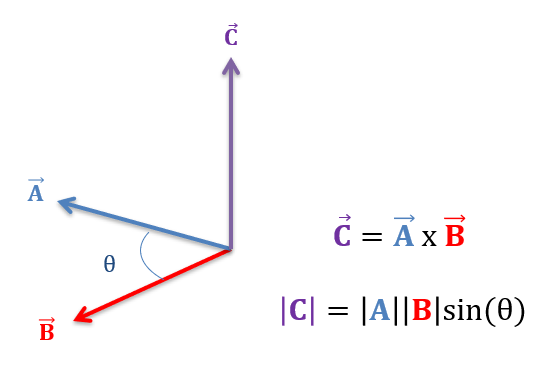
⚠️ Only for Vector3

Cross product of 2 Vectors: -> crossed: Vector

```py a = Vector(1,2,3) b = Vector(3,3,2) print(a.cross(b)) ``` ```py >>> Vector3(-5, 7, -3) ```

angle(vecA, vecB):

⚠️ Only for Vector2

Returns the angle between 2 vectors:
-> radians: float

a = Vector(1,0)
b = Vector(0,1)
print(a.angle(b))

>>> 1.571 # radians

orthogonal(vecA, vecB, approx=0):

⚠️ Only for Vector2

Returns True if both vectors are orthogonal:
(<=> vecA.dot(vecB) <= approx)
-> orthogonal: bool

a = Vector(1,0)
b = Vector(0,1)
print(a.orthogonal(b))

>>> True

lerp(vecA, vecB, time):

Returns the linearly interpolated vector:

a = Vector(6,3)
b = Vector(10,1)
print(a.lerp(b, 0.5))

>>> Vector2(8, 2)

Pointer [WIP]

[Only supported in 2D for now]
An object with a Vector position and a rotation number

arrow = Pointer(Vector(0,0), 0, unit='deg') # radians by default
arrow.move(Vector(5,0))
arrow.rotate(45)
arrow.forward(5)