Initial matmul implementation

[chriselrod]

This is hopefully a fairly simple/clear initial single-threaded implementation.

Running on my laptop:

julia> using Octavian, Gaius

julia> M=K=N=8000; # compilation omitted; you should probably  compile on smaller matrices

julia> A = rand(M,K); B = rand(K,N); C2 = A * B; C1 = similar(C2);

julia> @time(matmul!(C1, A, B)) ≈ C2 # Octavian
 17.426438 seconds
true

julia> @time(blocked_mul!(C1, A, B)) ≈ C2 # Gaius, single threaded
 20.374492 seconds
true

julia> 2e-9M*K*N / 17.426438 # GFLOPS Octavian
58.76129132069332

julia> 2e-9M*K*N / 20.374492 # GFLOPS Gaius
50.2589217929949

julia> M=K=N=4000; # smaller matrices

julia> A = rand(M,K); B = rand(K,N); C2 = A * B; C1 = similar(C2);

julia> @time(matmul!(C1, A, B)) ≈ C2
  2.084635 seconds
true

julia> @time(blocked_mul!(C1, A, B)) ≈ C2
  2.303190 seconds
true

julia> 2e-9M*K*N / 2.084635 # GFLOPS Octavian
61.401636257666226

julia> 2e-9M*K*N / 2.303190 # GFLOPS Octavian
55.57509367442549

julia> versioninfo()
Julia Version 1.7.0-DEV.168
Commit dedf290c99 (2020-12-25 20:12 UTC)
Platform Info:
  OS: Linux (x86_64-linux-gnu)
  CPU: 11th Gen Intel(R) Core(TM) i7-1165G7 @ 2.80GHz
  WORD_SIZE: 64
  LIBM: libopenlibm
  LLVM: libLLVM-11.0.0 (ORCJIT, tigerlake)

Blocking parameters could probably use tuning, it'd need a multi-threading implementation, and we could consider properly packing arrays into tile-major layouts for consecutive memory accesses instead of column-major.
Additionally, Gaius supports complex numbers.

We should also add checks for matrix sizes and call the macro-kernel directly if the arrays aren't that large. This would give a large performance boost at small sizes.
In a similar vein, we could add a "only pack A" implementation to sit between the raw macro-kernel and packing both A and B.

But I figured I'd elicit feedback first on what you think about code clarity, or if you're perhaps interested in taking things from here.

[codecov]

Codecov Report

Merging #6 (adbac62) into master (e2209c4) will decrease coverage by 17.07%.
The diff coverage is 81.57%.

@@             Coverage Diff              @@
##            master       #6       +/-   ##
============================================
- Coverage   100.00%   82.92%   -17.08%     
============================================
  Files            2        7        +5     
  Lines            9      123      +114     
============================================
+ Hits             9      102       +93     
- Misses           0       21       +21     

Impacted Files	Coverage Δ
src/types.jl	44.44% <44.44%> (ø)
src/utils.jl	73.33% <73.33%> (ø)
src/macrokernel.jl	92.30% <92.30%> (ø)
src/block_sizes.jl	94.11% <94.11%> (ø)
src/Octavian.jl	100.00% <100.00%> (ø)
src/matmul.jl	100.00% <100.00%> (ø)
... and 1 more

---

Continue to review full report at Codecov.

Legend - Click here to learn more
Δ = absolute <relative> (impact), ø = not affected, ? = missing data
Powered by Codecov. Last update e2209c4...adbac62. Read the comment docs.

[chriselrod]

Tests failed because they took too long.
Locally, most of the time was spent in the default integer LinearAlgebra.mul! routines I was comparing Octavian's answers to.

But Octavian's functions slow to a crawl when measuring code coverage, so I'll reduce the size range of matrices tested.

[DilumAluthge]

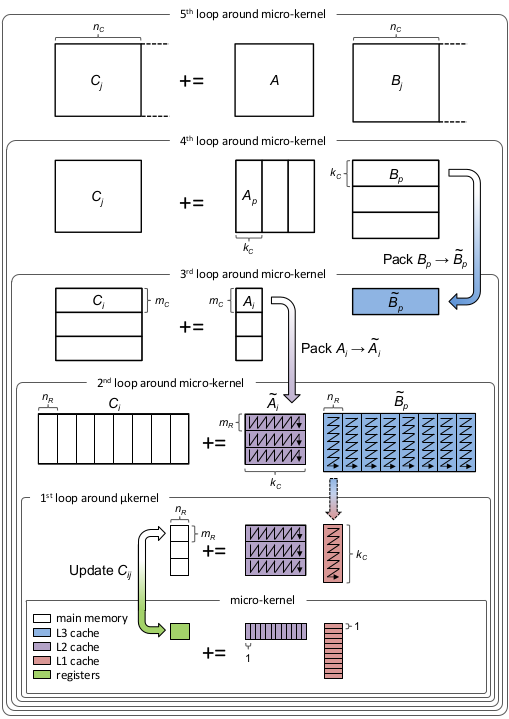
So, working off of the BLIS diagram (which I've pasted at the bottom of this comment), am I correct in saying that the macrokernel in this PR includes both the 1st loop around microkernel and the 2nd loop around microkernel?

This is what I am thinking:

1. The for k ∈ axes(B,1) in the macrokernel is exactly the microkernel from the BLIS diagram.
2. The for n ∈ axes(C,2), m ∈ axes(C,1) in the macrokernel correspond to loop 1 and loop 2 in the BLIS diagram.

Is this correct?

[chriselrod]

Close. Note that the diagram says that the block of C being updated in the microkernel is mᵣ x nᵣ.

If we look at just those three loops written out and say that for k ∈ axes(B,1) corresponds to the microkernel, it might look like mᵣ = nᵣ = 1. But it's important to remember that what LoopVectorization does can look quite different from the loops themselves.
If you can read assembly or llvm, then Cthulhu is a great way to find out what it's actually doing, e.g.

@descend debuginfo=:none Octavian.macrokernel!(C1, A, B, 1.0, 0.0)

This produces (along with a massive amount of other output) the following central k loop:

L1200:
        vmovupd zmm1, zmmword ptr [r15]
        vmovupd zmm0, zmmword ptr [r15 + 64]
        vmovupd zmm2, zmmword ptr [r15 + 128]
        prefetcht0      byte ptr [r15 + r9 - 128]
        vbroadcastsd    zmm3, qword ptr [rsi - 8]
        prefetcht0      byte ptr [r15 + r9 - 64]
        prefetcht0      byte ptr [r15 + r9]
        vfmadd231pd     zmm5, zmm1, zmm3        # zmm5 = (zmm1 * zmm3) + zmm5
        vfmadd231pd     zmm6, zmm0, zmm3        # zmm6 = (zmm0 * zmm3) + zmm6
        vbroadcastsd    zmm4, qword ptr [rdx + rax]
        vfmadd231pd     zmm7, zmm2, zmm3        # zmm7 = (zmm2 * zmm3) + zmm7
        vfmadd231pd     zmm8, zmm1, zmm4        # zmm8 = (zmm1 * zmm4) + zmm8
        vfmadd231pd     zmm9, zmm0, zmm4        # zmm9 = (zmm0 * zmm4) + zmm9
        vfmadd231pd     zmm10, zmm2, zmm4       # zmm10 = (zmm2 * zmm4) + zmm10
        vbroadcastsd    zmm3, qword ptr [rdx + 2*rax]
        vfmadd231pd     zmm11, zmm1, zmm3       # zmm11 = (zmm1 * zmm3) + zmm11
        vfmadd231pd     zmm12, zmm0, zmm3       # zmm12 = (zmm0 * zmm3) + zmm12
        vfmadd231pd     zmm13, zmm2, zmm3       # zmm13 = (zmm2 * zmm3) + zmm13
        vbroadcastsd    zmm3, qword ptr [rdx + rdi]
        vfmadd231pd     zmm14, zmm1, zmm3       # zmm14 = (zmm1 * zmm3) + zmm14
        vfmadd231pd     zmm15, zmm0, zmm3       # zmm15 = (zmm0 * zmm3) + zmm15
        vfmadd231pd     zmm16, zmm2, zmm3       # zmm16 = (zmm2 * zmm3) + zmm16
        vbroadcastsd    zmm3, qword ptr [rdx + 4*rax]
        vfmadd231pd     zmm17, zmm1, zmm3       # zmm17 = (zmm1 * zmm3) + zmm17
        vfmadd231pd     zmm18, zmm0, zmm3       # zmm18 = (zmm0 * zmm3) + zmm18
        vfmadd231pd     zmm19, zmm2, zmm3       # zmm19 = (zmm2 * zmm3) + zmm19
        vbroadcastsd    zmm3, qword ptr [rdx + rbx]
        vfmadd231pd     zmm20, zmm1, zmm3       # zmm20 = (zmm1 * zmm3) + zmm20
        vfmadd231pd     zmm21, zmm0, zmm3       # zmm21 = (zmm0 * zmm3) + zmm21
        vfmadd231pd     zmm22, zmm2, zmm3       # zmm22 = (zmm2 * zmm3) + zmm22
        vbroadcastsd    zmm3, qword ptr [rdx + 2*rdi]
        vfmadd231pd     zmm23, zmm1, zmm3       # zmm23 = (zmm1 * zmm3) + zmm23
        vfmadd231pd     zmm24, zmm0, zmm3       # zmm24 = (zmm0 * zmm3) + zmm24
        vbroadcastsd    zmm4, qword ptr [rdx + rcx]
        vfmadd231pd     zmm25, zmm2, zmm3       # zmm25 = (zmm2 * zmm3) + zmm25
        vfmadd231pd     zmm26, zmm1, zmm4       # zmm26 = (zmm1 * zmm4) + zmm26
        vfmadd231pd     zmm27, zmm0, zmm4       # zmm27 = (zmm0 * zmm4) + zmm27
        vfmadd231pd     zmm28, zmm2, zmm4       # zmm28 = (zmm2 * zmm4) + zmm28
        vbroadcastsd    zmm3, qword ptr [rsi + 8*rax - 8]
        vfmadd231pd     zmm29, zmm3, zmm1       # zmm29 = (zmm3 * zmm1) + zmm29
        vfmadd231pd     zmm30, zmm3, zmm0       # zmm30 = (zmm3 * zmm0) + zmm30
        vfmadd231pd     zmm31, zmm2, zmm3       # zmm31 = (zmm2 * zmm3) + zmm31
        add     r15, r8
        mov     rdx, rsi
        add     rsi, 8
        cmp     r15, rbp
        jbe     L1200

This will look different on different CPUs.
I'd be happy to explain in more detail what this says/days or answer questions. But a quick rundown:
The last line above jbe L1200 conditionally jumps to location L1200, which you see at the top. That is, this block of code repeats until the condition becomes false. That is, this defines a loop.

The vfmadd instructions document what they do. You see that they each update a register.

        vfmadd231pd     zmm5, zmm1, zmm3        # zmm5 = (zmm1 * zmm3) + zmm5

I.e., zmm5 += zmm1 * zmm3.
You can tell this is the central loop, updating Cmn += A[m,k] * B[k,n].
Note that a zmm register is 512 bits, i.e. it holds 8 Float64.

We have 27 of these in the loop. That means the block of C getting updated by the microkernel contains 216 elements, not just 1. Specifically, it is a 24 x 9 block of C.
Each iteration of this k loop loads 24 numbers from A, e.g. A[1:24,k]:

        vmovupd zmm1, zmmword ptr [r15]
        vmovupd zmm0, zmmword ptr [r15 + 64]
        vmovupd zmm2, zmmword ptr [r15 + 128]

Then, it loads 9 numbers from B:

        vbroadcastsd    zmm3, qword ptr [rsi - 8]
        vbroadcastsd    zmm4, qword ptr [rdx + rax]
        vbroadcastsd    zmm3, qword ptr [rdx + 2*rax]
        vbroadcastsd    zmm3, qword ptr [rdx + rdi]
        vbroadcastsd    zmm3, qword ptr [rdx + 4*rax]
        vbroadcastsd    zmm3, qword ptr [rdx + rbx]
        vbroadcastsd    zmm3, qword ptr [rdx + 2*rdi]
        vbroadcastsd    zmm4, qword ptr [rdx + rcx]
        vbroadcastsd    zmm3, qword ptr [rsi + 8*rax - 8]

So for each k it would, for example

C[1:24,1] .+= A[1:24,k] * B[k,1]
C[1:24,2] .+= A[1:24,k] * B[k,2]
C[1:24,3] .+= A[1:24,k] * B[k,3]
C[1:24,4] .+= A[1:24,k] * B[k,4]
C[1:24,5] .+= A[1:24,k] * B[k,5]
C[1:24,6] .+= A[1:24,k] * B[k,6]
C[1:24,7] .+= A[1:24,k] * B[k,7]
C[1:24,8] .+= A[1:24,k] * B[k,8]
C[1:24,9] .+= A[1:24,k] * B[k,9]

What's the advantage of doing it this way?
Note that we don't load and store from C at all inside the inner loop.
These 216 numbers sit in the CPU registers and get updated in the each iteration.

For each iteration of k, to update these 216 numbers from C, we only do 3 loads from A and 9 loads from B.
We reuse the 24 numbers loaded from A 9 times before having to replace them, and we reuse each number loaded from B 3 times.
Also, if you look at the naive loops:

for n in axes(C,2)
    for m in axes(C,1)
        Cmn = zero(eltype(C))
        for k in axes(B,1)
            Cmn += A[m,k] * B[k,n]
        end
        C[m,n]  = Cmn
    end
end

You see that we would have to pass over the entire A once for each n in axes(C,2). By instead loading 9 numbers at a time, we pass over A one-ninth as often, meaning this memory reuse also translates to passing through our memory much more slowly.

So the microkernel is fairly sophisticated, but LoopVectorization makes it easy.

[chriselrod]

Also, take a look at the docstring on Octavian.block_sizes

help?> Octavian.block_sizes
  block_sizes(::Type{T}) -> (Mc, Kc, Nc)

  Returns the dimensions of our macrokernel, which iterates over the microkernel. That is, in calculating C = A * B, our macrokernel will be called on Mc × Kc blocks of A, multiplying them with Kc × Nc blocks of B, to update Mc ×
  Nc blocks of C.

  We want these blocks to fit nicely in the cache. There is a lot of room for improvement here, but this initial implementation should work reasonably well.

  The constants LoopVectorization.mᵣ and LoopVectorization.nᵣ are the factors by which LoopVectorization wants to unroll the rows and columns of the microkernel, respectively. LoopVectorization defines these constants by running
  it's analysis on a gemm kernel; they're there for convenience/to make it easier to implement matrix-multiply. It also wants to vectorize the rows by W = VectorizationBase.pick_vector_width_val(T). Thus, the microkernel's
  dimensions are (W * mᵣ) × nᵣ; that is, the microkernel updates a (W * mᵣ) × nᵣ block of C.

  Because the macrokernel iterates over tiles and repeatedly applies the microkernel, we would prefer the macrokernel's dimensions to be an integer multiple of the microkernel's. That is, we want Mc to be an integer multiple of W
  * mᵣ and Nc to be an integer multiple of nᵣ.

  Additionally, we want our blocks of A to fit in the core-local L2 cache. Empirically, I found that when using Float64 arrays, 72 rows works well on Haswell (where W * mᵣ = 8) and 96 works well for Cascadelake (where W * mᵣ =
  24). So I kind of heuristically multiply W * mᵣ by 4 given 32 vector register (as in Cascadelake), which would yield 96, and multiply by 9 otherwise, which would give 72 on Haswell. Ideally, we'd have a better means of picking.
  I suspect relatively small numbers work well because I'm currently using a column-major memory layout for the internal packing arrays. A column-major memory layout means that if our macro-kernel had a lot of rows, moving across
  columns would involve reading memory far apart, moving across memory pages more rapidly, hitting the TLB harder. This is why libraries like OpenBLAS and BLIS don't use a column-major layout, but reshape into a 3-d array, e.g. A
  will be reshaped into a Mᵣ × Kc × (Mc ÷ Mᵣ) array (also sometimes referred to as a tile-major matrix), so that all memory reads happen in consecutive memory locations.

  Now that we have Mc, we use it and the L2 cache size to calculate Kc, but shave off a percent to leave room in the cache for some other things.

  We want out blocks of B to fir in the L3 cache, so we can use the L3 cache-size and Kc to similarly calculate Nc, with the additional note that we also divide and multiply by nᵣ to ensure that Nc is an integer multiple of nᵣ.

[DilumAluthge]

I'm merging this so I can make some new PRs on top of this, but we'll continue this conversation; I have some reading to do 😂

[chriselrod]

Sure, and as always I'm happy to answer questions in issues/prs/on zulip.

I'll release a new version of VectorizationBase soon that adds a cache-inclusivity vector and then update the block sizes function correspondingly.