Solving a system of linear equations Ax=b using naive method, SciPy and NumPy
This repository contains Python scripts to solve a system of linear equations AX = b using different methods, including the naive approach, NumPy, and SciPy. The goal is to compare the execution times for solving banded matrices of various dimensions.
| Matrices Dimensions | X = A^-1b | NumPy | SciPy |
|---|---|---|---|
| A(10x10) | ? | ? | ? |
| A(100x100) | ? | ? | ? |
| A(1000x1000) | ? | ? | ? |
| A(10000x10000) | ? | ? | ? |
| A(100000x100000) | ? | ? | ? |
- [20 marks] Solve by finding the inverse of the matrix A and then multiplying it by the vector b to get the solution.
- [20 marks] Solve these systems using NumPy's linalg.solve module and record the empirical time it takes to produce the solution.
- [20 marks] Convert the banded matrix A into the form Ab and use SciPy's linalg.solve_banded to solve the system AX=b. Note down the empirical time it takes to produce a solution.
- [20 marks] Plot your experiment using a suitable plot by using matplotlib. Properly label this plot so that it is self-readable.
- [20 marks] Provide a conclusion of your experiment based on the results you measured.
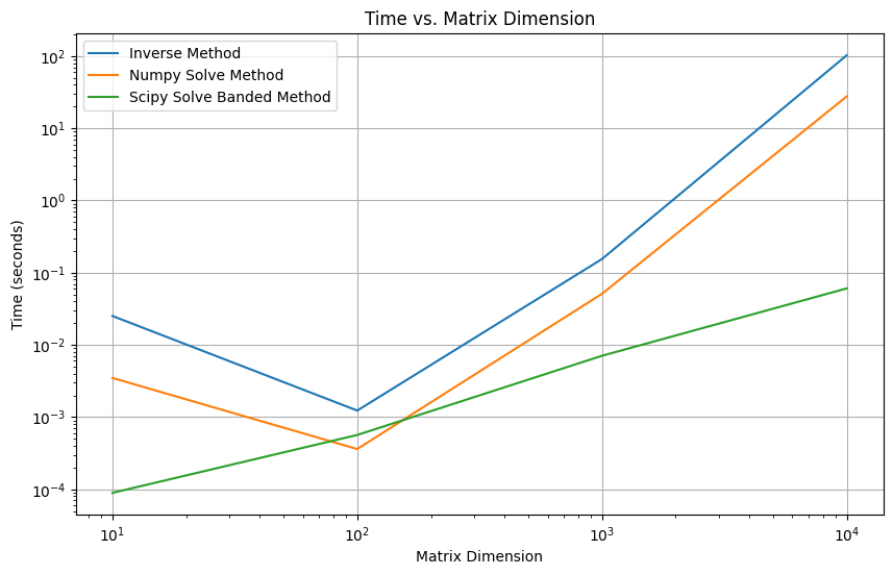
In this experiment, I investigated the performance of three different methods for solving matrix equations: the inverse matrix method, NumPy's linalg.solve method, and SciPy's linalg.solve_banded method.
I observed that for the smallest matrix dimension, all methods performed well, but SciPy was the best among the three, taking less than 0.0001 seconds. The other two methods were slower in comparison but still fast enough to make no matter. The 100x100 dimension gave a very interesting result, as it was the only dimension where a method was faster than SciPy. NumPy took less time here, and as expected, the naive method was the slowest. However, as the matrix dimensions increased to 1000x1000 and beyond, the performance of the inverse matrix method degraded significantly, leading to longer computation times and potential numerical instability. NumPy's linalg.solve method demonstrated better scalability with larger matrix dimensions compared to the inverse matrix method, while SciPy's linalg.solve_banded method showed promising results for banded matrices. It is important to note that I was unable to perform 100000x100000 due to time and hardware restraints. However, seeing the general trend of the graph, I can safely say that the SciPy method would be the fastest, while the naive method would be painstakingly slow, with NumPy falling somewhere between the two.
This is what the output looks like: