Geometry

Session

Session Record

Outlines

• Geometry
  • Outlines
  • Remarks
    • Elements
    • Angles
    • Constants
    • Trigonometric Laws
  • Dot Product (inner product)
  • Cross Product (outer product)
  • Complex Data Type
  • Operations
  • Distance
  • Intersection
  • Problems To Solve
  • Resources

Remarks

Elements

Name	Description
Point	A point in the plane
Line segment	A line segment is a finite line with two endpoints
Ray	A ray is a line with one endpoint and extends infinitely in one direction
Line	A line is a set of points that are equidistant from a fixed point
Plane	A plane is a flat surface that extends infinitely far
Vector	A vector is a quantity that has magnitude and direction

Angles

Name	Description
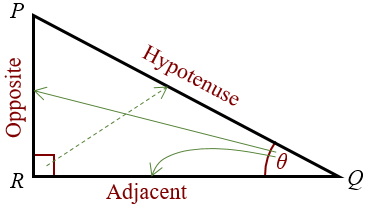
Radians	Radians are a unit of angular measure, used in many areas of mathematics. One radian is the angle at the center of a circle subtended by an arc equal in length to the radius of the circle.
Degrees	Degrees are a unit of angular measure, representing $1/360$ of a full rotation.

atan(y/x)	atan2(y, x)
from $[-\pi/2, \pi/2]$	from $[-\pi, \pi]$

Constants

Name	Description
PI	The value of $\pi$
EPS	The value of $10^{-9}$

Trigonometric Laws

Laws	Description
Law of cosines	$c^2 = a^2 + b^2 - 2abCos(C)$
Law of sines	$\frac{a}{Sin(A)} = \frac{b}{Sin(B)} = \frac{c}{Sin(C)}$
Pythagorean theorem	$a^2 + b^2 = c^2$
sine	$Sin(\theta) = \frac{Opposite}{Hypotenuse}$
cosine	$Cos(\theta) = \frac{Adjacent}{Hypotenuse}$
tangent	$Tan(\theta) = \frac{Opposite}{Adjacent}$

Dot Product (inner product)

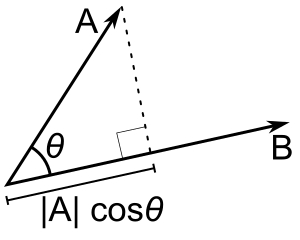
• The dot product of two vectors is simply the sum of the products of the corresponding elements. For example, the dot product of $(x_1, y_1)$ and $(x_2, y_2)$ is $x_1 \times x_2 + y_1 \times y_2$.
• Note that this is not a vector, but is simply a single number (called a scalar).
• The reason this is useful is that the dot product, $A \cdot B = |A||B|Cos(θ)$, where $θ$ is the angle between the $A$ and $B$.

Property	Description
$A \cdot B = B \cdot A$	Commutative
$A \cdot (B + C) = A \cdot B + A \cdot C$	Distributive

These cases depending on cos() domain:

cases	description
$A \cdot B = 0$	$θ = 90^{\circ}$
$A \cdot B > 0$	$θ < 90^{\circ}$
$A \cdot B < 0$	$θ > 90^{\circ}$

Cross Product (outer product)

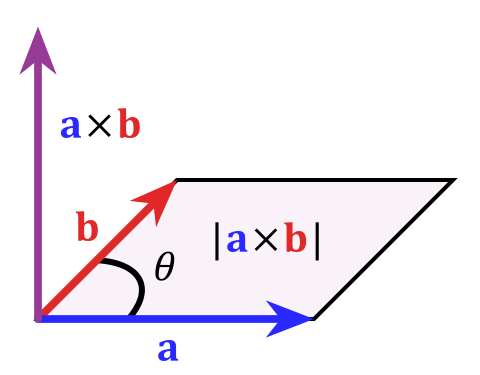
• The cross product of two 2-D vectors is $x_1 \times y_2 - y_1 \times x_2$ = $A \times B$ = $|A||B|Sin(θ)$
• Technically, the cross product is actually a vector
• Since we’re only working with 2-D geometry for now, we’ll ignore this fact, and use it like a scalar.
• the absolute value of the cross product is the area of the parallelogram formed by the two vectors.
• The direction of the cross product is perpendicular to the plane formed by the two vectors.
• The direction of the cross product is determined by the right-hand rule.
• The magnitude of the cross product is the area of the parallelogram formed by the two vectors.
• The magnitude of the cross product is also equal to the determinant of the matrix formed by the two vectors.

Property	Description
$A \times B = -B \times A$	Anti-commutative
$A \times (B + C) = A \times B + A \times C$	Distributive

These cases depending on sin() domain:

cases	description
$A \times B = 0$	$θ = 0^{\circ}$ or $θ = 180^{\circ}$
$A \times B > 0$	$θ < 180^{\circ}$ (convex)
$A \times B < 0$	$θ > 180^{\circ}$ (concave)

Complex Data Type

complex numbers are a data type that is used to represent a number that can be expressed in the form $a + bi$, where $a$ is the real part and $b$ is the imaginary part. The imaginary unit is denoted by $i$, and it is defined by the equation $i^2 = -1$.

Function	Return
real()	Returns the real part of the complex number (X) $*$
imag()	Returns the imaginary part of the complex number (Y) $*$
abs()	Returns the absolute value of the complex number (length)
arg()	Returns the argument of the complex number (angle)
conj()	Returns the conjugate of the complex number (fliping the sign of imaginary part)
norm()	Returns the norm of the complex number (squared length)
polar()	Returns the polar coordinates of the complex number (length and angle)

Note: $*$ The real and imaginary parts of a complex number can be accessed using the real() and imag() methods respectively.

Example: complex.cpp

Operations

• Rotation
• Reflection

Distance

• distance between two points
  • Euclidean distance
• distance point c to line segment ab
  • distance point c to line ab
  • distance point c to segment ab

Intersection

• functions
• counter-clockwise test

Problems To Solve

• A. Where do I Turn? (cross product)
• B. Arpa and an exam about geometry (cross product)
• Closest Distance
• problem
• problem

Resources

• cp-algorithms
• Topcoder Geometry Part-1
• Topcoder Geometry Part-2
• Topcoder Geometry Part-3
• Mathisfun