Python-based-intramurals-scheduling-project-using-bipartite-matching-algorithm

Problem Statement

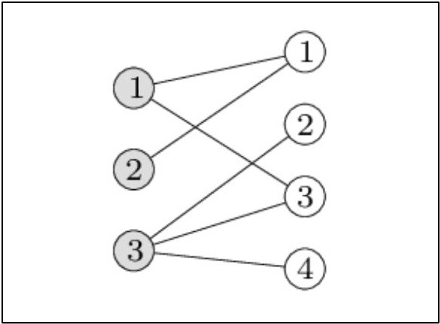
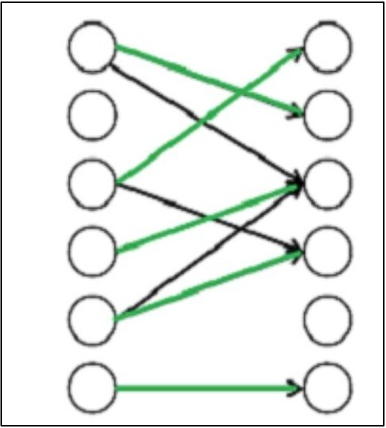
It has been difficult for Whitworth University recreation department to develop ideal schedules that allow each intramural team to play at least once or twice a week and match up with another team. I discovered the best optimum pair solutions by applying the Bipartite Matching Algorithm. Data received from the quadratics survey are saved in CSV files.

Bipartie Matching Algorithm

Finding the maximum matching in a bipartite graph is possible through bipartite matching. In order to expand the size of the matching, the algorithm iteratively searches the network for augmenting pathways. In a graph, a matching is a collection of edges where no two edges meet at the same endpoint. A matching with the most edges is referred to as a maximum matching.

The method begins by looking for a random matching M. A path that alternates between edges in M and edges not in M and starts and finishes at mismatched vertices is known as an augmenting path. In the event that such a path is discovered, the algorithm increases the matching by flipping the edges along the path, producing a greater matching. When there is no longer an augmenting path, the procedure is repeated, at which time the algorithm has discovered a maximum matching.

Pseudocode looks something like this:

• Initialize the matching M to be the empty set.
• While there exists an augmenting path P in the graph: a. Find an augmenting path P from the unmatched left vertices to the unmatched right vertices. b. Add the augmenting path P to the matching M.
• Return the matching M.

Purpose and goals:

1. Utilize the information I received in CS classes that were algorithm-focused
2. Solve real world occuring problems
3. Provides programming utility and efficiency towards the client (Todd Sandberg, Director of University recreation department)
4. Create an executable files that can be accessed by the client (needs to be done)
5. Analyze the data and give the most optimal schedule through bipartite matching
6. Recreate the Bipartite matching algorithm (Modified to match our needs and goals)
7. Make sure the program works for every cases including:
   1. Any amount of sports
   2. Any given days
   3. Any amount of teams

Running the program

For now:

1. Make sure that Python are installed in the device
2. Install some extensions (Panda, Numpy, Xlsx)
3. Copy the csv path to the data
4. Run the program by clicking run
5. 35 different excel files should be generated by now
6. 35 files are earned through 7 days X 5 different sports

Assumption:

• I'm assuming that the U-Rec have some experience with working with executable or .py files
• As I got to know Through my friend who works at U-rec, The U-Rec has some software training such as fusion software that are more complex. This executable file would be easily implemented by U-Rec
• Program assumption:
  1. I assume that the name of each time are unique
  2. U-Rec will not change the way they gather all the data (Qualdratics Survey)
  3. Each team needs to have game at least 1-2x
  4. This is only generated for regular season (excluding playoffs)

Functions:

1. Check: returning a (n)^2 2Dimensional list where n is the number of teams
2. common: Finding common time between 2 teams through boolean (pairing compatibilty [True/False])
3. filter: Returning a list of size (number of team) that is set to -1 as default
4. findpossiblematch: Checking the pairing compatibility of each teams and change the value of -1 to the index of the team that each team is playing against
5. common_time : After finding the compatible pairings and it has been stabilized, then common time between two teams will be determined
6. Others:
   • Reading and Printing the data to excel sheet
   • Panda commands

Works Cited:

1. https://www.geeksforgeeks.org/maximum-bipartite-matching/ (Bipartite matching explenation)
2. https://xlsxwriter.readthedocs.io/working_with_pandas.html - xlsx writer extension
3. Panda library

Accomplishment:

I have contacted the U-Rec and they agreed to use this program next semester. It will help the efficiency of creating a stable schedule.