Improve differentiation between required and optional

[lars-reimann]

Is your feature request related to a problem?

The formula we are using right now is overcomplicated and does not always work well.

Desired solution

When checking whether the set annotation was correct, we basically just looked at the two topmost bars of the value histogram. Thus, the formula should only depend on how often the most common value is used ($c_1$) and how often the second most common value is used ($c_2$)

For example, we could have these two checks that must both be true:

$$ c_1 + c_2 \geq 10 $$

$$ \frac{c_1-c_2}{c_1+c_2} \geq 0.1 $$

The first check would ensure we have enough data and the second that there is a clear most common value.

Possible alternatives (optional)

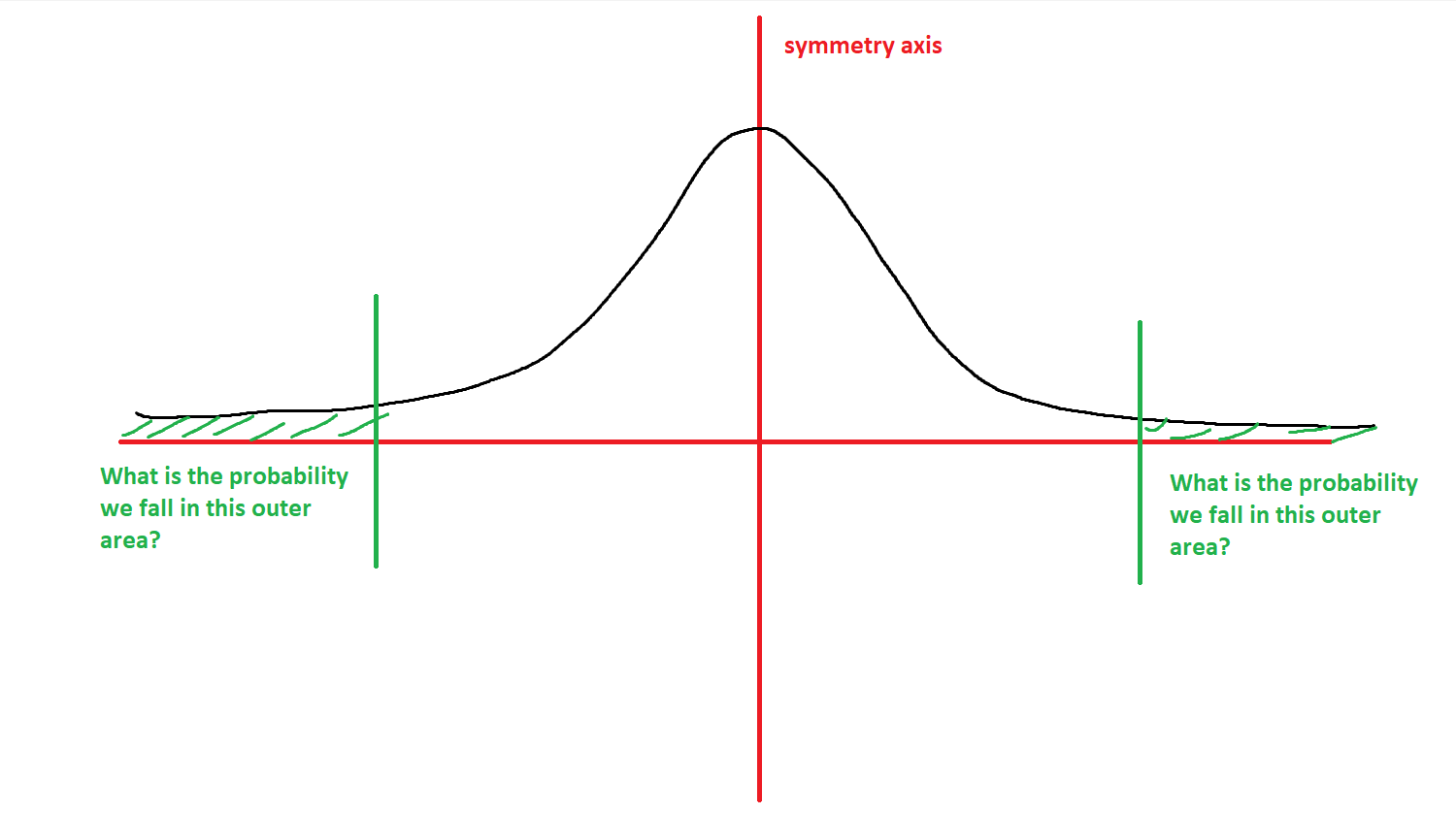
Random idea: Maybe we can use the same method here as to determine whether a coin is fair. If we determine the coin is fair (50% vs. 50%), we make the parameter required (default assumption). Otherwise, we make it optional.

We could determine the probability that a fair coin would produce this distribution (or an even worse spread) and compare it to some significance level $s$ (see https://stats.stackexchange.com/a/21606). If the probability is less than the significance level, we make the parameter optional. Otherwise, we make it required. Said probability would be

$$ 2\sum_{k=c_1}^{c_1+c_2}{\binom{c_1+c_2}{k}(\frac{1}{2})^{c_1+c_2}} $$

Null hypothesis $H_0$: The two most common values occur equally often.
Significance level $s$: If the computed probability is less than or equal to this value, we reject the null hypothesis.

Screenshots (optional)

Additional Context (optional)

Related issues:

• Required Annotation with clear default value #842
• @Optional:None is generated where @Required is expected #828
• Generated @required annotation even though there is a clear most common value #822

[github-actions]

🎉 This issue has been resolved in version 1.41.0 🎉

The release is available on GitHub release

Your semantic-release bot 📦🚀