Possible Julia Multithreading issue exposed by MTK generated functions? #487
Description
Here's an odd case:
using ModelingToolkit, LinearAlgebra, SparseArrays
# Define the constants for the PDE
const α₂ = 1.0
const α₃ = 1.0
const β₁ = 1.0
const β₂ = 1.0
const β₃ = 1.0
const r₁ = 1.0
const r₂ = 1.0
const _DD = 100.0
const γ₁ = 0.1
const γ₂ = 0.1
const γ₃ = 0.1
const N = 16
const X = reshape([i for i in 1:N for j in 1:N],N,N)
const Y = reshape([j for i in 1:N for j in 1:N],N,N)
const α₁ = 1.0.*(X.>=4*N/5)
const Mx = Tridiagonal([1.0 for i in 1:N-1],[-2.0 for i in 1:N],[1.0 for i in 1:N-1])
const My = copy(Mx)
Mx[2,1] = 2.0
Mx[end-1,end] = 2.0
My[1,2] = 2.0
My[end,end-1] = 2.0
# Define the discretized PDE as an ODE function
function f!(du,u,p,t)
A = @view u[:,:,1]
B = @view u[:,:,2]
C = @view u[:,:,3]
dA = @view du[:,:,1]
dB = @view du[:,:,2]
dC = @view du[:,:,3]
mul!(MyA,My,A)
mul!(AMx,A,Mx)
@. DA = _DD*(MyA + AMx)
@. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C
@. dB = α₂ - β₂*B - r₁*A*B + r₂*C
@. dC = α₃ - β₃*C + r₁*A*B - r₂*C
end
# Define the initial condition as normal arrays
@variables du[1:N,1:N,1:3] u[1:N,1:N,1:3] MyA[1:N,1:N] AMx[1:N,1:N] DA[1:N,1:N] p t
f!(du,u,nothing,0.0)
jac = sparse(ModelingToolkit.jacobian(vec(du),vec(u)))
fjac = eval(ModelingToolkit.build_function(jac,u,parallel=ModelingToolkit.SerialForm())[2])
multithreadedfjac = eval(ModelingToolkit.build_function(jac,u,parallel=ModelingToolkit.MultithreadedForm())[2])
using OrdinaryDiffEq
u0 = zeros(N,N,3)
MyA = zeros(N,N);
AMx = zeros(N,N);
DA = zeros(N,N);
prob = ODEProblem(f!,u0,(0.0,10.0))
prob_jac = ODEProblem(ODEFunction(f!,jac = (du,u,p,t) -> fjac(du,u), jac_prototype = similar(jac,Float64)),u0,(0.0,10.0))
using BenchmarkTools
@btime solve(prob, TRBDF2(autodiff=false)) # 459.697 ms (25704 allocations: 10.46 MiB)
@btime solve(prob_jac, TRBDF2()) # 35.869 ms (7194 allocations: 25.10 MiB)Wow so fast right? But if we use the multithreaded one...
prob_jac = ODEProblem(ODEFunction(f!,jac = (du,u,p,t) -> multithreadedfjac(du,u), jac_prototype = similar(jac,Float64)),u0,(0.0,10.0))
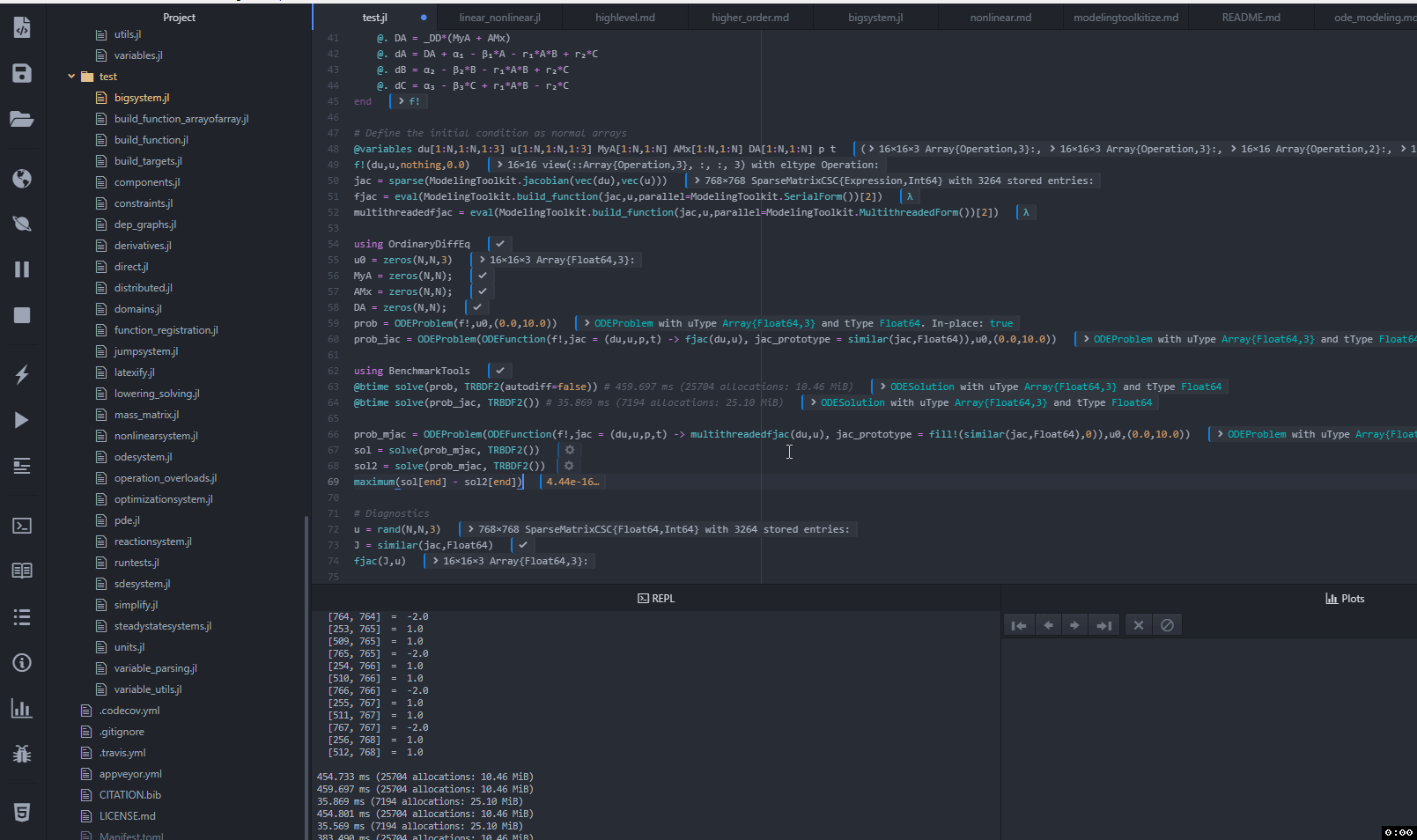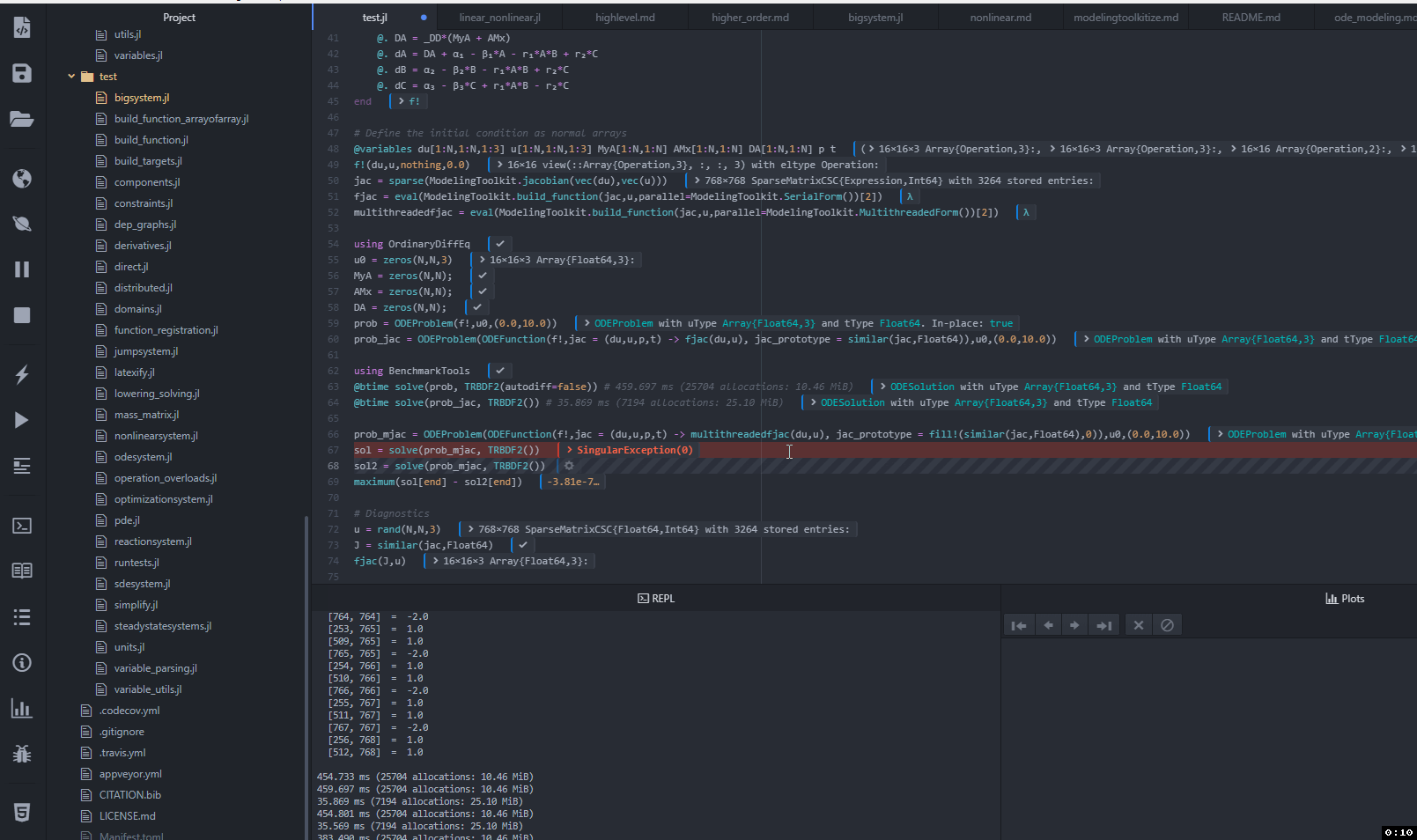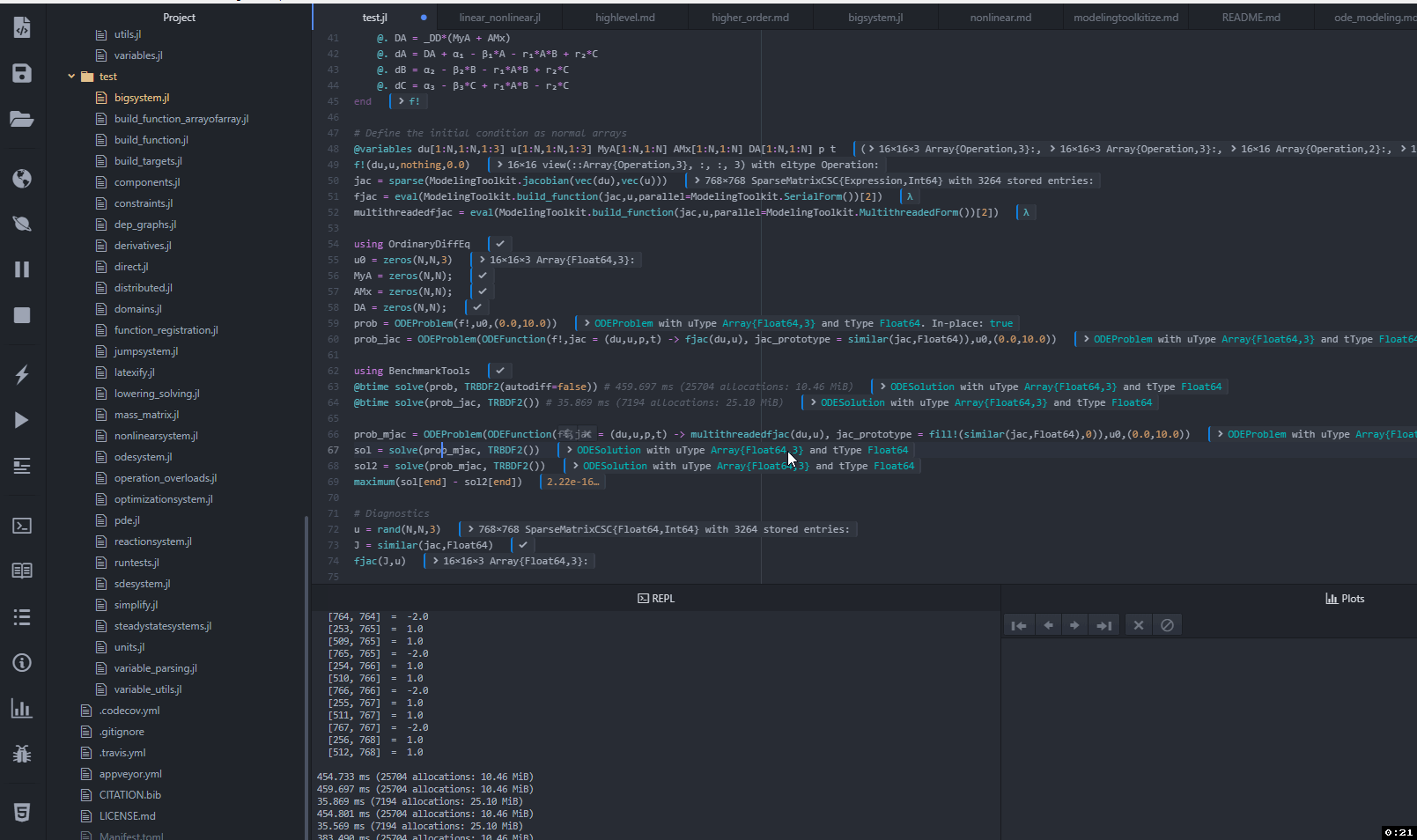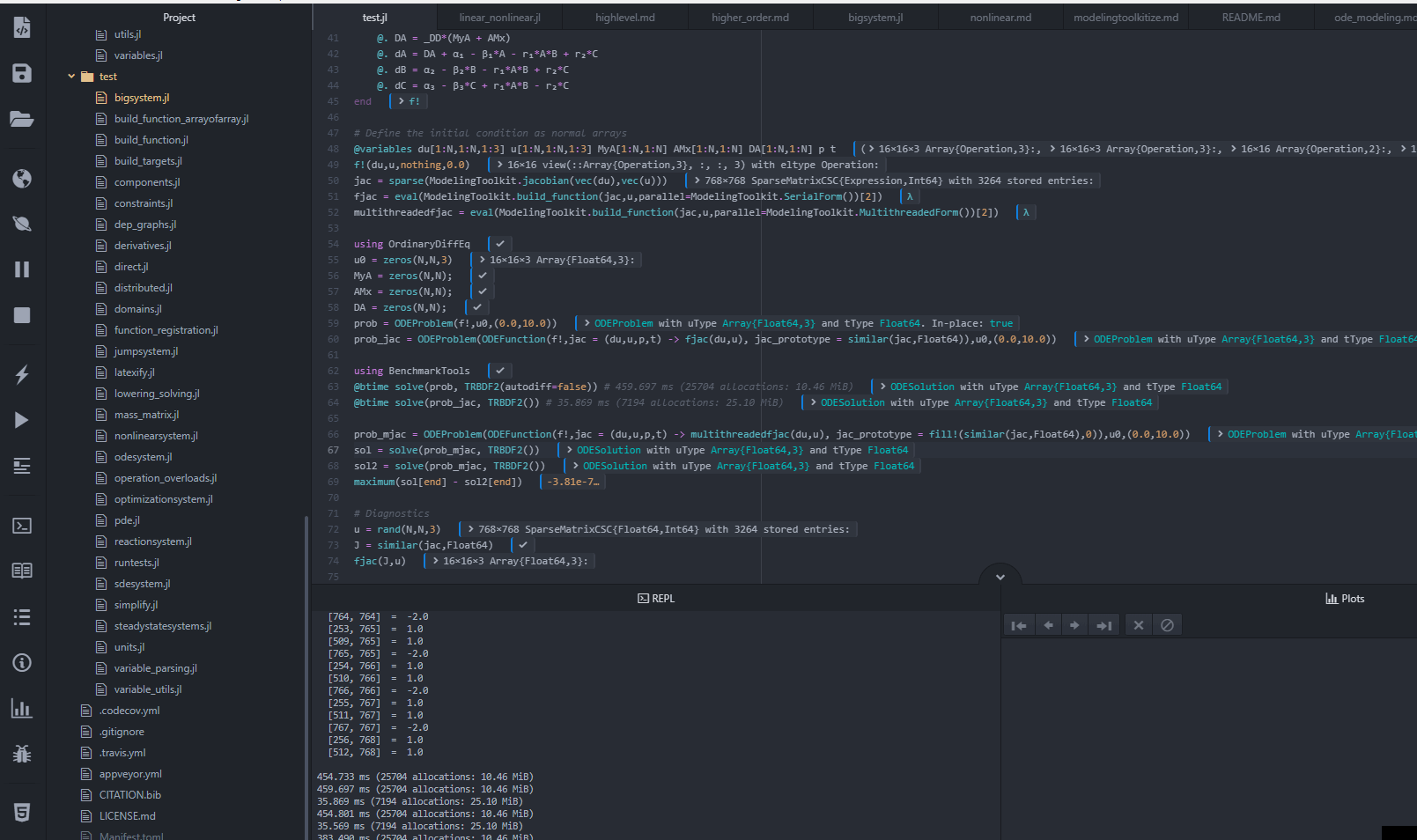
@btime solve(prob_mjac, TRBDF2()) # SingularExceptionIf you run it 10's of times you randomly hit singular exceptions here and there, which is weird because the result given our calculations should be completely independent of multithreading. Here's what it looks like:
Boom, this has errors, while not multithreading does not. However, if I isolate the two functions, I can see that they aren't just close, they produce the exact same values:
# Diagnostics
u = rand(N,N,3)
J = similar(jac,Float64)
fjac(J,u)
J2 = similar(jac,Float64)
multithreadedfjac(J2,u)
maximum(J - J2) == 0
using FiniteDiff
J3 = Array(similar(jac,Float64))
FiniteDiff.finite_difference_jacobian!(J3,(du,u)->f!(du,u,nothing,nothing),u)
maximum(J2 .- Array(J)) < 1e-5