No method matching operation(::Sym{Real, Nothing}) error during index reduction

[JKRT]

Hi!

I have the following model (not sure if it is an error but I have gotten similar models to work using DifferentialEquations.jl (bare bones) ):

using ModelingToolkit
using DiffEqBase
using DifferentialEquations
function SimpleCircuitModel(tspan = (0.0, 1.0))
  pars = ModelingToolkit.@parameters((f, A, C, R1, L, R2, t)) 
  vars = ModelingToolkit.@variables((u2(t), i2(t), u4, u3, i1, u, u1, i))
  der = Differential(t)
  eqs = [
    der(u2) ~ i1 * (C^-1),
    der(i2) ~ u4 * (L^-1),
    0 ~ u - (u4 + u3),
    0 ~ u3 - R2 * i2,
    0 ~ u1 - R1 * i1,
    0 ~ u - A * sin(((2.0 * 3.1415) * f) * t),
    0 ~ u - (u1 + u2),
    0 ~ i - (i2 + i1),
  ]
  nonLinearSystem = ModelingToolkit.ODESystem(
    eqs,
    t,
    vars,
    pars,
    name = :($(Symbol("SimpleCircuit"))),
  )
  params = Dict(
    f => 1.0,
    A => 12.0,
    C => 1.0,
    R1 => 10.0,
    L => 0.01,
    R2 => 100.0,
    t => tspan[1],
  )
  initialValues = [
    u4 => 0.007,
    u3 => 0.0,
    i1 => 0.0,
    u => 0.0,
    u1 => 0.0,
    i => 0.0,
    u2 => 0.0,
    i2 => 0.0,
  ]
  firstOrderSystem = ModelingToolkit.ode_order_lowering(nonLinearSystem)
  reducedSystem = ModelingToolkit.dae_index_lowering(firstOrderSystem)
  problem = ModelingToolkit.ODEProblem(reducedSystem , initialValues, tspan, params)
  return problem
end
function SimpleCircuitSimulate(tspan = (0.0, 10.0))
  problem = SimpleCircuitModel(tspan)
  return solve(problem, Tsit5())
end
SimpleCircuitSimulate()

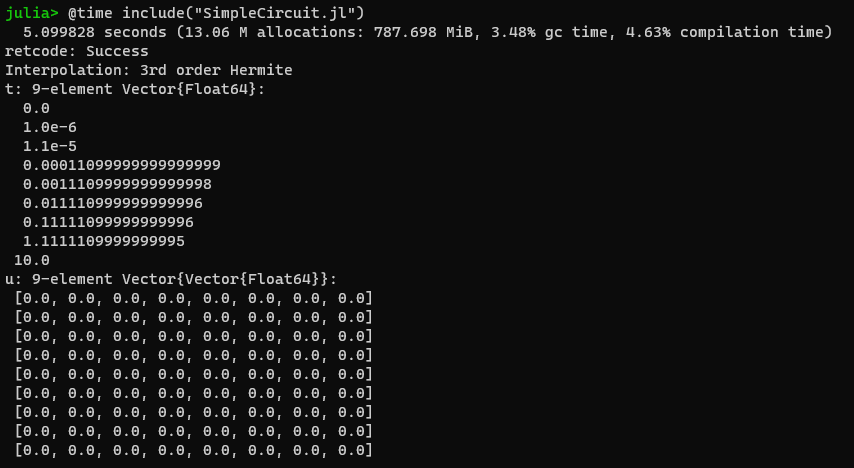
Currently running this results in the following error:

julia> @time include("SimpleCircuit.jl")
ERROR: LoadError: MethodError: no method matching operation(::Sym{Real, Nothing})
Closest candidates are:
  operation(::Term) at C:\Users\John\.julia\packages\SymbolicUtils\9iQGH\src\types.jl:338
  operation(::SymbolicUtils.Add) at C:\Users\John\.julia\packages\SymbolicUtils\9iQGH\src\types.jl:600
  operation(::SymbolicUtils.Mul) at C:\Users\John\.julia\packages\SymbolicUtils\9iQGH\src\types.jl:743

If I make a small change that is,

  firstOrderSystem = ModelingToolkit.ode_order_lowering(nonLinearSystem)
#  reducedSystem = ModelingToolkit.dae_index_lowering(firstOrderSystem)
  problem = ModelingToolkit.ODEProblem(firstOrderSystem, initialValues, tspan, params)
  return problem

It seems that I am able to generate the problem, however the simulation results are wrong

Edit:

Another model with a similar problem:

using ModelingToolkit
using DiffEqBase
using DifferentialEquations
function SimpleMechanicalSystemModel(tspan = (0.0, 1.0))
  pars = ModelingToolkit.@parameters((C, J2, J1, t))
  vars = ModelingToolkit.@variables((
    omega_1(t),
    Phi_1(t),
    Phi_2(t),
    omega_2(t),
    tau_3,
    tau_1,
    tau_2,
    u,
  ))
  der = Differential(t)
  eqs = [
    der(omega_1) ~ (J1^-1) * (tau_1 + tau_2),
    der(Phi_1) ~ omega_1,
    der(Phi_2) ~ omega_2,
    der(omega_2) ~ tau_3 * (J2^-1),
    0 ~ tau_3 - -tau_2,
    0 ~ tau_1 - u,
    0 ~ tau_2 - C * (Phi_2 - Phi_1),
    0 ~ u - t,
  ]
  nonLinearSystem = ModelingToolkit.ODESystem(
    eqs,
    t,
    vars,
    pars,
    name = :($(Symbol("SimpleMechanicalSystem"))),
  )
  pars = Dict(C => 1.0, J2 => 1.0, J1 => 1.0, t => tspan[1])
  initialValues = [
    tau_3 => 0.0,
    tau_1 => 0.0,
    tau_2 => 0.0,
    u => 0.0,
    omega_1 => 0.0,
    Phi_1 => 0.0,
    Phi_2 => 0.0,
    omega_2 => 0.0,
  ]
  firstOrderSystem = ModelingToolkit.ode_order_lowering(nonLinearSystem)
  reducedSystem = ModelingToolkit.dae_index_lowering(firstOrderSystem)
  problem = ModelingToolkit.ODEProblem(reducedSystem, initialValues, tspan, pars)
  return problem
end
function SimpleMechanicalSystemSimulate(tspan = (0.0, 1.0))
  problem = SimpleMechanicalSystemModel(tspan)
  return solve(problem, Rodas5())
end

Cheers,
John

[lamorton]

This appears to work. You need to make all the variables explicitly depend on time. It looks like t doesn't belong inside your vars vector, that needs to be declared separately or pulled out. Then the initial condition for t also needs to be removed.

I used structural_simplify to knock out most of the algebraic equations, and then solve the final system with Rodas5 which can handling the remaining 3 equations, one of which is nonlinear algebraic.

  @variables t
  pars = ModelingToolkit.@parameters((f, A, C, R1, L, R2))
  vars = ModelingToolkit.@variables((u2(t), i2(t), u4(t), u3(t), i1(t), u(t), u1(t), i(t)))
  der = Differential(t)
  eqs = [
    der(u2) ~ i1 * (C^-1),
    der(i2) ~ u4 * (L^-1),
    0 ~ u - (u4 + u3),
    0 ~ u3 - R2 * i2,
    0 ~ u1 - R1 * i1,
    0 ~ u - A * sin(((2.0 * 3.1415) * f) * t),
    0 ~ u - (u1 + u2),
    0 ~ i - (i2 + i1),
  ]
  nonLinearSystem = ModelingToolkit.ODESystem(
    eqs,
    t,
    vars,
    pars,
    name = :($(Symbol("SimpleCircuit"))),
  )
  params = Dict(
    f => 1.0,
    A => 12.0,
    C => 1.0,
    R1 => 10.0,
    L => 0.01,
    R2 => 100.0,
  )
  initialValues = [
    u4 => 0.007,
    u3 => 0.0,
    i1 => 0.0,
    u => 0.0,
    u1 => 0.0,
    i => 0.0,
    u2 => 0.0,
    i2 => 0.0,
  ]
  simplifiedSystem = structural_simplify(nonLinearSystem)
  tspan = (0.0, 10.0)
  problem = ModelingToolkit.ODEProblem(reducedSystem , initialValues, tspan, params)

  solution = solve(problem, Rodas5())

Edit: BTW, the ode_order_lowering wasn't doing anything because the equation was already 1st order.

[ChrisRackauckas]

Thanks! Yeah, that could use a better error message.

[lamorton]

There are at least 3 places where a better error message or sanity check might be appropriate. I changed too much at once; let me break it down.

The original error message:

julia> reducedSystem = ModelingToolkit.dae_index_lowering(firstOrderSystem)
ERROR: MethodError: no method matching operation(::Sym{Real, Nothing})

was due to this line where the dependent variables were not explicitly depending on time:

  vars = ModelingToolkit.@variables((u2(t), i2(t), u4, u3, i1, u, u1, i))

Changing that line to

vars = ModelingToolkit.@variables((u2(t), i2(t), u4(t), u3(t), i1(t), u(t), u1(t), i(t)))

makes the lowering succeed and builds the problem. This is where dae_index_lowering could use a better error message (or maybe the ODE constructor should catch this? See more below).

Next the solver complains: This solver is not able to use mass matrices.Exchanging Tsit5 for Rodas5 eliminates that error message.

However, the output is incorrect (full of zero). This is because t is being defined as a parameter instead of a variable. I think a sanity-check of some sort is warranted, but not sure where it belongs.

Putting t into this line instead:

vars = ModelingToolkit.@variables((t, u2(t), i2(t), u4(t), u3(t), i1(t), u(t), u1(t), i(t)))

is a problem as well:

reducedSystem = ModelingToolkit.dae_index_lowering(firstOrderSystem)
ERROR: BoundsError: attempt to access 10-element Vector{ModelingToolkit.SystemStructures.VariableType} at index [0]

I suspect this is happening b/c vars is only supposed to contain dependent variables here:

 nonLinearSystem = ModelingToolkit.ODESystem(
      eqs,
      t,
      vars,
      pars,
      name = :($(Symbol("SimpleCircuit"))),
    )

That may warrant another improved error message.

Finally, moving t to its own line:

@variables t

makes everything succeed. Setting a value for t in params = Dict(...) is ignored at this point.

If, on the other hand, I had left t in pars

    pars = ModelingToolkit.@parameters((f, A, C, R1, L, R2,t)) 

but removed the params = Dict(...) entry for it, I get:

julia> problem = ModelingToolkit.ODEProblem(reducedSystem , initialValues, tspan, params)
ERROR: ArgumentError: Sym{Real, Base.ImmutableDict{DataType, Any}}[t] are missing from the variable map.

Another permutation: if I make t a parameter on its own line but still have the original error (non-explicit time dependence):

    @parameters t
    pars = ModelingToolkit.@parameters((f, A, C, R1, L, R2)) 
    vars = ModelingToolkit.@variables((u2(t), i2(t), u4(t), u3, i1(t), u(t), u1(t), i(t)))

then I do get a nice error message, this time from the ODE constructor:

julia> problem = ModelingToolkit.ODEProblem(reducedSystem , initialValues, tspan, params)
ERROR: ArgumentError: Any[u3(t)] are missing from the variable map.

It's not clear to me why the original situation (where t was a parameter also, but was included in the pars vector) prevents ODEProblem from recognizing that the dependent variables are missing their time-dependence.

[JKRT]

I guess this issue is resolved. The main issue was improper error messages. However, I guess the point you made @lamorton about having to declare t as a variable on its own line is still an issue.

What is the standard here? I come from a Modelica background and I guess I see time as a parameter rather than a variable since the value is known at every timestep. Many examples I have seen use t as a parameter. Is there a recommended way on how to proceed?

[ChrisRackauckas]

Are independent variables variables or parameters? They are known, and they aren't states, so they are almost like parameters, but they aren't something the user actually sets. I am inclined to call them variables moreso than parameters, but maybe one of the things that could help would be to require it to have separate metadata saying that it's an independent variable. However, one of the things being exploited in physics-informed neural networks is "parameters as independent variables", so keeping that relationship is interesting and useful.

[JKRT]

@ChrisRackauckas This is also something that confused me initially. I view the DAE system like this:

but it seems that ModelingToolkit does not differentiate between state and algebraic variables (Disclaimer: note that I may just have confused myself somehow.. after lunch here in Sweden).
For instance

using ModelingToolkit, NonlinearSolve

@variables x y z
@parameters σ ρ β

# Define a nonlinear system
eqs = [0 ~ σ*(y-x),
       0 ~ x*(ρ-z)-y,
       0 ~ x*y - β*z]
ns = NonlinearSystem(eqs, [x,y,z], [σ,ρ,β])

Results in:

Model ##NonlinearSystem#3546 with 3 equations
States (3):
  x
  y
  z
Parameters (3):
  σ
  ρ
  β

For instance, in the example above all my variables that I declare to be dependent on time explicitly is the state variables (Using DAE terminology)
{
omega_1(t),
Phi_1(t),
Phi_2(t),
omega_2(t),
}

[ChrisRackauckas]

but it seems that ModelingToolkit does not differentiate between state and algebraic variables (Disclaimer: note that I may just have confused myself somehow.. after lunch here in Sweden).

Yes, and they can switch around due to structural simplifications, index reduction, etc. kinds of things.

[YingboMa]

Yes, it's MTK's responsibility to figure out what are differential equations/variables and what are algebraic equations/variables.