hyperbox-brain is a Python open source toolbox implementing hyperbox-based machine learning algorithms built on top of scikit-learn and is distributed under the GPL-3 license.
The project was started in 2018 by Prof. Bogdan Gabrys and Dr. Thanh Tung Khuat at the Complex Adaptive Systems Lab - The University of Technology Sydney. This project is a core module aiming to the formulation of explainable life-long learning systems in near future.
Table of Contents
- Resources
- Installation
- Features
- Types of input variables
- Incremental learning
- Agglomerative learning
- Ensemble learning
- Multigranularity learning
- Learning from both labelled and unlabelled data
- Ability to directly process missing data
- Continual learning of new classes in an incremental manner
- Data editing and pruning approaches
- Scikit-learn compatible estimators
- Explainability of predicted results
- Easy to use
- Jupyter notebooks
- Available models
- Examples
- Citation
- Contributing
- License
- References
Hyperbox-brain requires:
- Python (>= 3.6)
- Scikit-learn (>= 0.24.0)
- NumPy (>= 1.14.6)
- SciPy (>= 1.1.0)
- joblib (>= 0.11)
- threadpoolctl (>= 2.0.0)
- Pandas (>= 0.25.0)
Hyperbox-brain plotting capabilities (i.e., functions start with show_ or draw_)
require Matplotlib (>= 2.2.3) and Plotly (>= 4.10.0).
For running the examples Matplotlib >= 2.2.3 and Plotly >= 4.10.0 are required.
A few examples require pandas >= 0.25.0.
You need a working conda installation. Get the correct miniconda for your system from here.
To install hyperbox-brain, you need to use the conda-forge channel:
conda install -c conda-forge hyperbox-brainWe recommend to use a conda virtual environment.
If you already have a working installation of numpy, scipy, pandas, matplotlib,
and scikit-learn, the easiest way to install hyperbox-brain is using pip:
pip install -U hyperbox-brainAgain, we recommend to use a virtual environment for this.
If you would like to use the most recent additions to hyperbox-brain or help development, you should install hyperbox-brain from source.
To install hyperbox-brain from source using conda, proceed as follows:
git clone https://github.com/UTS-CASLab/hyperbox-brain.git
cd hyperbox-brain
conda env create
source activate hyperbox-brain
pip install .For pip, follow these instructions instead:
git clone https://github.com/UTS-CASLab/hyperbox-brain.git
cd hyperbox-brain
# create and activate a virtual environment
pip install -r requirements.txt
# install hyperbox-brain version for your system (see below)
pip install .After installation, you can launch the test suite from outside the source
directory (you will need to have pytest >= 5.0.1 installed):
pytest hbbrainThe hyperbox-brain library separates learning models for continuous variables only and mixed-attribute data.
Incremental (online) learning models are created incrementally and are updated continuously. They are appropriate for big data applications where real-time response is an important requirement. These learning models generate a new hyperbox or expand an existing hyperbox to cover each incoming input pattern.
Agglomerative (batch) learning models are trained using all training data available at the training time. They use the aggregation of existing hyperboxes to form new larger sized hyperboxes based on the similarity measures among hyperboxes.
Ensemble models in the hyperbox-brain toolbox build a set of hyperbox-based learners from a subset of training samples or a subset of both training samples and features. Training subsets of base learners can be formed by stratified random subsampling, resampling, or class-balanced random subsampling. The final predicted results of an ensemble model are an aggregation of predictions from all base learners based on a majority voting mechanism. An intersting characteristic of hyperbox-based models is resulting hyperboxes from all base learners or decision trees can be merged to formulate a single model. This contributes to increasing the explainability of the estimator while still taking advantage of strong points of ensemble models.
Multi-granularity learning algorithms can construct classifiers from multiresolution hierarchical granular representations using hyperbox fuzzy sets. This algorithm forms a series of granular inferences hierarchically through many levels of abstraction. An attractive characteristic of these classifiers is that they can maintain a high accuracy in comparison to other fuzzy min-max models at a low degree of granularity based on reusing the knowledge learned from lower levels of abstraction.
One of the exciting features of learning algorithms for the general fuzzy min-max neural network is the capability of creating classification boundaries among known classes and clustering data and representing them as hyperboxes in the case that labels are not available. Unlabelled hyperboxes is then possible to be labelled on the basis of the evidence of next incoming input samples. As a result, the GFMMNN models have the ability to learn from the mixed labelled and unlabelled datasets in a native way.
Learning algorithms for the general fuzzy min-max neural network supported by the library may classify inputs with missing data directly without the need for replacing or imputing missing values as in other classifiers.
Incremental learning algorithms of hyperbox-based models in the hyperbox-brain library can grow and accommodate new classes of data without retraining the whole classifier. Incremental learning algorithms themselves can generate new hyperboxes to represent clusters of new data with potentially new class labels both in the middle of normal training procedure and in the operating time where training has been finished. This property is a key feature for smart life-long learning systems.
By combining the repeated cross-validation methods provided by scikit-learn and hyperbox-based learning algorithms, evidence from training multiple models can be deployed for identifying which data points from the original training set or the hyperboxes from the generated multiple models should be retained and those that should be edited out or pruned before further processing.
The estimators in hyperbox-brain is compatible with the well-known scikit-learn toolbox. Therefore, it is possible to use hyperbox-based estimators in scikit-learn pipelines, scikit-learn hyperparameter optimizers (e.g., grid search and random search), and scikit-learn model validation (e.g., cross-validation scores). In addition, the hyperbox-brain toolbox can be used within hyperparameter optimisation libraries built on top of scikit-learn such as hyperopt.
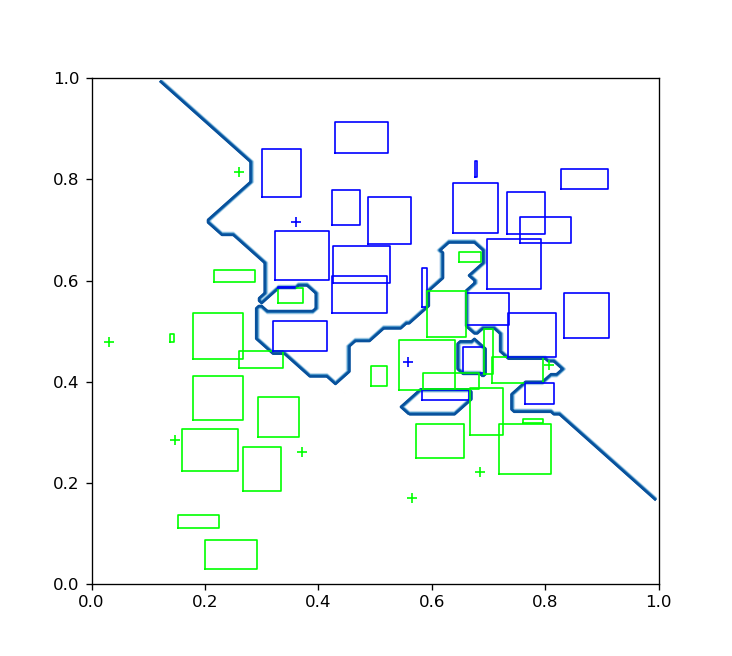
The hyperbox-brain library can provide the explanation of predicted results via visualisation. This toolbox provides the visualisation of existing hyperboxes and the decision boundaries of a trained hyperbox-based model if input features are two-dimensional features:
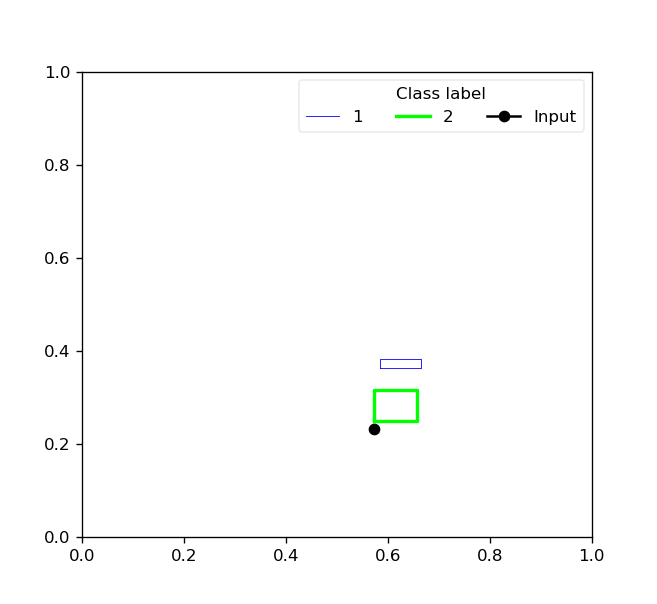
For two-dimensional data, the toolbox also provides the reason behind the class prediction for each input sample by showing representative hyperboxes for each class which join the prediction process of the trained model for an given input pattern:
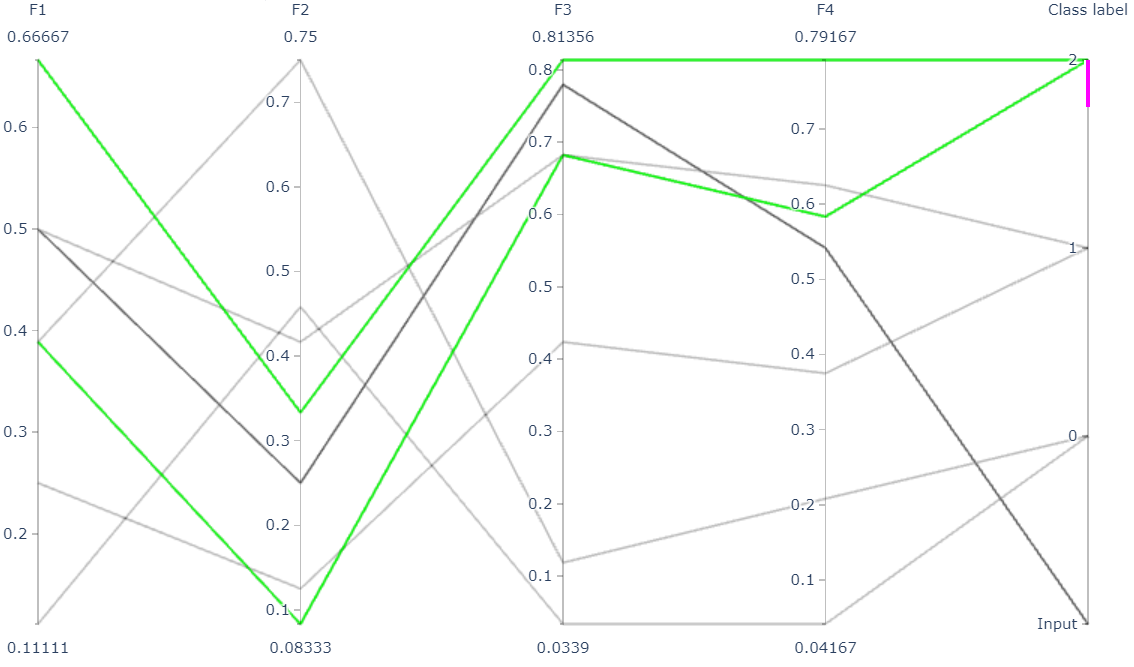
For input patterns with two or more dimensions, the hyperbox-brain toolbox uses a parallel coordinates graph to display representative hyperboxes for each class which join the prediction process of the trained model for an given input pattern:
Hyperbox-brain is designed for users with any experience level. Learning models are easy to create, setup, and run. Existing methods are easy to modify and extend.
The learning models in the hyperbox-brain toolbox can be easily retrieved in notebooks in the Jupyter or JupyterLab environments.
In order to display plots from hyperbox-brain within a Jupyter Notebook we need to define the proper mathplotlib backend to use. This can be performed by including the following magic command at the beginning of the Notebook:
%matplotlib notebookJupyterLab is the next-generation user interface for Jupyter, and it may display interactive plots with some caveats. If you use JupyterLab then the current solution is to use the jupyter-matplotlib extension:
%matplotlib widgetExamples regarding how to use the classes and functions in the hyperbox-brain toolbox have been written under the form of Jupyter notebooks.
The following table summarises the supported hyperbox-based learning algorithms in this toolbox.
| Model | Feature type | Model type | Learning type | Implementation | Example | References |
|---|---|---|---|---|---|---|
| EIOL-GFMM | Mixed | Single | Instance-incremental | ExtendedImprovedOnlineGFMM | Notebook 1 | [1] |
| Freq-Cat-Onln-GFMM | Mixed | Single | Batch-incremental | FreqCatOnlineGFMM | Notebook 2 | [2] |
| OneHot-Onln-GFMM | Mixed | Single | Batch-incremental | OneHotOnlineGFMM | Notebook 3 | [2] |
| Onln-GFMM | Continuous | Single | Instance-incremental | OnlineGFMM | Notebook 4 | [3], [4] |
| IOL-GFMM | Continuous | Single | Instance-incremental | ImprovedOnlineGFMM | Notebook 5 | [5], [4] |
| FMNN | Continuous | Single | Instance-incremental | FMNNClassifier | Notebook 6 | [6] |
| EFMNN | Continuous | Single | Instance-incremental | EFMNNClassifier | Notebook 7 | [7] |
| KNEFMNN | Continuous | Single | Instance-incremental | KNEFMNNClassifier | Notebook 8 | [8] |
| RFMNN | Continuous | Single | Instance-incremental | RFMNNClassifier | Notebook 9 | [9] |
| AGGLO-SM | Continuous | Single | Batch | AgglomerativeLearningGFMM | Notebook 10 | [10], [4] |
| AGGLO-2 | Continuous | Single | Batch | AccelAgglomerativeLearningGFMM | Notebook 11 | [10], [4] |
| MRHGRC | Continuous | Granularity | Multi-Granular learning | MultiGranularGFMM | Notebook 12 | [11] |
| Decision-level Bagging of hyperbox-based learners | Continuous | Combination | Ensemble | DecisionCombinationBagging | Notebook 13 | [12] |
| Decision-level Bagging of hyperbox-based learners with hyper-parameter optimisation | Continuous | Combination | Ensemble | DecisionCombinationCrossValBagging | Notebook 14 | |
| Model-level Bagging of hyperbox-based learners | Continuous | Combination | Ensemble | ModelCombinationBagging | Notebook 15 | [12] |
| Model-level Bagging of hyperbox-based learners with hyper-parameter optimisation | Continuous | Combination | Ensemble | ModelCombinationCrossValBagging | Notebook 16 | |
| Random hyperboxes | Continuous | Combination | Ensemble | RandomHyperboxesClassifier | Notebook 17 | [13] |
| Random hyperboxes with hyper-parameter optimisation for base learners | Continuous | Combination | Ensemble | CrossValRandomHyperboxesClassifier | Notebook 18 |
To see more elaborate examples, look here.
Simply use an estimator by initialising, fitting and predicting:
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from hbbrain.numerical_data.incremental_learner.onln_gfmm import OnlineGFMM
# Load dataset
X, y = load_iris(return_X_y=True)
# Normalise features into the range of [0, 1] because hyperbox-based models only work in a unit range
scaler = MinMaxScaler()
scaler.fit(X)
X = scaler.transform(X)
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Training a model
clf = OnlineGFMM(theta=0.1).fit(X_train, y_train)
# Make prediction
y_pred = clf.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f'Accuracy = {acc * 100: .2f}%')Using hyperbox-based estimators in a sklearn Pipeline:
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from hbbrain.numerical_data.incremental_learner.onln_gfmm import OnlineGFMM
# Load dataset
X, y = load_iris(return_X_y=True)
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Create a GFMM model
onln_gfmm_clf = OnlineGFMM(theta=0.1)
# Create a pipeline
pipe = Pipeline([
('scaler', MinMaxScaler()),
('onln_gfmm', onln_gfmm_clf)
])
# Training
pipe.fit(X_train, y_train)
# Make prediction
acc = pipe.score(X_test, y_test)
print(f'Testing accuracy = {acc * 100: .2f}%')Using hyperbox-based models with random search:
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import accuracy_score
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import train_test_split
from hbbrain.numerical_data.ensemble_learner.random_hyperboxes import RandomHyperboxesClassifier
from hbbrain.numerical_data.incremental_learner.onln_gfmm import OnlineGFMM
# Load dataset
X, y = load_breast_cancer(return_X_y=True)
# Normalise features into the range of [0, 1] because hyperbox-based models only work in a unit range
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Initialise search ranges for hyper-parameters
parameters = {'n_estimators': [20, 30, 50, 100, 200, 500],
'max_samples': [0.2, 0.3, 0.4, 0.5, 0.6],
'max_features' : [0.2, 0.3, 0.4, 0.5, 0.6],
'class_balanced' : [True, False],
'feature_balanced' : [True, False],
'n_jobs' : [4],
'random_state' : [0],
'base_estimator__theta' : np.arange(0.05, 0.61, 0.05),
'base_estimator__gamma' : [0.5, 1, 2, 4, 8, 16]}
# Init base learner. This example uses the original online learning algorithm to train a GFMM classifier
base_estimator = OnlineGFMM()
# Using random search with only 40 random combinations of parameters
random_hyperboxes_clf = RandomHyperboxesClassifier(base_estimator=base_estimator)
clf_rd_search = RandomizedSearchCV(random_hyperboxes_clf, parameters, n_iter=40, cv=5, random_state=0)
# Fit model
clf_rd_search.fit(X_train, y_train)
# Print out best scores and hyper-parameters
print("Best average score = ", clf_rd_search.best_score_)
print("Best params: ", clf_rd_search.best_params_)
# Using the best model to make prediction
best_gfmm_rd_search = clf_rd_search.best_estimator_
y_pred_rd_search = best_gfmm_rd_search.predict(X_test)
acc_rd_search = accuracy_score(y_test, y_pred_rd_search)
print(f'Accuracy (random-search) = {acc_rd_search * 100: .2f}%')If you use hyperbox-brain in a scientific publication, we would appreciate citations to the following paper:
@article{khga23,
title={hyperbox-brain: A Python toolbox for hyperbox-based machine learning algorithms},
author={Khuat, Thanh Tung and Gabrys, Bogdan},
journal={SoftwareX},
volume={23},
pages={101425},
year={2023},
url={https://doi.org/10.1016/j.softx.2023.101425},
publisher={Elsevier}
}
Feel free to contribute in any way you like, we're always open to new ideas and approaches.
There are some ways for users to get involved:
- Issue tracker: this place is meant to report bugs, request for minor features, or small improvements. Issues should be short-lived and solved as fast as possible.
- Discussions: in this place, you can ask for new features, submit your questions and get help, propose new ideas, or even show the community what you are achieving with hyperbox-brain! If you have a new algorithm or want to port a new functionality to hyperbox-brain, this is the place to discuss.
- Contributing guide: in this place, you can learn more about making a contribution to the hyperbox-brain toolbox.
Hyperbox-brain is free and open-source software licensed under the GNU General Public License v3.0.
| [1] | : T. T. Khuat and B. Gabrys "An Online Learning Algorithm for a Neuro-Fuzzy Classifier with Mixed-Attribute Data", ArXiv preprint, arXiv:2009.14670, 2020. |
| [2] | (1, 2) : T. T. Khuat and B. Gabrys "An in-depth comparison of methods handling mixed-attribute data for general fuzzy min–max neural network", Neurocomputing, vol 464, pp. 175-202, 2021. |
| [3] | : B. Gabrys and A. Bargiela, "General fuzzy min-max neural network for clustering and classification", IEEE Transactions on Neural Networks, vol. 11, no. 3, pp. 769-783, 2000. |
| [4] | (1, 2, 3, 4) : T. T. Khuat and B. Gabrys, "Accelerated learning algorithms of general fuzzy min-max neural network using a novel hyperbox selection rule", Information Sciences, vol. 547, pp. 887-909, 2021. |
| [5] | : T. T. Khuat, F. Chen, and B. Gabrys, "An improved online learning algorithm for general fuzzy min-max neural network", in Proceedings of the International Joint Conference on Neural Networks (IJCNN), pp. 1-9, 2020. |
| [6] | : P. Simpson, "Fuzzy min—max neural networks—Part 1: Classification", IEEE Transactions on Neural Networks, vol. 3, no. 5, pp. 776-786, 1992. |
| [7] | : M. Mohammed and C. P. Lim, "An enhanced fuzzy min-max neural network for pattern classification", IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 3, pp. 417-429, 2014. |
| [8] | : M. Mohammed and C. P. Lim, "Improving the Fuzzy Min-Max neural network with a k-nearest hyperbox expansion rule for pattern classification", Applied Soft Computing, vol. 52, pp. 135-145, 2017. |
| [9] | : O. N. Al-Sayaydeh, M. F. Mohammed, E. Alhroob, H. Tao, and C. P. Lim, "A refined fuzzy min-max neural network with new learning procedures for pattern classification", IEEE Transactions on Fuzzy Systems, vol. 28, no. 10, pp. 2480-2494, 2019. |
| [10] | (1, 2) : B. Gabrys, "Agglomerative learning algorithms for general fuzzy min-max neural network", Journal of VLSI Signal Processing Systems for Signal, Image and Video Technology, vol. 32, no. 1, pp. 67-82, 2002. |
| [11] | : T.T. Khuat, F. Chen, and B. Gabrys, "An Effective Multiresolution Hierarchical Granular Representation Based Classifier Using General Fuzzy Min-Max Neural Network", IEEE Transactions on Fuzzy Systems, vol. 29, no. 2, pp. 427-441, 2021. |
| [12] | (1, 2) : B. Gabrys, "Combining neuro-fuzzy classifiers for improved generalisation and reliability", in Proceedings of the 2002 International Joint Conference on Neural Networks, vol. 3, pp. 2410-2415, 2002. |
| [13] | : T. T. Khuat and B. Gabrys, "Random Hyperboxes", IEEE Transactions on Neural Networks and Learning Systems, 2021. |