Skip to content

UtopianFuture/leetcode

BranchesTags

Folders and files

NameName
Last commit message
Last commit date

Latest commit

 

History

435 Commits
.husky
.husky
 
 
image
image
 
 
script/hook
script/hook
 
 
.lintmdrc.json
.lintmdrc.json
 
 
.pre-commit-config.yaml
.pre-commit-config.yaml
 
 
CBTInserter.cpp
CBTInserter.cpp
 
 
LRUCache.c
LRUCache.c
 
 
LRUCache.cpp
LRUCache.cpp
 
 
PredictTheWinner.cpp
PredictTheWinner.cpp
 
 
README.md
README.md
 
 
add.cpp
add.cpp
 
 
addBinary.cpp
addBinary.cpp
 
 
addTwoNumbers.cpp
addTwoNumbers.cpp
 
 
addTwoNumbers_ii.cpp
addTwoNumbers_ii.cpp
 
 
advantageCount.cpp
advantageCount.cpp
 
 
allPathsSourceTarget.cpp
allPathsSourceTarget.cpp
 
 
arrayNesting.cpp
arrayNesting.cpp
 
 
asteroidCollision.cpp
asteroidCollision.cpp
 
 
averageOfLevels.cpp
averageOfLevels.cpp
 
 
buildTree.c
buildTree.c
 
 
buildTree.h
buildTree.h
 
 
buildTree_ii.cpp
buildTree_ii.cpp
 
 
bulbSwitch.cpp
bulbSwitch.cpp
 
 
calculate.cpp
calculate.cpp
 
 
calculateMinimumHP.cpp
calculateMinimumHP.cpp
 
 
canCompleteCircuit.cpp
canCompleteCircuit.cpp
 
 
canFinish.cpp
canFinish.cpp
 
 
canIWin.cpp
canIWin.cpp
 
 
canJump.cpp
canJump.cpp
 
 
canPartition.cpp
canPartition.cpp
 
 
canPartitionKSubsets.cpp
canPartitionKSubsets.cpp
 
 
canWinNim.cpp
canWinNim.cpp
 
 
carPooling.cpp
carPooling.cpp
 
 
change.cpp
change.cpp
 
 
checkInclusion.cpp
checkInclusion.cpp
 
 
checkSubarraySum.cpp
checkSubarraySum.cpp
 
 
climbStairs.c
climbStairs.c
 
 
closedIsland.cpp
closedIsland.cpp
 
 
coinchange.c
coinchange.c
 
 
combinationSum.cpp
combinationSum.cpp
 
 
combinationSum_ii.cpp
combinationSum_ii.cpp
 
 
combinationSum_iii.cpp
combinationSum_iii.cpp
 
 
combinationSum_iv.cpp
combinationSum_iv.cpp
 
 
combine.cpp
combine.cpp
 
 
compareVersion.cpp
compareVersion.cpp
 
 
compress.cpp
compress.cpp
 
 
connect.cpp
connect.cpp
 
 
connect_ii.cpp
connect_ii.cpp
 
 
consecutiveNumbersSum.cpp
consecutiveNumbersSum.cpp
 
 
constrainedSubsetSum.cpp
constrainedSubsetSum.cpp
 
 
constructArr.cpp
constructArr.cpp
 
 
constructMaximumBinaryTree.cpp
constructMaximumBinaryTree.cpp
 
 
convert.cpp
convert.cpp
 
 
convertBST.cpp
convertBST.cpp
 
 
copyRandomList.cpp
copyRandomList.cpp
 
 
corpFlightBookings.cpp
corpFlightBookings.cpp
 
 
countAndSay.cpp
countAndSay.cpp
 
 
countBits.cpp
countBits.cpp
 
 
countDigitOne.cpp
countDigitOne.cpp
 
 
countNodes.cpp
countNodes.cpp
 
 
countPrimes.cpp
countPrimes.cpp
 
 
countRangeSum.cpp
countRangeSum.cpp
 
 
countSubIslands.cpp
countSubIslands.cpp
 
 
countSubstrings.cpp
countSubstrings.cpp
 
 
cuttingRope.cpp
cuttingRope.cpp
 
 
dailyTemperatures.cpp
dailyTemperatures.cpp
 
 
decodeString.cpp
decodeString.cpp
 
 
deleteAndEarn.c
deleteAndEarn.c
 
 
deleteNode.c
deleteNode.c
 
 
designTwitter.c
designTwitter.c
 
 
detectCycle.cpp
detectCycle.cpp
 
 
diameterOfBinaryTree.cpp
diameterOfBinaryTree.cpp
 
 
diffWaysToCompute.cpp
diffWaysToCompute.cpp
 
 
distanceK.cpp
distanceK.cpp
 
 
eliminateMaximum.cpp
eliminateMaximum.cpp
 
 
equalSubstring.cpp
equalSubstring.cpp
 
 
equationsPossible.cpp
equationsPossible.cpp
 
 
eraseOverlapIntervals.c
eraseOverlapIntervals.c
 
 
eraseOverlapIntervals.cpp
eraseOverlapIntervals.cpp
 
 
evalRPN.cpp
evalRPN.cpp
 
 
examRoom.cpp
examRoom.cpp
 
 
exchange.cpp
exchange.cpp
 
 
fib.c
fib.c
 
 
findAnagrams.cpp
findAnagrams.cpp
 
 
findBall.cpp
findBall.cpp
 
 
findBottomLeftValue.cpp
findBottomLeftValue.cpp
 
 
findCheapestPrice.cpp
findCheapestPrice.cpp
 
 
findClosestElements.cpp
findClosestElements.cpp
 
 
findContinuousSequence.cpp
findContinuousSequence.cpp
 
 
findDisappearedNumbers.cpp
findDisappearedNumbers.cpp
 
 
findDuplicate.cpp
findDuplicate.cpp
 
 
findDuplicateSubtrees.cpp
findDuplicateSubtrees.cpp
 
 
findDuplicates.cpp
findDuplicates.cpp
 
 
findErrorNums.cpp
findErrorNums.cpp
 
 
findKthLargest.cpp
findKthLargest.cpp
 
 
findLength.cpp
findLength.cpp
 
 
findLongestWord.cpp
findLongestWord.cpp
 
 
findMaxLength.cpp
findMaxLength.cpp
 
 
findMedian.cpp
findMedian.cpp
 
 
findMinArrowShots.c
findMinArrowShots.c
 
 

Repository files navigation

leetcode

重要思想

  • 二叉树解题的思维模式分两类：

    • 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

    • 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

  • 二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

题目

  1. fib 这题动态规划解法和递归解法的区别是消除重复子问题。

  2. coinChange 最重要的是理解 dp，dp 是一个数组，长度为 amount + 1(0 ~ amount)，每个元素表示该 amount 最少的分配方式，除 dp[0] = 0 外，其他的元素都初始化为 amount + 1，即默认是没有正确的分配方式。另一个关键是理解 amount 的最少分配方式是 amount - coins[i] 的最少分配方式加 1。

    dp[i] = (dp[i] < (dp[i - coins[j]] + 1)) ? dp[i] : (dp[i - coins[j]] + 1);

  3. change

    和上一题不一样，这题是 0-1 背包问题，dp[i][j] 表示若只使用前 i 个物品（可以重复使用），当背包容量为 j 时，有 dp[i][j] 种方法可以装满背包。然后考虑 2 中情况：

    • 如果你不把这第 i 个物品装入背包，也就是说你不使用 coins[i] 这个面值的硬币，那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j]，继承之前的结果。

    • 如果你把这第 i 个物品装入了背包，也就是说你使用 coins[i] 这个面值的硬币，那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。

  4. climbStairs 最后一次可能是跨一步或两步，即：

    dp[i] = dp[i - 1] + dp[i - 2];

  5. mincostTickets 这题大体上和 coinchange 一样，但有一点需要注意，由于天数不是连续的，所有没有去旅游的那天 cost 和前一天一样。

    if (dp[i] != 0) {
  dp[i] = dp[i] < dp[i - tickets[j]] + 1 ? dp[i] : dp[i - tickets[j]] + 1;
} else {
  dp[i] = dp[i - 1];
}

  6. lengthOfLIS LIS: 最长递增自序列 思路和 coinchange 一样，即：LIS 等于前面的比自己小的元素中的 LIS 加 1。

  7. minDistance 还是动态规划，思路是最短距离等于上 word1[size1] ~ word2[size2 - 1] 的最短距离加 1。但这题的 dp 是二维数组，dp[i][j] 表示 word1[i] 到 word2[j] 的最短距离。然后关于增，删和替换操作体现在 dp 上就是:

      x h o r s e
x 0 1 2 3 4 5
r 1
o 2
s 3

    当 i = 1, j = 1 时 dp[i - 1][j]; // 删除 h dp[i][j - 1]; // 在 r 前面增加 h dp[i - 1][j - 1]; // 替换

  8. minimumDeleteSum 思路和上一题基本一致，有几个关键点:

  • dp 数组是二维的，
  • dp base 是 val[0][i] = val[0][i - 1] + s2[i - 1];
  • 状态转移方程为 min = {(val[i - 1][j] + s1[i - 1]), (val[i][j - 1] + s2[j - 1])}
  • dp 数组一定要先初始化再使用，不然会出现在本地机器上正常执行而 leetcode 的编译器上返回未初始化的值， 这应该是编译器的问题，本地的编译器将这个隐藏的 bug 优化了。

  1. superEggDrop 在使用二分查找优化时遇到困难，我想不用递归的方式优化，但是无法实现。

    首先确定状态转移方程：

    dp[i][j] 表示 i 个鸡蛋，j 层楼最多需要扔几次。那么有 kn 种情况，然后要测出每种情况在最坏情况下需要测几次，我们可以遍历 i - 1 层楼，找出最好的情况。举个例子，当 k = 2, n = 9 时，我们在 5 楼测一次，那么 dp[2][9] = max(dp[1][4], dp[2][4]) + 1，但是这种方法的时间复杂度为 kn^2，很多案例不能通过。 我们也可以换种思路，题目的要求为 k 个鸡蛋，n 层楼，最坏情况下最少的测试次数 m，我们可以转换成 k 个鸡蛋，测试 m 次，最坏情况下最多能测试 n 层楼，即 dp[i][j] 表示 n 层楼，当 dp[i][i] == n 时的 m 即为所求。dp base 为 dp[1][i] = 1;， 状态转换方程为：

    dp[i][j] = 1 + dp[i - 1][j - 1] + dp[i - 1][j];

    i 表示测试次数，j 表示鸡蛋数。

  2. longestPalindromeSubseq 这题的思路是这样的：dp[i][j] 表示 s[i ~ j] 子序列的最长回文子序列，对于任一个子序列的 s[i], s[j] 都有两种情况：

  • s[i] = s[j] 那么 s[i], s[j] 就可以加入到最长回文子序列中

    dp[i][j] = dp[i + 1][j - 1] + 2;

  • s[i] != s[j]

    那 s[i], s[j] 就不能作为最长回文子序列首尾

    dp[i][j] = dp[i + 1][j] > dp[i][j - 1] ? dp[i + 1][j] : dp[i][j - 1];

  1. stoneGame dp[i][j] 表示 piles[i ~ j] 石子堆中当前玩家与另一个玩家的石子数量差的最大值， dp base 是 dp[i][i] = piles[i]，要求的是 dp[0][size]， 当 i < j 时，当前玩家可以选择取走 piles[i] 或 piles[j]， 然后轮到另一个玩家在剩下的石子堆中取走石子。在两种方案中，当前玩家会选择最优的方案，使得自己的石子数量最大化。而状态转移方程为：

    dp[i][j] = max{piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]}

    官方解析中给出了数学分析，这种情况永远是先手获胜，所以可以直接返回 true。总结一下这题和上一题，虽然给出的都是一个序列，但是 dp 数组都是二维的，因为需要遍历这个序列中每个字符的每种组合。然后关于状态转移方程，应该先考虑将问题分为子问题，如这题分成 piles[i ~ j] 子序列，上题也是分成 s[i ~ j] 子序列。分成子问题之后再考虑怎样转移，那么就要确定最终要求什么，如上题要求最长回文子序列的长度，那么子问题就也是求长度，加上新的字符长度会怎样变化，这题需要将胜负转换成差值，然后求差值。

  2. eraseOverlapIntervals 首先这题的代码在 leetcode 上能通过，但是在本地编译错误，应该是使用的 qsort 不同。这题是区间调度的题目，思路和之前的动态规划有很大不同，将它归为单纯的贪心比较合适。将 intervals 按 end 递增序排列，不重叠要满足条件 intervals[i][0] >= base[1] ，即 end >= start，将不满足条件的 intervals[i] 去掉即可。

  3. findMinArrowShots 这题和上一题一样。

  4. strStr 这题用暴力解法法超时，需要使用 kmp 算法。使用 kmp 算法解决字符匹配类问题的关键就是 pat 字符串的 kmp 数组。然后根据 kmp 数组求解。每个字符串对应的 kmp 数组是确定的，可以用这个算法来求:

    int pi[size2];
pi[0] = 0;
for (int i = 1, j = 0; i < size2; i++) {
  while (j > 0 && needle[i] != needle[j]) {
    j = pi[j - 1];
  }
  if (needle[i] == needle[j]) {
    j++;
  }
  pi[i] = j;
}

    然后确定 pat 字符串是否在 txt 字符串中出现过，可以使用这个算法:

    for (int i = 0, j = 0; i < size1; i++) {
  while (j > 0 && haystack[i] != needle[j]) {
    j = pi[j - 1];
  }
  if (haystack[i] == needle[j]) {
    j++;
  }
  if (j == size2) {
    return i - size2 + 1;
  }
}

  5. repeatedSubstringPattern 这题也是用 kmp 算法，但是比较巧妙，给定一个非空的字符串，判断它是否可以由它的一个子串重复多次构成。将这个字符串重复两次，变成 s[0 ~ 2 * size - 1]， 如果这个字符串可以由它的一个子串重复多次构成，那么在 s[1 ~ 2 * size -2] 中一定存在该子串。

  6. shortestPalindrome 这题的做法很巧妙，求最短回文串，用暴力的解法比较简单，将后面的字符和前面的字符一个个遍历对比，如果不相同，则插入。而 KMP 算法是先求出原字符串的 next 数组，然后将字符串反转得到 txt 数组。之后按照 kmp 遍历，看 txt 数组的最后一个字符对应 next 数组的哪个字符，将该字符之后的字符都加入到 txt 数组。

    暴力算法最后两个案例不能通过。

  7. longestPalindrome

  • 原做法（错误） 这题没有使用 kmp 算法，而是使用动态规划，dp[i][j] 表示 s[i ~ j] 的最长回文串， 注意这里还需要考虑一个事情

    if (s[i] == s[j] && ((dp[i + 1][j] >= j - i - 1) || (dp[i][j - 1] >= j - i - 1)))

    即当 s[i] == s[j] 时还要看 s[i + 1 ~ j] 和 s[i ~ j - 1] 是否是回文串。 如果不考虑会出现这种情况: asdfa 最后一个字符和第一个字符相等，但是中间的三个字符不是回文串，所以不能直接加 2。

  • 新做法 不要想的那么复杂，考虑两点: （1）遍历每一个子串， （2）动态转移方程 动态转移方程是这样的: （1）dp 数组表示 s[i] ~ s[j] 是否是回文串； （1）如果该子串 s[i] != s[j]， 那么这个子串肯定不是回文； （2）如果 s[i] == s[j]，那么该子串是否是回文跟 s[i + 1] ~ s[j - 1] 相同。 这题和 9. 最长回文子序列 需要分清楚，一个是子序列，可以不连续，dp 数组表示的是 s[i ~ j] 子串中的最长回文子序列长度，而这题 dp 数组表示的 s[i ~ j] 是否是回文子串。动态转移方程是是类似的。

        char *res = malloc((max + 1) * sizeof(char));
     for (int i = 0; i < max; i++) {
       res[res_size++] = s[i + low];
     }
     res[res_size] = 0;

    还有一点需要注意，由于使用了 -fsanitize=address 来进行边界检查，所以在创建 char * 时要这样，即数组大小比需要的大 1，然后最后一个 byte 设为 0。

    原来这题是逐个遍历长度，而不是用一般的遍历 i, j 的方法。

  1. maxProfit 股票问题： 这种问题有 3 个状态，天数，允许交易的最大次数和当前是否持有股票。利用三维 dp 数组可以表示所有的状态：

    dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数，大 K 为交易数的上限，0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
  for 1 <= k <= K:
      for s in {0, 1}:
          dp[i][k][s] = max(buy, sell, rest)

    然后最后要求的就是 dp[n - 1][K][0] 那么状态转移方程是这样的：

    // 今天没有持有股票，可能是保持昨天的状态，也可能是昨天持有股票，但是今天卖了
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
// 今天持有股票，可能是保持昨天的状态，也可能是今天买入股票，那么最大交易次数就减 1。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

    最后的代码是这样的，

      int maxProfit(vector<int> &prices) {
    int n = (int)prices.size();
    if (n == 0) {
      return 0;
    }
    vector<int> dp_0(n, 0);
    vector<int> dp_1(n, 0);
    // dp base
    dp_0[0] = 0;          // the first day don't have stock, so the profit is 0.
    dp_1[0] = -prices[0]; // the first day should not have any stock, so the
                          // profit is -prices[0].
    for (int i = 1; i < n; i++) {
      dp_0[i] = max(dp_0[i - 1], dp_1[i - 1] + prices[i]);
      // 这里不用 dp_0[i - 1] - prices[i] 是因为 k = 1
      // 而 k = 0 是 base case，所以 dp[i-1][0][0] = 0。
      dp_1[i] = max(dp_1[i - 1], -prices[i]);
    }
    return dp_0[n - 1];
  }

  2. maxProfit_ii dp base 还是和上题一样

    int dp_0 = 0, dp_1 = 0x80000001;

    状态转移方程也是一样的，

    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

    但是 k 是无限的，[k] 和 [k - 1] 一样，可以约掉， 得到如下状态转移方程，

    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

    那么 k 成为无关状态，

    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])

    再将 dp[i][0] 化简为 dp_0，这里有一点需要注意，dp[i][0] 表示的是上一天的利润， 换成 dp_0 后

    dp_0 = max(dp_0, dp_1 + prices[i]);
dp_1 = max(dp_1, dp_0 - prices[i]);

    dp_0 已经经过计算，变成今天的利润，所以要利用一个 temp 来记录昨天的利润。

  3. maxProfit_iii 这题是上一题的进一步，k = 2，之后类似的题目都是套这种模板，

  • dp base 
    for (int i = 0; i < pricesSize; i++) {
  dp_0[i][0] = 0;
  dp_1[i][0] = -prices[i];
}
    dp base 都是第 0 天的时候手中有股票 dp_0 初始化为 0，手中没有股票 dp_1 初始化为 -prices[0]。

  1. maxProfit_iv k = integer，但是如果 k > days / 2 的就和 k = inf 一样的， 所以在上一题的基础加上加一个限制条件即可

    if (k > pricesSize / 2) {
  return maxProfit_inf(prices, pricesSize);
}

  2. maxProfit_freeze 这题在 18 题的基础上简单修改一下即可，冰冻期为 n 则状态转移方程变为：

    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-n][k][0] - prices[i])

    然后一样，k 变成无关变量，可以约掉。

  3. maxProfit_fee 这题还是 18 题的变种，只需要在收入上减去 fee 即可。

    dp_0 = dp_0 > dp_1 + prices[i] - fee ? dp_0 : dp_1 + prices[i] - fee;

  4. rob 这题比较简单，用一个一维的 dp 数组表示到当前房间时最高金额。

  • dp base

    if(numsSize == 1){
  return nums[0];
}
if(numsSize == 2){
  return nums[0] > nums[1] ? nums[0] : nums[1];
}
if(numsSize == 3){
  return nums[0] + nums[2] > nums[1] ? nums[0] + nums[2] : nums[1];
}

dp[0] = nums[0];
dp[1] = nums[1];
dp[2] = nums[2] + dp[0];

  • 状态转移方程

    dp[i] = max(dp[i - 2], dp[i - 3]) + nums[i]

    但其实这个状态转移方程更容易理解，

    dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

  1. rob_ii 首尾是连接的，那么就分两种情况考虑， （1）抢劫 first house 不抢劫 last house

    dp[0] = nums[0];
dp[1] = nums[1];
dp[2] = nums[2] + dp[0];
for (int i = 3; i < numsSize - 1; i++) { // don't rob the last house
  dp[i] = dp[i - 2] > dp[i - 3] ? dp[i - 2] + nums[i] : dp[i - 3] + nums[i];
}

    （2）抢劫 last house 不抢劫 first house

    dp[1] = nums[1];
dp[2] = nums[2];
dp[3] = nums[3] + dp[1];
for (int i = 4; i < numsSize; i++) { // don't rob the first house
  dp[i] = 0;
  dp[i] = dp[i - 2] > dp[i - 3] ? dp[i - 2] + nums[i] : dp[i - 3] + nums[i];
}

    返回大的那个。

  2. rob_iii 这题虽然用的也是和上题类似的动态规划思路，但由于需要遍历的是二插树，又有些不一样。每个节点可能被抢也可能没被抢，定义一个结构体来表示每个节点的状态，

    struct status {
int do_rob; // 该 house 被抢劫后的总金额
int dont_rob; // 该 house 没被抢劫的总金额
};

    遍历每个节点，

    struct status left = dp(node->left);
struct status right = dp(node->right);

    而该节点的状态是这样的，

    // 如果该节点被抢劫，那么总金额为该节点的金额加上子结点没有被抢劫的金额
int do_rob = node->val + left.dont_rob + right.dont_rob;
// 如果该节点没有被抢劫，那么子结点可被抢也可不被抢，总金额为大的那个
int dont_rob =
    (left.do_rob > left.dont_rob ? left.do_rob : left.dont_rob) +
    (right.do_rob > right.dont_rob ? right.do_rob : right.dont_rob);

    这题根据二叉树的分解问题的思路可以写出更好理解的代码，

    private:
  unordered_map<TreeNode *, int> visited;

public:
  int rob(TreeNode *root) {
    if (!root) {
      return 0;
    }

    if (visited[root]) {
      return visited[root];
    }

    int isrob = // 抢这个节点
        root->val +
        (root->left != NULL ? rob(root->left->left) + rob(root->left->right)
                            : 0) +
        (root->right != NULL ? rob(root->right->left) + rob(root->right->right)
                             : 0);
    int notrob = rob(root->left) + rob(root->right); // 不抢这个节点
    int res = max(isrob, notrob);
    visited[root] = res;
    return res;
  }

  3. isMatch_regular 这题开始想错了方向，想着直接使用 kmp 字符匹配，然后对 '.', '*' 进行特殊处理即可，例如：

    if ((p[i] == '*' && (p[i - 1] == s[j] || p[i - 1] == '.')) ||
  p[i] == s[j] || p[i] == '.') {
  j++;
}

    但是没有抓住问题的关键，即 '*' 的匹配的次数，可以为任意次。那么当 p[i + 1] == '*' 时，我们遍历所有的情况，即匹配 0 次或多次。

    if (p[j + 1] == '*') {
    // "j + 2" - '*' match 0 time, "i + 1" - '*' match 1 time
    // dp(s, i + 1, p, j) can match many times
    res = dp(s, i, p, j + 2) || dp(s, i + 1, p, j);
  }

    但关键是这点想不到啊。

    还是使用 DFS，不过细节处理起来很麻烦，有些案例没有通过。

  4. isMatch_wildcard 这题和上一题一样，只是 '*' 的意义变成匹配任意字符串，那么当 p[j] == '*' 时还是匹配 0 个字符或多个字符。

    if (p[j] == '*') {
  // 'j + 1' match 0 time, 'i + 1' match 1 time
  res = dp(s, i, sizes, p, j + 1, sizep) || dp(s, i + 1, sizes, p, j, sizep);
}

    但是这个做法会超时，所以使用了参考解法，还是动态规划的思路，动态转移方程：

    if (s[j - 1] == p[i - 1] || p[i - 1] == '?') {
  dp[i][j] = dp[i - 1][j - 1];
} else if (p[i - 1] == '*') {
  dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
} else {
  dp[i][j] = 0;
}

    dp base:

    这里 dp base 比较巧妙，当两个空字符串匹配时返回 true，

    当 p[i] == '*' 时返回 true。

    int dp[sizep + 1][sizes + 1];
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for (int i = 1; i <= sizep; i++) {
  if (p[i - 1] == '*') {
    dp[i][0] = 1;
  } else {
    break;
  }
}

  5. longestCommonSubsequence 这题是比较简单的动态规划问题。看到两个字符串，条件反射的想到 dp 数组是二维的，然后状态转移方程是：

    if (text1[i - 1] == text2[j - 1]) {
  dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
  dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];

    总结一下，涉及的公共子序列，子串等的题目都是用二维 dp 数组，然后在 dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1] 中找转移方程。

  6. maxProduct 这题和之前的动态规划有些不一样，因为它不满足“最优子结构”，即当前位置的最优解未必是由前一个位置的最优解转移得到的。所以不能直接用二维 dp 数组来解决。考虑题义，nums[i] 可正可负，可能前一个子序列的乘积是负的，但是负负得正，所以动态转移方程是这样的：

    dp_max = max(dp_max * nums[i], dp_min * nums[i], nums[i]);
dp_min = min(dp_max * nums[i], dp_min * nums[i], nums[i]);

    不但记录最大值，还记录最小值。

  7. maxSubArray 这题比较简单。

  8. deleteAndEarn 这题和 [rob](#23. rob) 类似，但要做一个转换。删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素就等于不抢劫相邻房子。定义一个 sum 数组，

    for (int i = 0; i < numsSize; i++) {
  sum[nums[i]] += nums[i];
}

    即将无序的 nums 排列成有序的房子，没有的地方初始化为 0。

  9. LRUCache 这题需要用到双向链表和哈希表，双向循环链表作为 cache 保存 value，哈希表保存 key 与 value 在 cache 中位置的映射。对于 put 操作而言，如果 key 在哈希表中存在，那么只需要改变对应的 value，同时将这个 node 移到双向链表的头部；如果不存在，需要考虑 capacity 是否足够，如果 used < capacity 那么直接在链表头部插入一个 node，并将这个 node 的地址写入哈希表 key 对应的位置；否则需要将链表尾部的一个 node 删除，并创建一个 node 插入到链表头部。对于 get 操作，如果哈希表中存在，那么将对应的 node 移到链表头部；否则返回 -1 。cache 的数据结构是这样的：

    typedef struct {
  struct node *value_location[10001]; // hash table
  int used;
  int capacity;
  struct node *head, *tail; // list head node and tail node
} LRUCache;

    这里哈希表还可以优化，因为解决哈希冲突太麻烦了，所以将 key 的映射关系保存在 value_location[key]，size 就是 max(key) + 1。然后还有一个小技巧，在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，就是这里的 struct node *head, *tail; 这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

  10. isSameTree 用中序遍历遍历整棵树即可。

  11. implementStack 这题只是为了使用 stack，直接复制官方的解答。

  12. buildTree 根据前序遍历和中序遍历构造二叉树。前序遍历的第一个节点是根节点，然后在中序遍历中定位到根节点，即可知道左子树和右子树中的节点数目。这样以来，就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，之后递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置即可。

  13. deleteNode 删除节点分 3 种情况：

  • 叶子节点，直接删除；
  • 有右子树，使用后继节点（中序遍历的后一个节点）替代，然后在右子树中删除该后继节点；
  • 没有右子树，但有左子树，使用前驱节点（中序遍历的前一个节点）替代，然后在左子树中删除该前驱节点；

  1. insertIntoBST 还是二叉搜索树，找到对应的空节点，将其链接到父节点即可。

  2. isValidBST 因为所有的左右子树都要满足二叉搜索树，所以需要加个上下限，防止如下情况出现：

    5
 \
 6
/ \
3  7

    if (root->val <= min || root->val >= max) {
  return false;
}

  3. nextGreaterElement 这题需要使用哈希表和堆栈，用 c 语言写不方便，故用 c++ 。但是核心都是一样的，

    for (int i = 0; i < nums2Size; i++) {
  while (!Empty(s) && Top(s) < nums2[i]) { // 栈非空，同时栈顶元素要大于当前需要比较的元素
    Pop(s);
  }
  tmp[i] = Empty(s) ? -1 : Top(s); // 后面的元素中有比该元素大的
  Push(s, nums2[i]);
}

  4. maxSlidingWindow 这题用了一个单调队列，这个队列中的元素是单调递增（递减）的。对于给定的数组，将每个元素入队，因为队列是单调的，所以如果队尾的元素小于将要入队的元素，那么将队列中的元素删除，

    for (int i = 0; i < k; i++) {
  while (head < tail && nums[i] > nums[q[tail - 1]]) {
    tail--;
  }
  q[tail++] = i;
}

    同时需要注意的是队列保存的是该元素的索引。窗口每向后移动一次，将新加的元素入队，如果该元素最大，那么队列前面保存的元素自然就被删除了，如果不够大，该元素入队之后也到不了队列头部。这样入队之后，因为队列的头部始终是这个窗口的最大值，那么直接保存队列头部元素即可。如果该头部已经不在该窗口范围，需要更新队列头部。

    while (q[head] <= i - k) {
  head++;
}

    直接用双端队列，更好用。

  5. mergeTwoLists 定义一个 next 指向两个链表中值较小的那个，然后将较小的那个链表表头指向下一个元素，再重复进行下一个比较。

  6. mergeKLists 思路很简单，就是不断的两两合并，利用上一题的代码，大部分时间用在调整指针上。开始只是给每个 ListNode 赋值了，但是没有将节点链接起来，所以在 mergeTwoLists 中访问 list2->next 总是报空指针异常。需要注意阿。

  7. designTwitter 这题超时了，没有通过。先记录一下思路。首先是几个关键的数据结构：

      struct Tweet {
    int tweetId;
    int time;
    struct Tweet *next;
  };

  struct User {
    int userId;
    int followed[501];
    int follows_nums;
    struct Tweet *head;
  };

  typedef struct {
    struct Tweet *tweet;
    struct User *user[501];
    int timestamp;
  } Twitter;

    每个 User 都有自己的 Tweet 和 follow 列表，当需要输出自己和 follow 的前 10 条 tweet 时，将需要计算的几个 tweet 列表集中到 struct Tweet **res; 中，然后用上一题的 mergeKLists 来将所有的列表按照时间顺序排列，输出前 10 个。

  8. reverseBetween 这题思路不难，主要是实现需要想清楚，之后遇到链表的题目要画图帮助理解。记录 left 的前一个节点和 right 的后一个节点，用于之后的链接。记录 reverse list 的头尾节点，用于链接。

  9. permute 这题使用回溯法，这幅图清晰的解释了什么是回溯法。 即选择路径，遍历该路径下所有的节点，当达到结束条件后返回，恢复路径，进行回溯。

  10. permuteUnique 套用上一题的代码，只是需要去除重复的元素，

      if (i != first && isRepeat(nums, first, i)) {
    continue;
  }

  bool isRepeat(vector<int> nums, int start, int end) {
    for (int i = start; i < end; i++) {
      if (nums[i] == nums[end]) {
        return true;
      }
    }

    return false;
  }

  11. solveNQueens 还是用上一题的框架，但是将 isRepeat 换成 isConflict，如果没有冲突则将该位设为 Q，遍历完后再恢复。

    for (int col = 0; col < n; col++) {
  // check conflict if row[nrow][col] = Q
  if (!isConflict(row, nrow, col, n)) {
    continue;
  }
  // if don't have conflict
  row[nrow][col] = 'Q';
  backtrace(board, row, nrow + 1, n);
  // this column has tried, recover to '.'
  row[nrow][col] = '.';
}

  12. totalNQueens 和上题一样。

  13. getPermutation 过于困难，暂时搁置。重新尝试后算法是正确的，但是超时了。这题和上一题的不同之处在与需要按顺序排列所有情况，那么就需要在交换元素之后按照元素的大小重新排列顺序，之后再恢复。

    for (int i = first; i < len; i++) {
  swap(nums[i], nums[first]);
  tmp = i;
  while (tmp > first + 1) {
    swap(nums[tmp], nums[tmp - 1]);
    tmp--;
  }
  backtrace(res, nums, first + 1, len);
  tmp = first + 1;
  while (tmp < i) {
    swap(nums[tmp], nums[tmp + 1]);
    tmp++;
  }
  swap(nums[i], nums[first]);
}

    例如在序列 12345 中，如果交换2 5，数组变成 15342，这时如果进行回溯顺序就不对，因此将其调整为 15234。

  14. nextPermutation 这题思路是这样的，找到第一个升序的 a[i - 1] 和 a[i]，因为都是降序没有下一个更大的序列，然后再从后往前遍历，找到尽可能小的比 a[i - 1] 大的 a[j]，交换 a[i - 1], a[j]，将 a[i - 1] 后面的数按升序重排。因为 a[i ~ n] 为降序，所以直接用 reverse 交换顺序即可。

  15. subsets 这题还是使用回溯法，但是遍历方法有所不同。首先是结束条件，子集需要将所有的路径添加进去，而排列只要 n = nums.size() 时才添加。然后是回溯状态的变化，

    backtrace(trace, nums, i + 1);

  16. subsetsWithDup 这题和上一题基本一样，但是由于有重复元素，需要跳过，

    if (!(i > 0 && nums[i] == nums[i - 1] && i > n)) {
   trace.push_back(nums[i]);
} else {
  continue;
}

    需要判断 i > n 是为了避免如下情况：

              O
   1/    2|   2\(1)
   O      O    O
 2/ \2   2|(2)
 O  O     O
2|
 O

    情况（2）的 22 这个子集是符合要求的，但是如果按照 nums[i] == nums[i - 1] 条件会将其排除，也就是说只有两个元素在同一层级上相等才需要去除，如情况（1）就是两个 2 在同一层次。

  17. combine 这题比较简单，还是用回溯的框架，然后结束的条件是

    if ((int)trace.size() == k) {
  res.push_back(trace);
  return;
}

  18. search

    复习一下二分查找。

  19. searchRange 用二分查找，比较简单。

  20. hasCycle 用双指针法。

  21. detectCycle 这里可以通过数学方法证明这个情况：当发现 one 与 two 相遇时，再额外使用一个指针 p。起始，它指向链表头部；随后，它和 one 每次向后移动一个位置。最终，它们会在入环点相遇。

  22. twoSum 开始想用回溯法，因为就是求两个数的和，跟 [combine](53. combine) 一样。但是会超时。还是需要使用双指针法，只要数组有序，就应该想到双指针技巧。

  23. threeSum

    唉，我想到的回溯法其实是暴力排序，

      void backtrace(vector<int> nums, vector<int> tmp, int first, int len) {
    if ((int)tmp.size() == 3) {
      if (tmp[0] + tmp[1] + tmp[2] == 0) {
        res.push_back(tmp);
      }
      return;
    }

    for (int i = first; i < len; i++) {
      tmp.push_back(nums[i]);
      backtrace(nums, tmp, i + 1, len);
      tmp.pop_back();
    }
  }

    其实可以用简单的双指针，

      vector<vector<int>> threeSum(vector<int> &nums) {
    vector<vector<int>> res;
    int n = (int)nums.size();
    if (n < 3)
      return res;
    sort(nums.begin(), nums.end()); // 先排序，方便之后跳过重复的元素
    for (int i = 0; i < n; i++) {
      if (nums[i] > 0) // 如果 nums[i] > 0, nums[left] + nums[right] + nums[i] 肯定大于 0
        return res;
      if (i > 0 && nums[i] == nums[i - 1]) { // 跳过重复的元素
        continue;
      }

      int left = i + 1, right = n - 1; // left, right 在 nums[i, n - 1] 中遍历
      while (left < right) {
        int sum = nums[left] + nums[right] + nums[i];
        if (sum > 0) {
          right--;
        } else if (sum < 0) {
          left++;
        } else {
          res.push_back({nums[left], nums[right], nums[i]});
          while (right > left && nums[right] == nums[right - 1]) // 去除重复的元素
            right--;
          while (right > left && nums[left] == nums[left + 1])
            left++;
          left++;
          right--;
        }
      }
    }
    return res;
  }

  24. fourSum

    好吧，没什么技术含量，就是硬算，用双指针比 O(n^4) 好一点，就是细节很难调。

  25. findDuplicate 这题确实想不到，在数组中使用双指针。因为有两个重复的数，那么有一个元素一定有两个入口，和判断链表是否有环一样的。找到有两个入口的点后再用链表中找环入口的方法即可找到对应的元素。

  26. minWindow 这题使用滑动窗口法，该方法可以分为如下几步： （1）在数组中维持 left, right 指针，将 s[left, right] 称为一个 window， （2）先不断增大 right 指针，直到 window 中的字符串符合条件，记录下 window 的长度， （3）停止增加 right 指针，转而不断增加 left 指针，直到 window 中的字符串不再符合条件， （4）重复（2）（3）部，直到 s 的末尾。 而这里有一个问题就是如何判断 window 中的字符串是否满足条件，这里使用了 unordered_map 当作计数器，unordered_map 会记录每个字符出现的次数，如果该字符在 need 中存在，那么这个字符就需要加入 has，如果 (int)has[tmp] == (int)need[tmp] 就说明这个字符已经匹配好了，将计数器加 1。如果所有的字符都匹配好了，那么 left 开始增加，直到 (int)has[tmp] < (int)need[tmp]说明 window 中的字符串已经不能匹配 need，进行下一次循环。

  27. lengthOfLongestSubstring 还是用滑动窗口，和上题类似，维护 left, right 指针，检查 s[right] 在 window 中是否存在，如果存在则将 has[s[left]] 置为 0，将 left 加 1 ，直到 window 中没有该字符，再将该字符加入 window，right 指针加 1。

  28. findAnagrams 还是使用滑动窗口，注意判断 window 中的字符串是否满足的条件是 match == (int)need.size()

  29. checkInclusion 和上一题一样，只是修改一下返回值。

  30. longestSubarray

    这题开始的做法是使用滑动窗口，但是要不断寻找窗口内的最大最小值，最后一个测试案例会超时，所以使用双端队列维护最大最小值，

        deque<int> maxq, minq;
    int res = 0;
    int n = (int)nums.size();
    int left = 0, right = 0;
    int tmp;
    while (right < n) {
      tmp = nums[right];
      while (!maxq.empty() && maxq.back() < tmp) {
        maxq.pop_back(); // 确定到目前为止的最大值
      }
      while (!minq.empty() && minq.back() > tmp) {
        minq.pop_back(); // 确定到目前位值的最小值
      }

      maxq.push_back(tmp);
      minq.push_back(tmp);

      while (!maxq.empty() && !minq.empty() &&
             maxq.front() - minq.front() > limit) {
        if (maxq.front() == nums[left]) {
          maxq.pop_front(); // nums[left] 就是最大值，所以要出栈
        }
        if (minq.front() == nums[left]) {
          minq.pop_front(); // nums[left] 就是最小值，所以要出栈
        }
        left++;
      }
      res = max(res, right - left + 1);
      right++;
    }
    return res;

    本来想用 queue<int> 的，但是不能从后端出栈，所以出错了。

  31. floodFill 这题需要遍历二维矩阵，使用多叉树的遍历，

    DFS(image, row + 1, col, origincolor, newColor);
DFS(image, row, col + 1, origincolor, newColor);
DFS(image, row - 1, col, origincolor, newColor);
DFS(image, row, col - 1, origincolor, newColor);

    同时考虑返回条件，即该元素的颜色和 origincolor 不一样，或者超出数组范围。

    同时为了在遍历邻居是不会重复遍历原来的节点，需要暂时将原来的节点的值设为非法值，

    image[row][col] = -1; // [row, col] should not be check from it's neighbors

  32. islandPerimeter 这题使用和上一题一样的模板，但是需要找到一块陆地作为搜索起点，同时需要避免重复遍历，将遍历过的元素置为 2。

  33. maxAreaOfIsland 还是一样的，不过这里是计算符合条件的元素个数，所以返回值需要修改一下，

    return 1 + DFS(grid, row + 1, col) + DFS(grid, row, col + 1) +
         DFS(grid, row - 1, col) + DFS(grid, row, col - 1);

  34. numIslands 同上。

    这里可以不用像上面那样，因为 grid[i][j] == '1' 说明这肯定是一块陆地，直接 num++ 就行。

  35. solve 任何边界上的 'O' 都不会被填充为 'X'，所以我们可以遍历所有在边界上的 'O'，将其转换为 ‘2’，然后使用 FloodFill 算法，遍历四周的元素，将所有不符合条件的元素替换成‘2’，这样所有与边界 ‘0’ 相连的节点都会被转化为 ‘2’，而不相连的则还是 ‘O‘，然后遍历整个矩阵，将所有 ‘O’ 转换为 'X'，将 ‘2’ 转换为 ‘O’。

  36. equationsPossible 这题很抽象，不太懂。首先使用的是 UnionFind 算法，这个算法需要实现 3 个 API，

    • union：将两个节点所在的树连接，这需要用到 find，即找到该节点的父节点，将一颗树的父节点指向另一棵树即可。这样连接的话如果节点 p 和 q 连通的话，它们一定拥有相同的根节点；
    • find：找到该节点的父节点。这里还顺带做了压缩操作，对这个操作还不懂，不用这个优化也行。
    • connected：两个节点所在的树是否是连接的。而将 UnionFind 算法应用到这题是这样的： 首先将所有等式两端的值代表的节点通过 union 建立连接，然后遍历所有不等式，如果不等式两端的值已经连接了，那么该等式组就不成立。

  37. validateBinaryTreeNodes

    还是使用 UnionFind 算法，其判断是否成环的方式是在连通前检查两个节点是否是连接的，如果是，那么就会成环，

            if (uf->connected(i, leftChild[i])) {
          return false;
        }
        uf->_union(i, leftChild[i]);

    然后还要检查所有节点的入度，正常情况下只有一个根节点（入度为 0），然后剩余的节点入度都为 1，

        int root = -1;
    for (int i = 0; i < n; i++) {
      if (degree[i] == 0) {
        if (root != -1) {
          return false; // only one root
        }
        root = i;
      } else if (degree[i] != 1) {
        return false; // no node has more than one indegree
      }
    }

    if (root == -1) {
      return false;
    }

  38. pancakeSort 烧饼排序，找到前 n 个烧饼中最大的那个，将其反转到第一个，然后整个反转，那么最大的那个就到了位置 n，完成了一个烧饼的排序，然后递归的排序 n - 1 个烧饼即可。

  39. shuffle 洗牌算法，核心思想就是产生 n! 种可能。

      for (int i = 0; i < size; i++) {
    r = rand() % (size - i) + i;
    swap(num[i], num[r]);
  }

    然后 c++ 写法要注意类的初始化，

      this->size = (int)nums.size();
  this->num = nums;
  this->tmp.resize(size); // this is important
  for (int i = 0; i < size; i++) {
    this->tmp[i] = nums[i];
  }

  40. hammingWeight 这题是位操作的题，记录几个有趣的位操作：

    • 利用或操作 | 和空格将英文字符转换为小写

      ('a' | ' ') = 'a'
('A' | ' ') = 'a'

    • 利用与操作 & 和下划线将英文字符转换为大写

      ('b' & '_') = 'B'
('B' & '_') = 'B'

    • 利用异或操作 ^ 和空格进行英文字符大小写互换

      ('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'

    • 不用临时变量交换两个数

      int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;

    • 消除数字 n 的二进制表示中的最后一个 1

      n &= (n - 1);

  41. reverseBits 同样是位操作，比较简单，将 n 的二进制最后一位左移 31 - tmp 位即可。但是要多做几道，增加熟练度。

  42. isPowerOfTwo 某个数是 2 的幂说明该数的二进制表示中只有一个 1 。

  43. isPowerOfThree 这种题目不用位操作也行，不过效率更低一点。

  44. isPowerOfFour

    简单。

  45. missingNumber

    好吧，用异或更简单。

  46. multiply 这题可以用作大数乘法，即按照手算的方式做乘法。这里有一点需要特别注意，num1[i] * num2[j] 相乘结果是在 res[i + j] 和 res[i + j + 1] 中，然后需要加上上一次的结果，再将个位和十位分别存放在 res[i + j] 和 res[i + j + 1]。

    for (int i = size1 - 1; i >= 0; i--) {
    for (int j = size2 - 1; j >= 0; j--) {
      mul = (num1[i] - '0') * (num2[j] - '0');
      p1 = i + j;
      p2 = i + j + 1;
      sum = mul + tmp[p2];
      tmp[p1] += sum / 10;
      tmp[p2] = sum % 10;
    }
}

  47. addTwoNumbers 思路比较简单，就是正常的加法，然后进位就行，但是要处理最高位不能为 0 的情况，需要加一个判定条件：

    if (next1 != NULL || next2 != NULL || sum / 10 != 0) {
   ListNode *tmp = new ListNode;
   p->next = tmp;
   p = tmp;
   p->val = sum / 10;
}

    还需要处理的一个情况就是 l1 和 l2 长度可能不相等，所以也要加个防溢出的操作，

      if (pl1 != NULL) {
    pl1 = pl1->next;
  }
  if (pl2 != NULL) {
    pl2 = pl2->next;
  }

  48. merge 这题解法不难，但是细节调整花了很久。首先需要将数组按照首区间左端点从小到大排列，那么二维数组第一个区间的左端点就是整个区间最小的点。然后遍历后面的区间，如果左端点小于该区间的右端点，那么说明这两个区间相互重叠，将目前的右端点调整为两个区间的最大值，继续遍历。

    for (int i = 0; i < (int)intervals.size();) {
    max = intervals[i][1];
    int j = i + 1;
    while (j < (int)intervals.size() && intervals[j][0] <= max) {
      max = max > intervals[j][1] ? max : intervals[j][1];
      j++;
    }
    res.push_back({intervals[i][0], max});
    i = j;
}

  49. insert 这题和上一题一样，只是将新的区间加进去即可。

  50. findPoisonedDuration 还是利用上一题的思路，根据开始值和时间间隔构建出区间，然后进行合并，计算合并后的长度即可。

  51. intervalIntersection 思路类似，将两个 list 合成一个，然后计算重叠区域，只不过这次需要记录的是 list[j][0] 和 list[j][1] < max ? list[j][1] : max。

  52. removeCoveredIntervals

    和上面一样的思路，计算多少个重复的区间即可。

  53. subarraySum 这题需要用到前缀和，即保存 nums[0 ~ i) 的和 sum[i] ，然后 nums[i ~ j] 的和就等于 sum[j + 1] - sum[i] 。但这题还需要在前缀和的基础上优化计算任意一个子串是否满足和为 k 即计算 sum[j + 1] - sum[i] == k 是否成立，我们可以将这个式子转化为 sum[i] == sum[j + 1] - k 是否成立，那么我们需要计算在前面已经计算的子串中是否有满足条件的，如果有，那么直接加上该前缀和出现的次数即可。

  54. checkSubarraySum 这题和上一题有点不同，需要满足子数组元素总和为 k 的倍数，如果还是像上题那样将所有的前缀和保存下来，那么只能一个个遍看是否满足。这里有一个性质，当 sum[j] - sum[i] == nk 时，sum[j] 和 sum[i] 除以 k 的余数相等。所以存储余数和产生该余数的位置，然后就和上一题一样了。同时由于还需要满足子数组大小至少为 2 ，所以除非 map 中不存在该余数，否则不要更新 map，不然会导致 5 0 0 0 0 判断错误的情况，因为余数一直为 2，每次都更新就不能满足子数组大小至少为 2。这里还需要注意 unordered_map 的使用方法，像数组一样使用就行。

  55. maxEnvelopes 有趣，官方答案超时。这题和 LengthOfLIS 一样，时间复杂度同样是 n^2。同样是用 dp[i] 记录到 i 为止的最多信封数量。

  56. minEatingSpeed 这题居然使用二分法做，好吧，我没有想到。left = 1, right = max。

  57. shipWithinDays 和上一题一样，修改一下 left、right 和 isMatch 即可。从这两题可以看出来，只要是需要暴力遍历连续整数的题目都可以使用二分法。

  58. reverseKGroup 这题关键点有两个，一是怎样反转 l[a, b) 之间的节点，这里用 reverse 函数来做，

      ListNode *reverse(ListNode *a, ListNode *b) {
    ListNode *pre, *cur, *next;
    cur = a;
    pre = NULL;
    while (cur != b) {
      next = cur->next;
      cur->next = pre;
      pre = cur;
      cur = next;
    }

    return pre;
  }

    反转方法结合这张图更好记。另一个是如何递归反转，这个思想不难，就是反转第 k 个节点之后的节点。但是要理清楚反转后的节点是如何链接起来的。

  59. swapPairs 这题和上题一样，都是反转链表。

  60. canWinNim 额，解法很简单，谁在取石头的时候石头数是 4 的倍数就输了。

  61. bulbSwitch 只有被按下奇数次的灯泡最后才是亮着的，所以只有因子个数为奇数的灯泡序号才会亮，只有平方数的因子数为奇数（比如 6 = 1 * 6, 2 * 3，它们的因子总是成对出现的，而 4=1 * 4, 2 * 2，只有平方数的平方根因子会只出现 1 次），所以最终答案等于 n 以内（包括 n 和 1）的平方数数量，只要计算 sqrt(n)即可。

  62. isSubsequence

  63. isPalindrome 关于单链表的实用技巧： （1）通过「双指针技巧」中的快慢指针来找到链表的中点：

    ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
  slow = slow.next; // middle node
  fast = fast.next.next;
}
if(fast != NULL){
  slow = slow.next; // lenght of link is odd
}

    这题使用快慢指针找到中间节点后将后半部分反转，再比较即可。

  64. isValid 使用 stack 即可，是匹配的就 pop，不是的就 push，最后看 stack 是否为空。

  65. generateParenthesis 这题使用之前学过的回溯法加上上一题的 isValid。回溯法能够生成所有可能的情况，再用 isValid 一一判断。

  66. minAddToMakeValid

    同样可以利用上面的方法，最后返回栈的大小即可。

  67. minInsertions

    这题做法和前面的不一样。遍历字符串，通过一个 need 变量记录对右括号的需求数，根据 need 的变化来判断是否需要插入。当 need == -1 时，意味着我们遇到一个多余的右括号，显然需要插入一个左括号。另外，当遇到左括号时，若对右括号的需求量为奇数，需要插入 1 个右括号，因为一个左括号需要两个右括号嘛，右括号的需求必须是偶数。

    我们调试一下 )))())( 这个案例就清楚了。

  68. letterCombinations

    回溯法，比较简单。

  69. removeDuplicates 简单。

    用双指针更简单。

  70. removeDuplicates_ii 和上一题一样，只是改成了每个元素最多出现两次。

  71. countPrimes 这题用 tmp = sqrt(n) 解还是超时，学会了一种新的方法，排除法。从 2 开始，如果 i 是前面的数的倍数，那么 i 肯定不是素数。从 2 遍历到 sqrt(n)，将所有的非素数排除，再计算即可。

  72. numSquares

    这也能用动态规划是我没想到的，

    动态转移方程：dp[i] = 1 + min(dp[i - j * j]) (1 < j < sqrt(i))

    dp[i] 表示最少需要多少个数的平方来表示整数 i。

    这些数必然落在区间 [1, sqrt(n)]。我们可以枚举这些数，假设当前枚举到 j，那么我们还需要取若干数的平方，构成 i - j^2。

    dp base：dp[0]= 0

  73. isUgly 这题要读懂题目，是只包含质因数 2, 3, 5 的整数。

  74. nthUglyNumber 不能直接用上一题的方法，时间复杂度太高，这里使用动态规划法。第 i 个 uglynumber 等于 min(2 * dp[p2], 3 * dp[3], 5 * dp[5]) ，然后不断调整指针即可。这里有一点需要注意，当 2 * dp[p2] == 3 * dp[p3] 时，p2 和 p3 都需要调整，如果只调整了一个指针，那么下一次计算最小值还是 2 * dp[p2] 或 3 * dp[p3]。

  75. nthSuperUglyNumber 这题只是上一题的变形，将几个质因子换成一组质因子即可。不过如果没有上一题直接写这题肯定写不出来。

  76. maxArea

    想出来了是用双指针法，但是维护指针的方法错了，应该移动值较小的那个指针。

  77. trap

    还是使用双指针法，不过更难想到。首先明确一个事情，还是要移动值较小的那个指针，第 i 个柱子能够接的水量等于 leftmax - height[left] 或 rightmax - height[right]，其他的也没啥高深的知识，能想到就做的出来。

  78. productExceptSelf

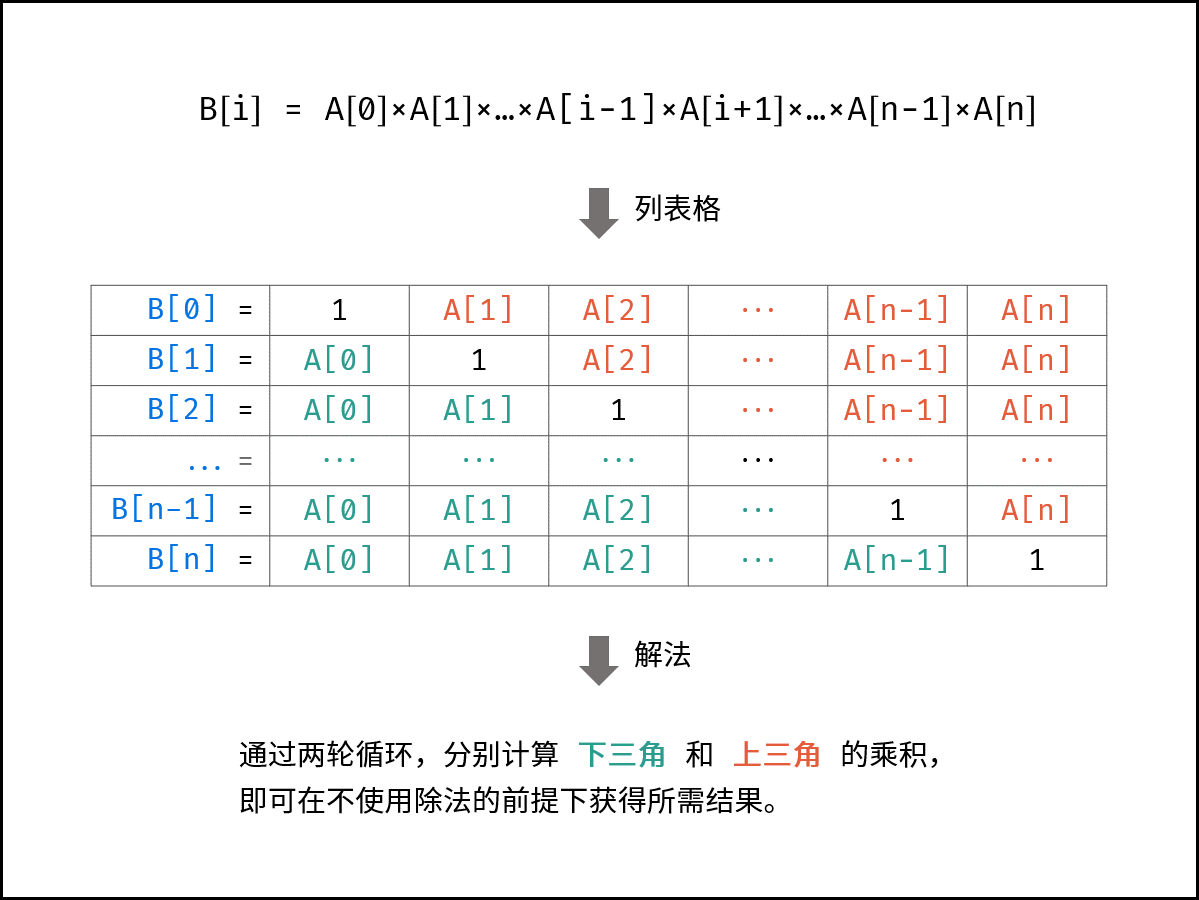
    这题解法很巧妙，维持两个数组，left[i] 和 right[i] 分别表示第 i 个数左边数的乘积和右边数的乘积，最后的结果就是 left[i] * right[i]。

    for (int i = 1, j = size - 2; i < size && j >= 0; i++, j--) {
  left[i] = left[i - 1] * nums[i - 1];
  right[j] = right[j + 1] * nums[j + 1];
}

  79. linkRandom

    就是正常的用 rand() 求随机数。

  80. randomIndex

    原来随机数也有技巧：当遇到第 i 个元素时，应该有 1/i 的概率选择该元素，1 - 1/i 的概率保持原有的选择。

  81. randomPickWithBlacklist

    这题很巧妙，如果遍历 [0 ~ n -1] 会超时，所以把所有小于 this->size = n - (int)blacklist.size(); 且在黑名单中的数一一映射到大于等于 this->size = n - (int)blacklist.size(); 且出现在白名单中的数。这样一来，如果随机生成的整数出现在黑名单中，我们就返回它唯一对应的那个出现在白名单中的数即可。

  82. findDisappearedNumbers

    一般的思路是设置一个 hash 表，记录所有出现过的元素，但这样空间复杂度是 O(n)。这里将索引为 nums[i] - 1 的元素加 n，如果某个值没有出现，那么以该值作为索引的元素值就会小于等于 n，这样就能在原地找出没有出现的元素。

  83. findDuplicates

    和上一题类似，只需要将判断条件改成 nums[(nums[i] - 1) % n] > 2 * n。

  84. findErrorNums

    同样的思路，最重要的还是如果某个数字重复出现，那么以它为索引的元素在加上 n 之后必定大于 2n，而如果某个数没有出现，那么以它为索引的元素在遍历结束后必定小于 n。

  85. pickIndex

    这题思路很简单，计算前缀和 pre[i] 和所有权重的和 sum ，产生一个在 [1 ~ sum] 的随机数，这个随机数落在哪个前缀和内结果就是这个数。当然这个确定的过程可以用二分法做。

  86. minDepth

    基本的层序遍历（BFS）。这里是求最小深度，那么就每次遍历完所有的队列节点再进入下一层，如果遇到叶子节点就返回。要求最大深度的话那就就要队列为空时，即所有的节点都遍历完了再返回。

  87. maxDepth

    上题已经分析了。

  88. levelOrder

    同样的层序遍历，按层加入 vector 即可。

  89. isBalanced

    递归的判断子树是否平衡。如果左右子树的高度差大于 1，那么返回 -1，如果左右子树不平衡，那么该子树也不平衡，返回 -1，否则返回在左右子树的高度上加 1 再返回。

  90. maxDepthOfNTree

    还是层序遍历，只是修改一下加入队列的方式即可。

  91. levelOrderBottom

    在层序遍历的基础上修改一下入队顺序即可。

    res.insert(res.begin(), tmp);

  92. averageOfLevels

    还是层序遍历。

  93. preorderOfNTree

    正常的前序遍历，调整一下递归方法即可。

  94. zigzagLevelOrder

    在层序遍历的时候计算层数，根据层数确定入队的顺序。

  95. diameterOfBinaryTree

    二叉树递归的返回值应该是要求什么返回什么，比如这题要求的是树的最大高度，所以返回最大高度，

    return max(leftheight, rightheight) + 1;

    而求长度最大值则是在递归的过程中不断用子树的长度和当前最大长度比较，确定最大值。

  96. invertTree

    相当于后序遍历的变形。

  97. flatten

    在前序遍历的时候如果将右子树不为空，那么将右子树入栈，然后将左子树调整到右子树的位置，将左子树指针设为空指针。然后递归的遍历右子树（原左子树），如果右子树为空（所有的左子树都遍历完了），那么递归的遍历所有入栈的原来的右子树。

  98. connect

    同样是层序遍历，将节点的 next 指针指向栈顶元素即可。

  99. connect_ii

    额，和上一题一模一样，相当划水。

  100. rightSideView

    继续划水，层序遍历。

  101. constructMaximumBinaryTree

    按照题目意思写， （1）创建一个根节点，其值为 nums 中的最大值。 （2）递归地在最大值 左边 的 子数组前缀上 构建左子树。 （3）递归地在最大值 右边 的 子数组后缀上 构建右子树。 这里要注意如果最大的元素就是在最左边或最右边，那么就不要构建左/右子树。

  102. buildTree_ii

    关键点就是后序遍历的最后一个元素是根节点，根据这个根节点在中序遍历中找到左右子树，然后递归的构建即可。这里要注意左右子树的索引。

  103. serializeDeserialize

    开始想用求出该二叉树的中序和后序遍历的结果存储在同一个字符串作为序列化结果，然后用根据中序和后续遍历求二叉树的方法来进行反序列化，但是无法解决有节点元素相同的情况。其实解法很简单，序列化就是前序遍历，将空指针用 # 代替，反序列化也是前序遍历，遇到 # 返回空指针。然后为了应对负数的情况，将每个节点的值转化成 string 类型后用 , 隔开。

  104. findDuplicateSubtrees

    学到了，通过前序遍历序列化二叉树时，如果不用全局 str 变量，而是每个子树创建一个 str，那么就可以记录每个子树的前序序列化。这时再使用 map，就可以找到重复的子树。

  105. kthSmallest

    二叉搜索树的中序遍历就是所有元素从大到小排列的。

  106. convertBST

    受到 127 题启发，先中序遍历将所有节点的值按顺序输出，然后从后遍历，计算大于等于原节点的值之和。之后再中序遍历一次，将新值写回即可。

  107. searchBST

    简单的二叉树搜索。

  108. numTrees

    这题需要数学分析一下，题目要求计算长度为 n 的序列能够构成不同二叉搜索树的个数， 我们定义两个函数： （1）G(n): 长度为 n 的序列能够构成不同的二叉搜索树的个数。 （2）F(n, i): 以 i 为根节点，长度为 n 的序列能够构成不同的二叉搜索树的个数。 那么 G(n) = sum(F(n, i))(1 <= i <= n) F(n, i) = G(i - 1) * G(n - i) 所以 G(n) = sum(G(i - 1) * G(n - i))(1 <= i <= n)

    不过这样做很难想到，下面使用另外一种方法，

    假设给算法输入 n = 5，也就是说用 {1,2,3,4,5} 这些数字去构造 BST。如果固定 3 作为根节点，左子树节点就是 {1,2} 的组合，右子树就是 {4,5} 的组合，那么 {1,2} 和 {4,5} 的组合有多少种呢？只要合理定义递归函数，这些可以交给递归函数去做。

    另外，这题存在重叠子问题，可以通过备忘录的方式消除冗余计算。

  109. generateTrees

    和上一题类似，不过我还是不能独立做出来。这里分解成的子问题是生成左右子树的序列。

    	for (int i = left; i <= right; i++) {
      vector<TreeNode *> lchild = generate(left, i - 1);
      vector<TreeNode *> rchild = generate(i + 1, right);

      for (auto l : lchild) {
        for (auto r : rchild) {
          TreeNode *root = new TreeNode(i, l, r);
          res.push_back(root);
        }
      }
    }

    不得不说，这种分解思想是有效的，还需要多加练习。

  110. findTarget

    这题比较简单，用 unordered_map 即可。

  111. maxSumBST(not pass)

    我觉得这道题的关键是判断每棵树是否是二叉搜索树，如果是的话就将这棵树加入到队列中，然后再从对立的所有二叉搜索树中找到最大的那颗，但是我不会。

  112. minDiffInBST

    这题的解法就是上面重要思想的体现。

      void inorder(TreeNode *root) {
    if (!root) {
      return;
    }

    inorder(root->left);
    if (pre) {
      res = min(res, root->val - pre->val);
    }
    pre = root;
    inorder(root->right);
  }

    中序遍历，那么在中间操作的就是父节点，pre 一定是左子树节点或父节点，递归会对所有的节点做同样的操作。

  113. lowestCommonAncestor

    首先找到所有节点的父节点，记录在一个 map 中，

    void getFather(TreeNode *root) {
  if (root->left != NULL) {
    father[root->left->val] = root;
    getFather(root->left);
  }
  if (root->right != NULL) {
    father[root->right->val] = root;
    getFather(root->right);
  }
}

    然后根据父节点的记录遍历 q 的所有父节点，将遍历过的节点也记录下来，之后再遍历 p 所有的父节点，在遍历过程中，如果该节点已经被遍历过了，那么该节点就是 LCA。

  114. countNodes

    层序遍历一下计数即可。

  115. allPathsSourceTarget

    这题使用回溯法(DFS)遍历所有的路径，从第一个节点开始，遍历每个节点相连的节点，如果该节点是末端节点，那么这条路径就是一个符合条件的路径。

  116. canFinish

    开始想的是建立一个哈希表，记录哪些节点已经完成了，如果某个节点所有的需求都已经完成了，那么这个节点也可以完成。之后遍历哈希表，如果有节点没有完成，那么返回 false。这是其实是求是否存在一个拓扑排序，可以采用 dfs 来求。我们将每个节点的状态分为三种： （1）未搜索：还没有搜索到这个节点； （2）搜索中：已经搜索过这个节点，但还没有回溯到该节点，其还有相邻的节点没有入栈； （3）已完成：已经搜索并完成该节点，可以入栈。

    那么使用这三种状态，我们可以设计出求拓扑排序的算法，首先建立每个节点的出度，

    for (int i = 0; i < (int)prerequisites.size(); i++) {
  edges[prerequisites[i][1]].push_back(prerequisites[i][0]);
}

    遍历该节点的相邻节点即遍历所有的出度。然后遍历每个节点，如果该节点的状态是“未搜索”的话，

    for (int i = 0; i < numCourses && valid; ++i) {
  if (!visited[i]) {
    dfs(i);
  }
}

    搜索该节点的所有相邻节点，如果该相邻节点的状态是未搜索，那么对其进行 dfs 递归，如果该节点的状态是“搜索中”，那么不存在拓扑排序，返回 false，在所有的相邻节点遍历完后，该节点的状态变为“已完成”。

    拓扑排序：对一个有向无环图 （Directed Acyclic Graph 简称 DAG）G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边 <u,v>∈E(G)，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序（Topological Order）的序列，简称拓扑序列。

    当然，如果是要构建一个拓扑排序，需要用到 BFS，不断找到入度为 0 的节点，然后入栈。

  117. findOrder

    和上题一样的拓扑排序，只需要额外创建一个数组，用于保存序列，当该节点的状态为“已完成”时就可以将其加入到路径中。

  118. findMinHeightTrees

    暴力 BFS，超时。

  119. isBipartite

    这里使用染色法，算法流程如下： （1）选定任意节点将其染成红色，遍历与该节点相邻的节点；

      color[0] = 1;
  for (int i = 0; i < n && flag; i++) {
    dfs(i, 1, graph);
  }

    （2）如果该节点是红色，且相邻节点也被染色了，但是颜色和该节点相同，那么返回 false，如果相邻节点没有被染色那么将相邻节点染成黄色；如果该节点是黄色，操作类似；

      if (color[n] == 1) {
    if (color[graph[n][i]] != 0) {
      if (color[graph[n][i]] == color[n]) {
        flag = false;
        return;
      }
      continue; // 该节点已经被染色了，不用遍历
    } else {
      color[graph[n][i]] = 2;
    }
  } else if (color[n] == 2) {
    if (color[graph[n][i]] != 0) {
      if (color[graph[n][i]] == color[n]) {
        flag = false;
        return;
      }
      continue;
    } else {
      color[graph[n][i]] = 1;
    }
  }

    （3）如果该节点没有被染色，那么将其染成与父节点不同的颜色。

      if (color[n] == 0) {
    if (n_color == 1) {
      color[n] = 2;
    } else {
      color[n] = 1;
    }
  }

    dfs(n, n_color, graph) 中的 n_color 就表示父节点的颜色。

    细节是魔鬼。

  120. possibleBipartition

    和上一题一样使用染色法，但是需要根据 dislikes 建立无向图。

      for (int i = 0; i < size; i++) {
    // both directions should build connect
    graph[dislikes[i][0]].push_back(dislikes[i][1]);
    graph[dislikes[i][1]].push_back(dislikes[i][0]);
  }

  121. minCostConnectPoints

    这题使用 Kruskal 算法，算法的思路很简单，将所有的边按照长度排序，然后遍历所有的边。如果加入这条边能够连通两个连通子图，那么这条边就是最短路径中的一条边，直到所有的节点都加入最短路径中，结束遍历。这里判断某条边能够连通两个连通子图使用的是 UnionFind 算法。

    用 priority_queue 小顶堆保存边更高效。

  122. networkDelayTime

    dijkstra 算法，以前觉得这算法挺复杂的，现在写一遍也没有那么难啊，就是复杂一点的 bfs。首先 dijkstra 算法的大致思路是这样的：

    • 从 start 节点出发，创建一个 disTo 数组，用来记录其他节点到 start 节点的距离，初始时除 start 为 0 其他都为 INT_MAX；
    • 同时为每个节点维护一个入栈结构 vector<int> tmp ，tmp[0] 表示该节点的索引，tmp[1] 表示该节点到 start 节点的距离；
    • 如果遍历到某个节点，该节点 tmp[1] > disTo[] ，那么说明这条路肯定不是最优的，这个节点就直接跳过，不用遍历；
    • 否则遍历该节点所有的邻接节点，更新邻接节点到 start 节点的距离 int nextNodeToStart = graph[curNode][i][1] + disTo[curNode];，如果这条路径距离更近，那么更新 disTo[i]，同时将该节点入栈；

    然后有几点需要注意： （1）需要根据题目条件建立图，一般是使用邻接表表示，需要注意节点的索引是从 0 开始还是从 1 开始；

  123. maxProbability

    和上一题类似，不过这里建立邻接表时要建立双向的，不然会导致有些情况返回 0。还有就是不需要求所有的路径的可能性，只要求 start -> end 的就可以的了，其他的都一样。

      if (curStateId == end) {
    return {1, curStateProbability};
  }

  124. minimumEffortPath

    还是按照上面的模板，这里需要遍历当前节点的 4 个相邻节点（如果 4 个相邻节点都没有越界的话），然后 vector<vector<int>> heightTo(row, vector<int>(col, INT_MAX)); 记录的是当前节点的最大高度差，如果相邻节点与当前节点的高度差大于 heightTo[curNodex][curNodey] 就需要更新，

            int heightBetween =
            abs(heights[nextNodex][nextNodey] - heights[curNodex][curNodey]);
        heightBetween = max(heightBetween, heightTo[curNodex][curNodey]);

  125. findCheapestPrice

    还是 dijkstra 算法，但是加了“最多经过 k 站中转的路线“这一限制，有些案例不能通过，比如这个，

    4
[[0,1,1],[0,2,5],[1,2,1],[2,3,1]]
0
3
1

  126. implementTrie

    Trie，前缀树或字典树，可以理解为多叉树，每个叉即表示字典中的一个元素，然后每个节点包含一个指示该节点是否为字符串结尾的标识符。

    vector<Trie *> children;
bool isEnd;

    由于 word 和 prefix 只由小写字母组成，所以初始化为 26 叉树，即有 26 个子节点。

    Trie() : children(26), isEnd(false) {}

    • 插入操作 在插入字符时，如果当前的树中没有该字符对应的节点，那么创建一个节点，

      if (node->children[word[i]] == NULL) {
  node->children[word[i]] = new Trie();
}

      当处理到最后一个字符时，需要将当前节点标记为字符串的结尾。

    • 查找前缀 从字典树的根节点开始查找，如果某个字符在树中不存在，说明该前缀不存在，返回 NULL；若搜索到了前缀的末尾，说明该前缀存在，若前缀末尾对应的节点 isEnd 为真，说明存在该字符串。

  127. WordDictionary

    可算过了，折腾人。思路还是一样的，但是要考虑 . 的情况。当 ch == '.' 时，需要用 dfs 遍历该节点所有非空的子结点，同时 word 也要调整，去掉第一个字符。同时还需要考虑 word 虽然能够匹配 trie，但是长度比 trie 短的情况，这种算作不匹配。

  128. replaceWords

    还是和上面一样的做法，但是要考虑一种情况：如果继承词有许多可以形成它的词根，则用最短的词根替换它。所以我们在每次插入字符串结束后都要 node->isEnd = true;，之后在查找的时候每查找完一个字符就检查该字符是否是 node->isEnd = true;。

  129. MapSum

    cao，搞了半天，直接暴力法就行。

  130. dailyTemperatures

    求下一个更大的元素，就是用单调栈解。单调栈即从后面开始遍历，不断将小于当前元素的值出栈，从而找到第一个比当前元素大的值，然后将当前元素入栈。这里由于要求第几天会遇到比当前温度高的温度，所以多存储一个天数信息。

  131. nextGreaterElements

    还是用单调栈，但是因为可以循环遍历，所以遍历两次。

  132. numArraySumRange

    简单的前缀和应用。

  133. numMatrix

    和上一题类似，可以理解为多个数组的和。

  134. countRangeSum

    这题用 dp 能够通过部分案例，但是复杂度太高，难的算法先不学了吧通过部分案例应该也能的部分分。

  135. maxSubarraySumCircular

    这题的做法很巧妙，

        for (int i = 1; i < n; i++) {
      sum += nums[i];
      dp = nums[i] + max(dp, 0);
      _max = max(dp, _max);
    }

    要求值最大的子数组，按我的想法是要遍历两次的，找到所有的 sum[i..j]，不过这里 dp = nums[i] + max(dp, 0); 就可以找到最大值，因为如果前一个子数组和是负数，那么就没有必要加上。

  136. shortestSubarray

    和 149. countRangeSum 类似，O(n^2) 的算法会超时。

  137. corpFlightBookings

    这题用到了差分数组。数组 nums=[1,2,2,4] 的差分数组为 cha=[1,1,0,2]，即 cha[j] = nums[j] - nums[j - 1] 而对差分数组求前缀和即可得到原数组。如果我们要将 nums[i ~ j] 加上某个定值，那么需要将 cha[i] 加上该值，将 cha[j + 1] 减去该值。这题就是不断对数组区间求差分数组，一个预定记录就是对区间的操作。

  138. carPooling

    同样是差分数组，但是有些差别。乘客上先下后上，那么在乘客下车的那个站点就需要减去乘客数量，而不是等到下一个站点再减，即我们需要在 nums[i ~ j - 1] 加上某个定值，那么需要将 cha[i] 加上该值，将 cha[j] 减去该值。

  139. rotate

    不需要去硬算，将数组沿“左上-右下”对角线翻转，然后反转每个一维数组即可。

  140. spiralOrder

    这题用 upper_bound, lower_bound, left_bound 和 right_bound 表示 matrix 的上下左右边界，然后根据这些边界遍历即可。当然遍历完一条边界上的节点就要调整该边界。

  141. generateMatrix

    还上题类似，不过是反着来的。

  142. advantageCount

    田忌赛马问题。原理就是将齐王的马按从大到小的顺序排列，同时记录位置信息，同时将田忌的马从小到大排列，如果田忌最快的马比的过齐王最快的马，那就比，如果比不过，那就派最慢的马去比。

  143. insertdeleteInO(1)

    用 vector 保存数据，用 unordered_map 保存数据的索引，以此达到在 O(1) 空间复杂度内用 O(1) 时间复杂度访问元素。要实现在 O(1) 时间复杂度内增删元素也很简单，将需要删除的元素 swap 到 vector 尾部再删除即可，这时要更新索引。

  144. removeDuplicateLetters

    这题的关键是从字符串 s 中删除一个字符使得 s 的字典序最小。

    这要用到“关键字符”解法：如果 s[i] > s[i+1]，那么删除 s[i]，剩下的字符串就是字典序最小。但是这里又要求所有的字符必须只出现一次，所有要有一个数组记录该字符是否出现过，一个数组记录该字符出现的次数。同时这题还需要使用单调栈。

    先从前向后扫描所有的字符，如果该字符没有访问过，那么对其进行分析，

    • 如果它小于单调栈的栈顶元素，且栈顶元素出现过多次，那么不断将栈顶元素出栈，直到栈顶元素小于该元素；
    • 同时如果栈顶元素只出现 1 次，那么栈顶元素不用出栈；

    否则直接加入单调栈。

  145. exchange

    简单。

  146. replaceSpace

    简单。

  147. getKthFromEnd

    简单。

  148. reverseList

    简单。

  149. isSubStructure

    如何判断 B 是否是 A 的子结构？

    • 判断 B 是否是 A 的子结构 。recur(A, B)
    • 判断 B 是否是 A 左子树的子结构。isSubStructure(A->left, B)
    • 判断 B 是否是 A 右子树的子结构。isSubStructure(A->right, B)

    终止条件：

    if (!B || !A) {
	return false;
}
    bool recur(TreeNode *a, TreeNode *b) {
    if (!b) { // 如果 b 为 null，说明前面匹配
      return true;
    }
    if (!a) { // 如果 a 为 null，说明 a 无法匹配
      return false;
    }
    if (a->val != b->val) { // 没有匹配
      return false;
    }
    // a->val == b->val，递归检查左右子树
    return recur(a->left, b->left) && recur(a->right, b->right);
  }

    对递归的思想还是不熟悉啊。

  150. mirrorTree

    简单。

  151. isSymmetric

    这题很有意思，该问题可以转化为：两个树在什么情况下互为镜像？

    如果同时满足下面的条件，两个树互为镜像：

    • 它们的两个根结点具有相同的值；
    • 每个树的右子树都与另一个树的左子树镜像对称。

    我们可以实现这样一个递归函数，通过**「同步移动」两个指针**的方法来遍历这棵树，pp 指针和 qq 指针一开始都指向这棵树的根，随后 pp 右移时，qq 左移，pp 左移时，qq 右移。每次检查当前 pp 和 qq 节点的值是否相等，如果相等再判断左右子树是否对称。

  152. minStack

    这题用到了辅助栈，min_stack 中保存的是 stack 中从栈底到当前元素的最小值。

  153. validateStackSequences

    比较简单。将 pushed 依次插入栈 s，然后检查 s 中元素是否等于 popped 中的元素，如果等于则将 s 和 popped 的栈顶元素一次出栈。

  154. levelOrder_ii

    复习一下层序遍历。

  155. verifyPostorder

    二叉搜索树的后序遍历的最后一个值就是根节点，而左子树的值都小于根节点，右子树的值都小于根节点，所以可以这样设置递归：

    • 从头遍历，找到第一个大于根节点的值，索引为 m；
    • 继续遍历，确定右子树的值是否都大于根节点，即 p == end；
    • 递归遍历左子树 postorder(start, m - 1)，右子树 postorder(m, end - 1)；

  156. pathSum

    这题我习惯用层序遍历。但是需要加一个队列，用来存储到当前节点为止的路径总和，这个队列的操作和记录节点的队列一样。然后用一个 unordered_map 存储节点的父节点，当 val == target 时逆向遍历该节点的父节点，将它们加入到 res 中。

      vector<vector<int>> pathSum(TreeNode *root, int target) {
    if (!root) {
      return res;
    }

    parent[root] = NULL;
    queue<TreeNode *> q_node;
    queue<int> q_val;
    q_node.push(root);
    q_val.push(0); // 用来记录到当前节点为止的路径总和
    TreeNode *tmp;
    while (!q_node.empty()) {
      tmp = q_node.front();
      int val = tmp->val + q_val.front(); // 这里画个图，结合节点出入队列情况很好理解
      q_node.pop();
      q_val.pop();
      if (tmp->left == NULL && tmp->right == NULL) {
        if (val == target) {
          getPath(tmp);
        }
      } else {
        if (tmp->left) {
          parent[tmp->left] = tmp;
          q_node.push(tmp->left);
          q_val.push(val);
        }
        if (tmp->right) {
          parent[tmp->right] = tmp;
          q_node.push(tmp->right);
          q_val.push(val);
        }
      }
    }
    return res;
  }

  157. copyRandomList

    虽然都是用了 unordered_map，但是题解的方法确实比我简单。

    public:
  Node *copyRandomList(Node *head) {
    if (!head) {
      return NULL;
    }

    unordered_map<Node *, Node *> m;
    Node *p = head;
    // 第一次遍历只原节点对应的复制节点
    while (p) {
      m[p] = new Node(p->val);
      p = p->next;
    }

    Node *q = head;
    while (q) {
      m[q]->next = m[q->next]; // 这里很巧妙
      m[q]->random = m[q->random];
      q = q->next;
    }
    return m[head];
  }

  158. treeToDoublyList

    比较简单，中序遍历即可。要注意只有一个节点时，其左右指针指向本身。

  159. majorityElement

    简单。

  160. getLeastNumbers

    sort 的使用：

    sort(arr.begin(), arr.end(), less<int>());

  161. findMedian

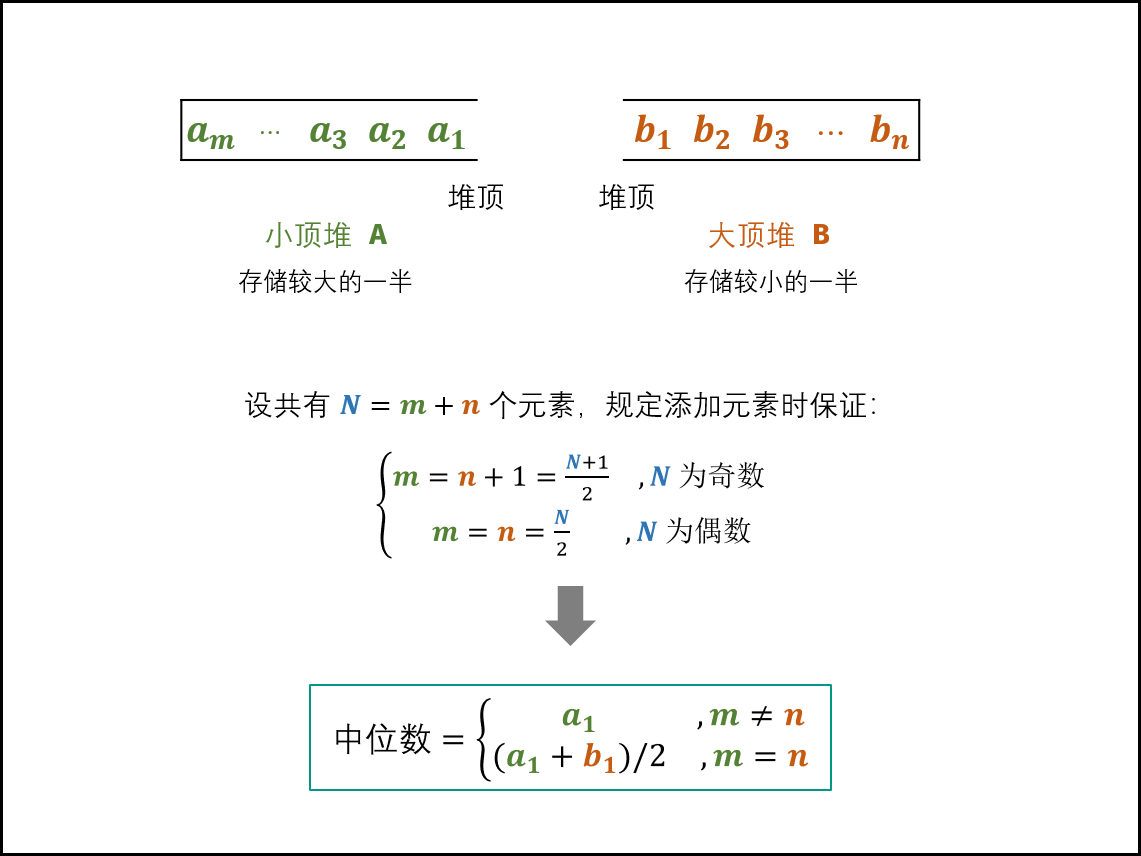
    这题要用到两个 priority_queue，

    // store the less numbers, the top is the largest in this region.
priority_queue<int, vector<int>, less<int>> max_q;
// store the greater numbers, the top is the smallest in this region.
priority_queue<int, vector<int>, greater<int>> min_q;

    这个图很形象，但是和我写的代码不完全相同。max_q 是大顶堆，用于更小的那部分数据，min_q 是小顶堆，用于保存更大的那部分数据。而当向堆中插入数据时，为了保证左边的数据始终小于右边的数据和右边的数据始终大于左边的数据，所以不能直接往左右两个堆中插入数据，而是先向 max_q 插入，这时 max_q 栈顶保存就是该部分最大的那个值，将栈顶元素再插入 min_q。往右边插也是这样的。

  162. countDigitOne

    题目看起来简单，但没想对思路很难做出来。这篇题解写的很清楚。这里的笔记是我自己对题解的理解。

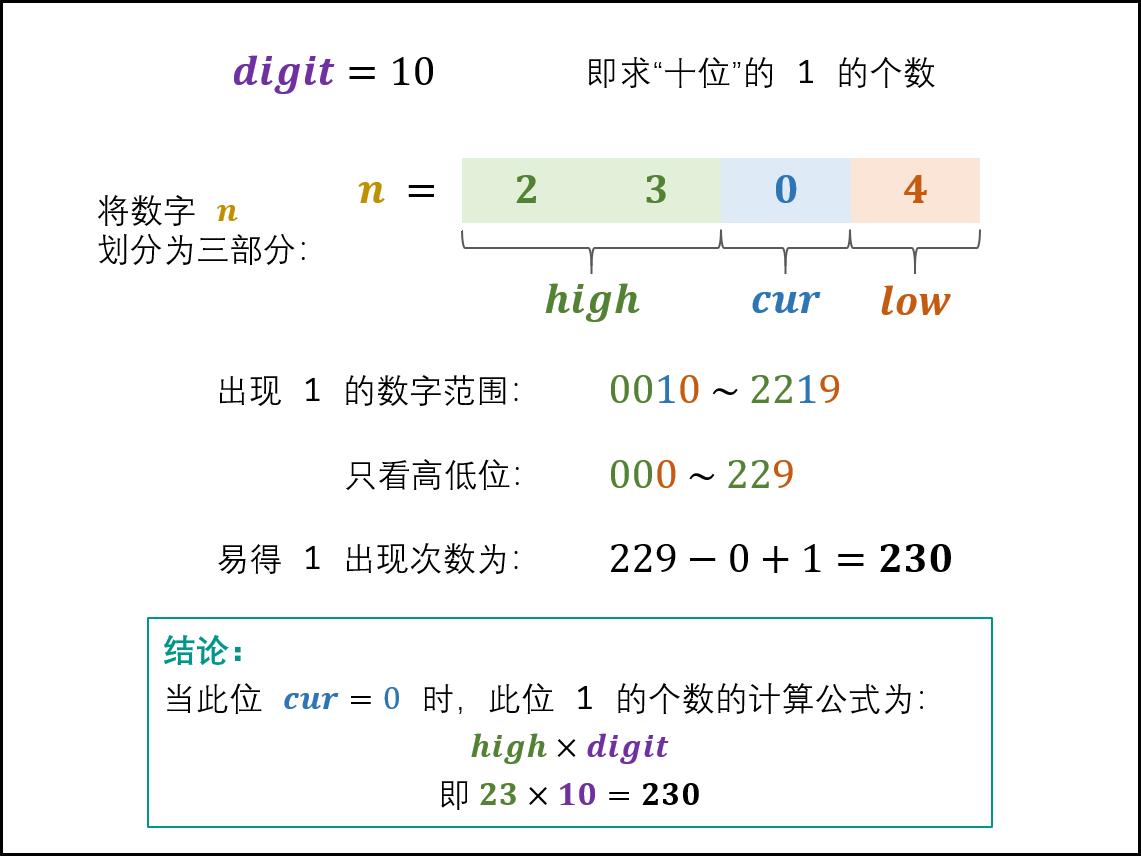
    将 n 分成 high, cur, low，

    • cur = 0

      cur 位上出现 1 的次数取决于 high，res = high * digit

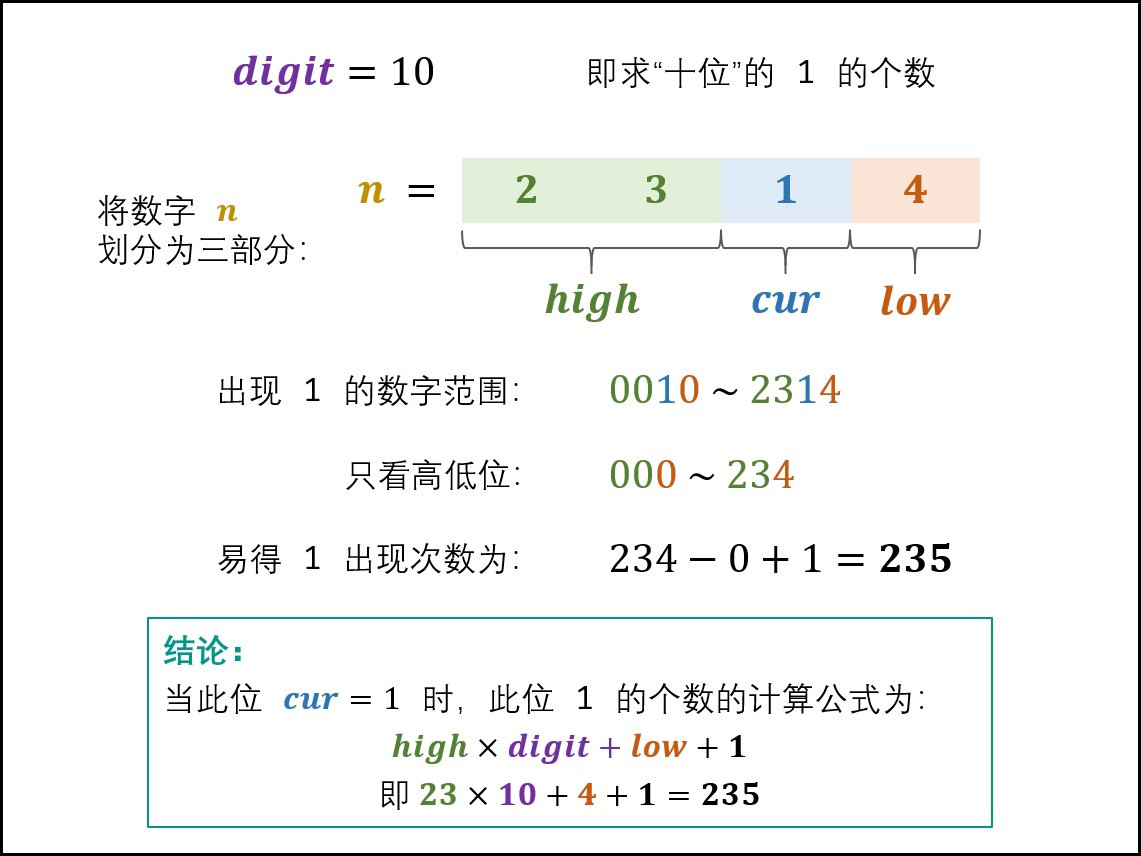
    • cur = 1

      cur 位上出现 1 的次数取决于 high 和 low，res = high * digit + low + 1

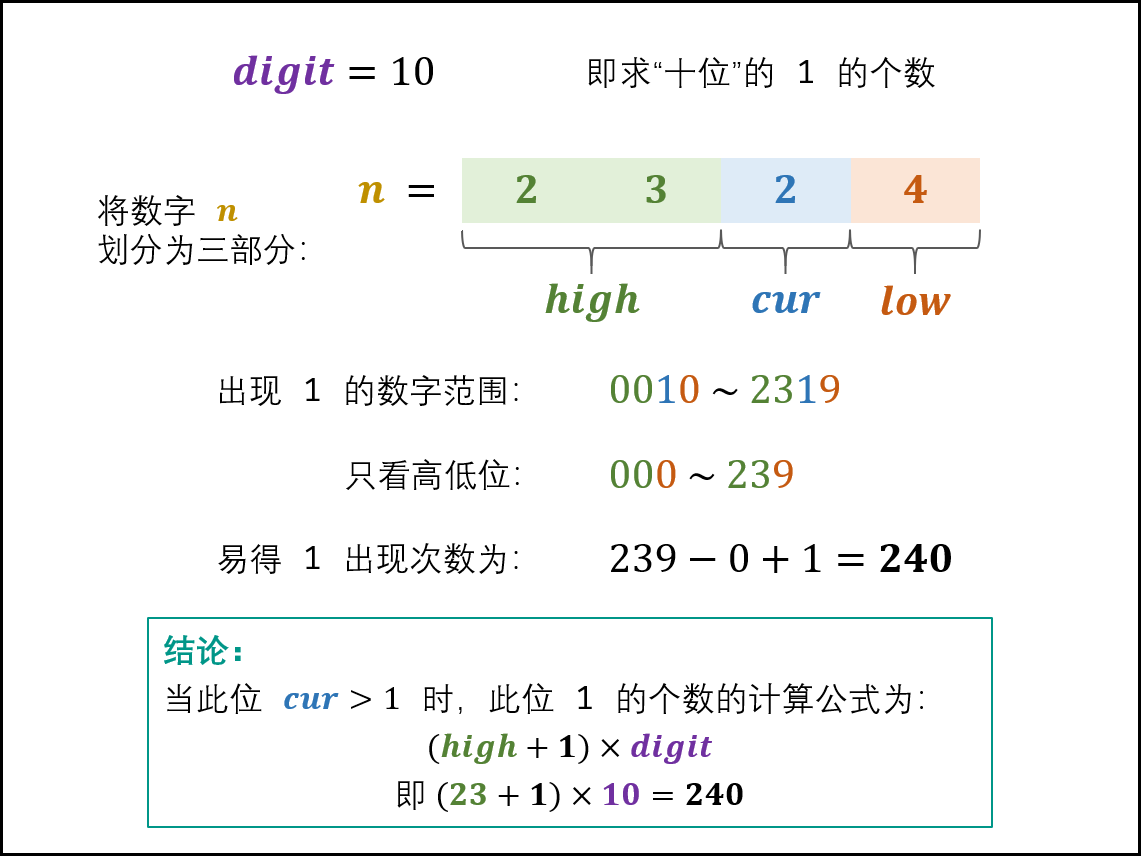
    • cur = 2 ~ 9

      cur 位上出现 1 的次数取决于 high，res = (high + 1) * digit

  163. findNthDigit

    这题不难。

    按照数字的位数计算 n 对应的是哪个数字，例如如果 10 <= n < 190，那么 n 对应的一定是两位数，减去个位数占的位数，就可以得出 n 对应的是哪个两位数，再计算是该两位数的哪一位。

    	if (n < 10) { // 0 ~ 9
      res = n;
    } else if (n < 190) { // 10 ~ 99
      n -= 10;
      num = 10 + n / 2;
      digit = n % 2;
      digit = 1 - digit;
      while (digit >= 0) {
        res = num % 10;
        num /= 10;
        digit--;
      }
   }

  164. minNumber

    这题主要是字符串排序，我们可以使用 STL 中的 sort，然后自定义 compare 函数。

    static bool compare(const string &s1, const string &s2) {
    string ab = s1 + s2;
    string ba = s2 + s1;
    return ab < ba; // '303` is larger than '330`
}

    需要记住这种 compare 的写法。

  165. translateNum

    这题和 3. climbStairs 做法一样，使用动态规划，因为可以选择是一个字符还是两个字符组合，但是两个字符组成的数字不能超过 25，所以要添加一个判断条件，

    	for (int i = 2; i < size; i++) {
      s2 = stoi(s.substr(i - 1, 2));
      if (s2 > 25 || stoi(s.substr(i - 1, 1)) == 0) {
        dp[i] = dp[i - 1];
      } else {
        dp[i] = dp[i - 1] + dp[i - 2];
      }
    }

  166. maxValue

    典型的动态规划问题。

    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];

  167. firstUniqChar

    简单，用 unordered_map 和 vector 都可以。

  168. getIntersectionNode

    简单。用一个哈希表 unordered_map 存储 A 链表，然后遍历 B 链表，看 unordered_map 中是否存在即可。

  169. kthLargest

    简单，中序遍历即可。

  170. singleNumber

    先做的下一题，这题看起来就顺眼多了。

  171. singleNumbers

    真是妙蛙种子吃着妙脆角妙进了米奇妙妙屋，妙到家了。

    这题用到“异或”操作，两个相同的数“异或”结果为 0，不同的数“异或”结果为两数之和。对 nums 中所有的数进行“异或”操作，因为只有两个数不同，所有最后的结果就是这两数之和。

    我们对这个结果进行分析，将这个结果转化为二进制数，如果二进制中的位为 “1”，说明两个不同的数这一位不同，我们就选择这个不同的位，将 nums 中所有的数字分成两组，那么相同的数字必定被分到同一组，因为相同的数字二进制表示中所有的位都相同，而目标两个不同的数字必定被分到不同的组，再对这两个组进行“异或”操作，那么就可以得到目标结果。

    	for (int i = 0; i < n; i++) {
      tmp ^= nums[i];
    }
    int div = 1;
    while ((div & tmp) == 0) {
      div <<= 1;
    }

    for (int i = 0; i < n; i++) {
      if ((nums[i] & div) == 0) {
        res[0] ^= nums[i];
      } else {
        res[1] ^= nums[i];
      }
    }

  172. singleNumbers_ii

    好吧，这题不用那么复杂的算法，直接 unordered_map 即可。

  173. findContinuousSequence

    复习一下双指针。检查 nums[left, right] 中元素和是否等于 target。如果大了，left++，同时临时数组的 left 也要删除；如果小了，right++。

  174. maxQueue

    我还想用 164. minStack 一样的方法，设个辅助队列来求，没想到直接暴力法就可以。

  175. isStraight

    比较简单，找到所有的 0，然后计算 0 的数量够不够“填洞”。

  176. lastRemaining

    “约瑟夫环”问题，具体分析过程很复杂，暂时不去理解，好在代码简单。

      int lastRemaining(int n, int m) {
    int res = 0;
    for(int i = 2; i <= n; i++){
      res = (res + m) % i;
    }
    return res;
  }

  177. sumNums

    这题主要的限制是不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句（A?B:C）。所以使用递归的方式来计算和，但是递归要有一个终止条件，一般是用 if() 来判断，但是题目要求不能使用，所以这里使用了位运算符的短路性质。

      int sumNums(int n) {
    bool x = (n > 1 && sumNums(n - 1));
    res += n;
    return res;
  }

    如果 n <= 1 的话后面就不会执行了。

  178. add

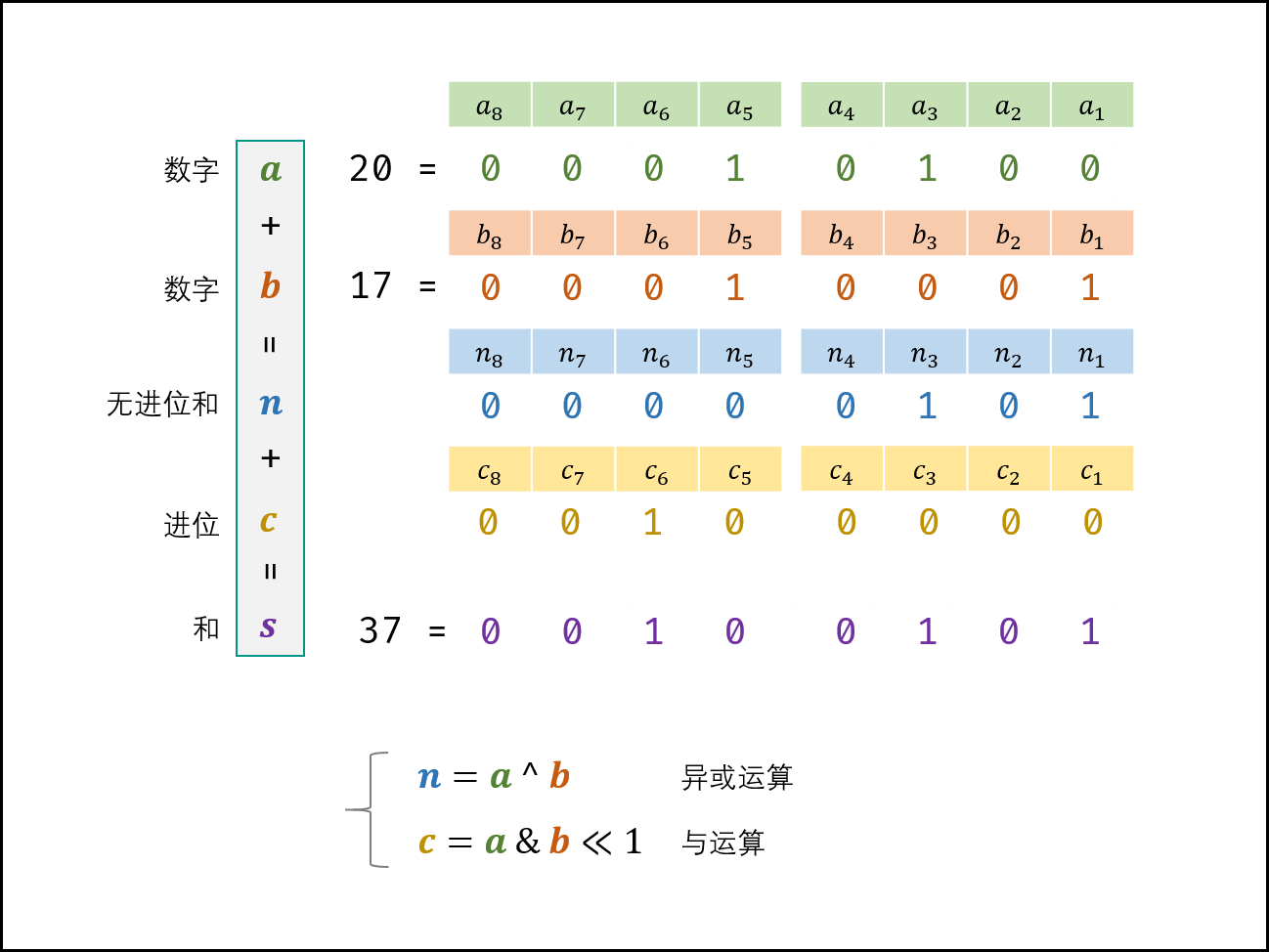
    这是让我们理解计算机是怎样做加法的，我们看这张图更加清楚。

    这里需要注意负数不能直接移位，需要转换为无符号整型。

  179. constructArr

    看一下这个图就明白了，

  180. strToInt

    题目不难，但是要多测几次，以判断各种情况。

  181. addBinary

    题目不难，分类处理即可。

    	while (--na >= 0) {
      if (a[na] == '0' && b[na] == '0' && carry == '0') {
        res.insert(res.begin(), '0');
        carry = '0';
      } else if ((a[na] == '0' && b[na] == '0' && carry == '1') ||
                 (a[na] == '0' && b[na] == '1' && carry == '0') ||
                 (a[na] == '1' && b[na] == '0' && carry == '0')) {
        res.insert(res.begin(), '1');
        carry = '0';
      } else if ((a[na] == '0' && b[na] == '1' && carry == '1') ||
                 (a[na] == '1' && b[na] == '0' && carry == '1') ||
                 (a[na] == '1' && b[na] == '1' && carry == '0')) {
        res.insert(res.begin(), '0');
        carry = '1';
      } else if ((a[na] == '1' && b[na] == '1' && carry == '1')) {
        res.insert(res.begin(), '1');
        carry = '1';
      }
    }
    if (carry == '1') {
      res.insert(res.begin(), carry);
    }

  182. countBits

    还是使用动态规划。

    for (int i = 1; i <= n; i++) {
  res[i] = res[i >> 1] + i % 2;
}

  183. maxProduct_ii

    位运算的妙用啊！用一个 int 类型的二进制位的每一位表示某个字母是否出现，如 0x111 表示该字符串为 abc，然后对每个字符串的 mask 进行“与”操作，结果为 0 说明没有重复的字母出现。

      for (int i = 0; i < n; i++) {
      for (int j = 0; j < (int)words[i].size(); j++) {
        mask[i] |= 1 << (words[i][j] - 'a'); // 该字母是否出现
      }
  }

  184. minSubArrayLen

    典型的双指针。

  185. numSubarrayProductLessThanK

    还是用双指针，

        while (right < n) {
      product *= nums[right];
      while (left <= right && product >= k) {
        product /= nums[left];
        left++;
      }
      res += right - left + 1; // 这个地方需要理解
      right++;
    }

    以 [10,5,2,6] 分析，

    • 当 left = 0, right = 0 时

      res += 1，即 10

    • 当 left = 0, right = 1 时

      res += 2，即 5, 10, 5

    • 当 left = 1, right = 2 时

      res += 2，即 5, 2, 2

    • 当 left = 1, right = 3 时

      res += 3，即 2,6, 6, 5,2,6

  186. pivotIndex

    简单题，用位运算加快速度。

  187. findMaxLength

    这题使用前缀和。将 0 转换成 -1，那么题目就可以转换成“和为 0 的最长连续子数组“，我们使用哈希表 m 存储数组到当前索引时“前缀和”和“索引”之间的映射，一个 count 表示数组当前索引下的前缀和，如果 m[count] != 0 说明该前缀和已经出现过，那么 i - m[count] 就是一个和为 0 的连续子数组。

        for (int i = 0; i < n; i++) {
      if (nums[i]) {
        count++;
      } else {
        count--;
      }
      if (m.count(count)) {
        res = max(res, i - m[count]);
      } else {
        // if m.count(count) != 0,
        // m[count] is smallest, so we don't need update it.
        m[count] = i;
      }
    }

    同时我们需要设置 m[0] = -1，即初始化前缀和为 0 的子数组索引为 -1。我们以 [0,1,0] 为例，当索引值为 1 时，count = 0，i - m[count] = 2，子数组为 [0,1]。

  188. sumRegion

    还是使用前缀和，这里看图就明白了。

    sumRegion.png

          for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
          sum[i + 1][j + 1] =
              sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
        }
      }
      int sumRegion(int row1, int col1, int row2, int col2) {
    return sum[row2 + 1][col2 + 1] - sum[row2 + 1][col1] - sum[row1][col2 + 1] +
           sum[row1][col1];
  }

  189. getProduct

    比较简单，还是使用前缀和，但是要注意如果有一个数为 0，那么所有的前缀和都要为 0。

  190. validPalindrome

    简单。在遇到不同的字符时分成 s[left + 1, right] 和 s[left, right + 1] 判断。

  191. countSubstrings

    这题可以用动态规划来做。

    状态转移方程：

    		if (s[left] == s[right] &&
            ((right - left < 2) || dp[left + 1][right - 1])) {
          dp[left][right] = 1;
        }

    也就是说如果 s[left] == s[right]，那么 dp[left] [right] = dp[left + 1] [right - 1]，这个很好理解；如果 right - left < 2，如 aa 也是回文。

  192. removeNthFromEnd

    这题要求遍历一次删除倒数第 n 个节点，可以使用双指针，first 向前遍历 n 个节点后 second 开始遍历，这样 first 遍历完后 second 指向的就是倒数第 n 个节点。

  193. addTwoNumbers_ii

    这题用栈确实更简单，然后不断将结果插入到链表头。

  194. reorderList

    先利用快慢指针找到中间节点，然后断开成俩部分，后半段完成翻转，然后与前半段进行合并。

      void reorderList(ListNode *head) {
    if (!head || !head->next) {
      return;
    }
    ListNode *one = head;
    ListNode *two = head->next;
    // find middle node
    while (two && two->next) {
      two = two->next->next;
      one = one->next;
    }

    // reverse the latter part
    ListNode *prev = NULL;
    ListNode *cur = one->next;
    ListNode *next;
    // disconnect front part and latter part
    one->next = NULL;
    while (cur) {
      next = cur->next;
      cur->next = prev;
      prev = cur;
      cur = next;
    }

    // merge two list
    ListNode *first = head;
    ListNode *second = prev;
    ListNode *first_next;
    ListNode *second_next;
    while (first && second) {
      first_next = first->next;
      second_next = second->next;
      first->next = second;
      second->next = first_next;
      first = first_next;
      second = second_next;
    }
  }

    关于链表的一些编程习惯要改，以上面的为准。

  195. insert_ii

    这种链表的题目思路不难，但是要调整细节就很麻烦，花时间。

  196. isAnagram

    简单。

  197. groupAnagrams

    这题的“变位词”定义和上一题的不一样。若两个字符串中每个字符出现的次数都相同，则称它们互为变位词。那么将其按字母序排序后互为变位词的两个词应该是一样的。

    我们将排序后的字符串作为 key，将 strs[i] 作为值存入 unordered_map<string, vector<string>> m; 即可。

  198. findMinDifference

    比较简单。将时间转化为 int 类型，然后再比较，注意最后一个时间和第一个时间的比较。

  199. evalRPN

    将一个普通的中缀表达式转换为逆波兰表达式的一般算法是：

    首先需要分配 2 个栈，一个作为临时存储运算符的栈 S1（含一个结束符号），一个作为存放结果（逆波兰式）的栈 S2（空栈），S1 栈可先放入优先级最低的运算符 #，注意，中缀式应以此最低优先级的运算符结束。可指定其他字符，不一定非 # 不可。从中缀式的左端开始取字符，逐序进行如下步骤：

    （1）若取出的字符是操作数，则分析出完整的运算数，该操作数直接送入 S2 栈。

    （2）若取出的字符是运算符，则将该运算符与 S1 栈栈顶元素比较，如果该运算符(不包括括号运算符)优先级高于 S1 栈栈顶运算符（包括左括号）优先级，则将该运算符进 S1 栈，否则，将 S1 栈的栈顶运算符弹出，送入 S2 栈中，直至 S1 栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入 S1 栈。

    （3）若取出的字符是“（”，则直接送入 S1 栈顶。

    （4）若取出的字符是“）”，则将距离 S1 栈栈顶最近的“（”之间的运算符，逐个出栈，依次送入 S2 栈，此时抛弃“（”。

    （5）重复上面的 1~4 步，直至处理完所有的输入字符。

    （6）若取出的字符是“#”，则将 S1 栈内所有运算符（不包括“#”），逐个出栈，依次送入 S2 栈。

    完成以上步骤，S2 栈便为逆波兰式输出结果。不过 S2 应做一下逆序处理。便可以按照逆波兰式的计算方法计算了！计算方法如下。

    逆波兰表达式严格遵循「从左到右」的运算。计算逆波兰表达式的值时，使用一个栈存储操作数，从左到右遍历逆波兰表达式，进行如下操作：

    • 如果遇到操作数，则将操作数入栈；

    • 如果遇到运算符，则将两个操作数出栈，其中先出栈的是右操作数，后出栈的是左操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数入栈。

    整个逆波兰表达式遍历完毕之后，栈内只有一个元素，该元素即为逆波兰表达式的值。

  200. calculate

    总体的流程就是上面的，但是最后一个例子超时了，思路是正确的。

  201. asteroidCollision

    需要注意删除爆炸小行星后的索引值。

  202. movingAverage

    简单。

  203. CBTInserter

    层序遍历的应用。额外使用一个队列 queue<TreeNode *> ql; 用来记录从第一个左/右子树为空的节点—— location 之后的所有节点。

    	  // reocrd nodes after the first suitable node
      if (!p->left || !p->right) {
        ql.push(p);
      }

    而第一个左/右子树为空的节点就是可以插入的节点，在插入新节点后，需要更新 location，

      int insert(int v) {
    TreeNode *p = location;
    if (!p->left) {
      p->left = new TreeNode(v, NULL, NULL);
      ql.push(p->left);
      // update location
      location = p;
      return p->val;
    } else if (!p->right) {
      p->right = new TreeNode(v, NULL, NULL);
      ql.push(p->right);
      // we need pop the top node, because it already has left child and right
      // child.
      ql.pop();
      location = ql.front();
      return p->val;
    } else {
      return -1;
    }
  }

  204. largestValues

    层序遍历的应用，简单。

  205. findBottomLeftValue

    层序遍历的应用，简单。

  206. pruneTree

    二叉树的递归。这种题目遇到很多次了，但对递归的思想始终不清楚。这题能很好的解释。

    其实二叉树的递归无非是前序、中序和后序，需要知道递归返回的条件和不同序列对应的操作。这里判断节点本身的值是否为 1 和左右子树中是否含有值为 1 的节点。所以需要的操作很简单，

      bool isContain(TreeNode *root) {
    if (!root) {
      return false;
    }
    bool left = isContain(root->left);
    bool right = isContain(root->right);
    if (!left) {
      root->left = NULL;
    }
    if (!right) {
      root->right = NULL;
    }
    return (root->val == 1) || left || right; // 判断本身和左右子树
  }

  207. sumNumbers

    经典的二叉树递归。在左右子树遍历完后要将加入 string order; 中的值去除。

  208. pathSum_ii

    和 168. pathSum 有点类似，不过不是计算整条路径的和，而是计算任意一条路径，那么我们在遍历每个节点时都计算该节点到根节点的子路径和，这里通过一个 unordered_map<TreeNode *, TreeNode *> parent; 记录某个节点的父节点。

  209. maxPathSum

    思路是正确的，但是在取最大值上还有问题。递归的计算左右子树的值，

    int left = max(calculate(root->left), 0); // 只有该子树的值大于 0 才能参与计算最大值，不然相加肯定小于最大值
int right = max(calculate(root->right), 0);

    更新最大值，

    res = max(left + right + root->val, res);

    返回该节点和左子树/右子树的和，

    return max(left, right) + root->val;

  210. increasingBST

    简单。

  211. MyCalendar

    简单。

  212. KthLargest

    使用一个大小为 k 的优先队列来存储前 k 大的元素，其中优先队列的队头为队列中最小的元素，也就是第 k 大的元素。

    在单次插入的操作中，我们首先将 val 加入到优先队列中。如果此时优先队列的大小大于 k，我们需要将优先队列的队头元素弹出，以保证优先队列的大小为 k。

  213. topKFrequent

    经典的优先级队列的应用，

    	struct compare {
      bool operator()(pair<int, int> &a, pair<int, int> &b) {
        return a.second > b.second; // the less element is in top
      }
    };

    priority_queue<pair<int, int>, vector<pair<int, int>>, compare> pq;
    for (auto m : map) {
      pq.push(m);
      if ((int)pq.size() > k) {
        pq.pop();
      }
    }

    这题要多复习几遍。关于优先级队列的介绍可以看这里。

  214. kSmallestPairs

    还是优先级队列，不过这题的使用方法我不懂。

        auto compare = [&nums1, &nums2](const pair<int, int> &a,
                                    const pair<int, int> &b) {
      return nums1[a.first] + nums2[a.second] >
             nums1[b.first] + nums2[b.second];
    };

    priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(compare)>
        pq(compare);

    然后关于这题的解法也有些需要注意的。前 k 对最小的数对，我们先在优先级队列中放入 [0,0]、[1, 0]、[2, 0]、…… ，这里 [0,0] 表示数对 nums1[0], nums2[0]，即让 nums2 的索引全部从 0 开始，每次弹出 nums1[index1] + nums2[index2] 较小者。弹出之后，再把 index2 后移一位继续添加到优先级队列中，依次往复，最终弹出 k 次就是我们的结果。更加详细的解释可以看这里。

  215. isSubtree

    前序遍历的应用，每个节点都通过 isSame 判断一下以该节点为根节点的树是否和 subRoot 一样，

      bool isSame(TreeNode *a, TreeNode *b) {
    if (a == NULL && b == NULL) {
      return true;
    }
    if (a == NULL || b == NULL) {
      return false;
    }
    if (a->val != b->val) {
      return false;
    }
    return isSame(a->left, b->left) && isSame(a->right, b->right);
  }

  216. isCousins

    我还是喜欢用层序遍历来求树的高度。

  217. findSecondMinimumValue

    比较简单，用堆来动态存储前 n 小（大）的值。

  218. pathInZigZagTree

    这题主要是数学公式。正常的完全二叉树中第 n 个节点的父节点是 n/2，而这里需要做个转换。

    	while (label >= 1) {
      res.insert(res.begin(), label);
      label /= 2;

      int depth = (int)(log(label) / log(2));
      // label - pow(2, depth) 求出该节点是该层的第几个
      label = pow(2, depth + 1) - 1 - (label - pow(2, depth));
    }

  219. findTilt

    简单，但对这种思想的应用还需加强。

  220. tree2str

    还需加强。

  221. distanceK

    这题做法很巧妙，将以 root 为根节点的二叉树转化为以 target 为根节点的多叉树，只要加上一个 parent 信息就行，然后再用多叉树的层序遍历即可。注意要加上一个 visited，因为需要遍历 parent 会导致重复遍历。

  222. sumRootToLeaf

    和 168. sumNumbers 一样，不过要修改一下计算和的函数。

  223. verticalTraversal

    前序遍历的应用，需要记录节点的坐标，所以用的结构体比较复杂，

    unordered_map<int, vector<vector<int>>> m;
m[column].push_back({row, root->val});

    之后就是将数据按照题目要求的方式排列，

    	vector<vector<int>> tmpvv;
    for (int i = start; i <= end; i++) {
      tmpvv = m.find(i)->second;
      sort(tmpvv.begin(), tmpvv.end(), cmp);
      vector<int> tmpv;
      for (auto v : tmpvv) {
        tmpv.push_back(v[1]);
      }
      res.push_back(tmpv);
    }

    这里因为要求“按列索引每一列上的所有结点，形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，则按结点的值从小到大进行排序，”所以还写了个 cmp 函数，

    static bool cmp(vector<int> a, vector<int> b) {
    if (a[0] == b[0]) {
      return a[1] < b[1];
    }
    return a[0] < b[0];
  }

    没什么特别的，就是要加个 static。

  224. trimBST

    说实话，不理解。

  225. consecutiveNumbersSum

    我的方法能写出来，但是超时了。

  226. numDecodings

    和 177. translateNum 类似，不过这里不能有前缀 0，所以需要考虑的情况多一些，

    	for (int i = 2; i < n; i++) {
      if (s[i] == '0') {
        if (s[i - 1] == '0') {
          return 0;
        }
        if (stoi(s.substr(i - 1, 2)) > 26) {
          return 0;
        }
        dp[i - 1] = dp[i - 2];
        dp[i] = dp[i - 1];
      } else if (stoi(s.substr(i - 1, 2)) > 26 || s[i - 1] == '0') {
        dp[i] = dp[i - 1];
      } else {
        dp[i] = dp[i - 1] + dp[i - 2];
      }
    }

  227. uniquePaths

    简单的动态规划。

  228. uniquePathsIII

  229. minPathSum

    简单的动态规划。

  230. canJump

    这题不要用动态规划，直接遍历一遍就行，将能够够得着的值置为’1‘，然后检查最后一个的元素的值是否为’1‘。

  231. jump

    这题跟前面的 2. coinChange 和 3. climbStairs 有相似之处，但又不完全一样。它需要动态的判断能够跳到哪里，比如第 1 次最远能跳 2 步，那就检查这 2 步哪一步能跳的距离最远，

    	for (int i = 0; i < n - 1; i++) {
      fast = max(fast, nums[i] + i);
      if (end == i) { // 2 步结束，更新下一步能跳的最远距离
        res++;
        end = fast;
      }
    }

  232. generate

    比较简单。

  233. getRow

    和上题一样。

  234. uniquePathsWithObstacles

    和 238. uniquePaths 类似，不过要加上一些判断条件，如果该节点是障碍节点，那么路径数为 0，然后每次递增时都要判断左边的节点和上面的节点是否为障碍节点。

        for (int i = 1; i < m; i++) {
      for (int j = 1; j < n; j++) {
        if (obstacleGrid[i][j]) {
          dp[i][j] = 0;
          continue;
        }
        if (obstacleGrid[i][j - 1] && obstacleGrid[i - 1][j] == 0) {
          dp[i][j] = dp[i - 1][j];
        } else if (obstacleGrid[i - 1][j] && obstacleGrid[i][j - 1] == 0) {
          dp[i][j] = dp[i][j - 1];
        } else if (obstacleGrid[i - 1][j] == 0 && obstacleGrid[i][j - 1] == 0) {
          dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        } else {
          dp[i][j] = 0;
        }
      }
    }

  235. wordBreak

    状态转移方程：

    dp[i]=dp[j] && check(s[j..i−1])

    check(s[j..i−1]) 表示 s[j..i-1] 是否在 word 中，

    	for (int i = 1; i <= m; i++) {
      for (int j = 0; j < i; j++) {
        if (dp[j] && map[s.substr(j, i - j)] == 1) {
          dp[i] = 1;
          break;
        }
      }
    }

  236. longestValidParentheses

    用这种方式判断括号串是否合法，

    	for (int i = 0; i < n; i++) {
      if (s[i] == '(') { // 如果是 '(' 将 index 入栈
        stk.push(i);
      } else {
        if (!stk.empty()) { // 如果是 ')'，那么直接和栈顶的 '(' 匹配，计算长度
          tmp = stk.top();
          stk.pop(); // 栈里只有 '('
          len = i - tmp + 1;
        } else {
          // 没有匹配的‘)’，直接跳过或出错
        }
      }
    }

    然后用 dp[i] 表示到 s[i - 1] 为止有效括号的长度，所以最后的算法是这样的，

        for (int i = 0; i < n; i++) {
      if (s[i] == '(') {
        stk.push(i);
        dp[i + 1] = 0;
      } else {
        if (!stk.empty()) {
          tmp = stk.top();
          stk.pop();
          len = i - tmp + 1 + dp[tmp];
          dp[i + 1] = len;
        } else {
          dp[i + 1] = 0;
        }
      }
    }

    以 '()()()' 为例，遍历完第一个 '()' 后，dp[2] = 2，继续遍历下一个 '()' 时，'(' 的索引是 2，所以能够加上。

  237. canPartition

    md，差点得了图灵奖，

    本题是经典的「NP 完全问题」，也就是说，如果你发现了该问题的一个多项式算法，那么恭喜你证明出了 P=NP，可以期待一下图灵奖了。

    所以双指针解不出来。

    还是用动态规划，不过我想不出来。

    首先确定状态转移方程：dp[i][j] 表示在 nums[0..i] 中是否能够选取几个数字（包括 0 个）使得其和为 j，那么就有两种情况：

    • j < nums[i]，那么 nums[i] 就不能加入讨论，所以 dp[i][j] = dp[i - 1][j];
    • j >= nums[i]，那么 nums[i] 能够加入讨论，dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];

    然后确定 dp base：

    • 当 i = 0 时，那么无法选择任何数字，dp[0][j] = 0；
    • 当 j = 0 时，那么 dp[0][0] = 1；
        // dp[i][j] present if there is a solution that choose some numbers
    // (include 0 number) from nums[0, i] and the sum is equal j.
    vector<vector<bool>> dp(n + 1, vector<bool>(sum + 1, false));
    // for (int i = 0; i <= n; i++) {
    // dp[i][0] = true; // we can choose 0 number and the sum is always 0.
    // }
    // dp[0][nums[0]] = true; // we can only choose nums[0].
    dp[0][0] = true;

    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= sum; j++) {
        if (j < nums[i - 1]) {
          // nums[i] should not add, because nums[i] is larger than sum(j),
          // so dp[i][j] must be false if nums[i] add.
          dp[i][j] = dp[i - 1][j];
        } else {
          // nums[i] is smaller than sum(j), so if we add nums[i], dp[i][j]
          // equals dp[i -1][j - nums[i]], if we don't add, dp[i][j] equals
          // dp[i- 1][j].
          dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i - 1]];
        }
      }
    }

    这道题还要多做几次。

    暴力回溯也能做，不过会超时。

  238. findTargetSumWays

    这题和上题类似，我们先转化一下，向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，使得构造的表达式和为 target，我们假设添加 - 的数字的和为 neg，则

    sum - neg - neg = target -> neg = (sum - target) / 2

    也就是说要求数组中和为 neg 的子数组，那么就和上题类似。

    确定状态转移方程：dp[i][j] 表示在 nums[0..i] 中选取几个数字（包括 0 个），使得其和为 j 的情况数，那么就有两种情况：

    • j < nums[i]，那么 nums[i] 就不能加入讨论，所以 dp[i][j] = dp[i - 1][j];
    • j >= nums[i]，那么 nums[i] 能够加入讨论，dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];

    然后确定 dp base：

    • 当 i = 0 时，那么无法选择任何数字，dp[0][j] = 0；
    • 当 j = 0 时，那么 dp[0][0] = 1；

  239. maximalSquare

    简单的动态规划，

    首先确定状态转移方程：dp[i][j] 表示 matrix[i][j] 最大的正方形面积

    • matrix[i][j] = '1': dp[i][j] = (min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1) ^ 2；
    • matrix[i][j] = '0': dp[i][j] = 0；

    dp base：

    • dp[0][i] = matrix[0][i] - '0';
    • dp[i][0] = matrix[i][0] - '0';

    最后返回最大

  240. combinationSum

    回溯法，对于细节的调试还需要更加熟练，才能快速写出来。

  241. combinationSum_ii

    上一题一样，只不过每个数字只能使用一次，所以

    	for (int i = start; i < end; i++) {
      if (i > start && candidates[i] == candidates[i - 1]) {
        continue; // 为了去除重复情况，加上一个判断
      }
      sum += candidates[i];
      tmp.push_back(candidates[i]);
      backtrace(tmp, sum, i + 1, end); // 从 i + 1 开始递归
      tmp.pop_back();
      sum -= candidates[i];
    }

  242. combinationSum_iii

    简单的回溯法，和前面两题类似。

  243. solveSudoku

    就是穷举，判断 1 ~ 9 是否合适，合适就判断下一个。

      bool backtrace(vector<vector<char>> &board, int i, int j) {
    int m = 9, n = 9;
    if (j == n) { // the last column
      return backtrace(board, i + 1, 0);
    }
    if (i == m) {
      // this is a solution
      return true;
    }

    if (board[i][j] != '.') {
      // this space has number
      return backtrace(board, i, j + 1);
    }

    for (char ch = '1'; ch <= '9'; ch++) {
      // check every number
      if (!isVaild(board, i, j, ch)) {
        continue;
      }
      board[i][j] = ch;
      // 合适，判断下一个，如果下一个返回 false，遍历下一个字符看是否合适
      if (backtrace(board, i, j + 1)) {
        return true;
      }
      board[i][j] = '.';
    }
    return false;
  }
      bool isVaild(vector<vector<char>> &board, int r, int c, char ch) {
    for (int i = 0; i < 9; i++) {
      if (board[r][i] == ch) {
        return false;
      }
      if (board[i][c] == ch) {
        return false;
      }
      if (board[(r / 3) * 3 + i / 3][(c / 3) * 3 + i % 3] == ch) {
        return false;
      }
    }
    return true;
  }

  244. canPartitionKSubsets

    这题的做法就是暴力遍历，增加一个 used 变量利用位操作记录对应的数字是否使用。

      bool backtrace(int k, int bucket, int target) {
    if (k == 0) {
      return true;
    }
    if (bucket == target) {
      return backtrace(k - 1, 0, target);
    }

    for (int i = 0; i < (int)nums.size(); i++) {
      if (used & (1 << i)) { // this number has been used
        continue;
      }
      if (bucket + nums[i] > target) {
        continue;
      }
      bucket += nums[i];
      used |= (1 << i);
      if (backtrace(k, bucket, target)) {
        return true;
      }
      used ^= (1 << i);
      bucket -= nums[i];
    }
    return false;
  }

    不过暴力法我也不熟练啊。

  245. wordBreak_ii

    直接回溯，比较简单。

  246. slidingPuzzle

    这题确实很难，巧妙的使用 BFS。首先要将 vector<vector<int>> board 转化成 string，便于时用哈希表记录该种情况是否出现过。

        string init;
    for (int i = 0; i < 2; i++) {
      for (int j = 0; j < 3; j++) {
        init.push_back(board[i][j] + '0');
      }
    }

    然后记录某个块的所有相邻块，这些都是可以交换的，

        vector<vector<int>> neighbor = {{1, 3}, {0, 2, 4}, {1, 5},
                                    {0, 4}, {1, 3, 5}, {2, 4}};

    所谓 BFS 就是找到 ’0‘ 即空白的块，然后和相邻块交换，将交换后得到的序列如栈，如果哈希表中该序列没有出现，

            int location = tmp.first.find('0');
        for (int j = 0; j < (int)neighbor[location].size(); j++) {
          swap(tmp.first[location], tmp.first[neighbor[location][j]]);
          string str = tmp.first;
          if (map[tmp.first] != 1) {
            q.push({str, res + 1});
            map[str] = 1;
          }
          swap(tmp.first[location], tmp.first[neighbor[location][j]]);
        }

    再结合 BFS 的框架就行了。

  247. openLock

    好吧，这题虽说也是直接遍历，但是我写不出来。关键还是理解 BFS，这里需要注意一个状态转动一次能够到达的状态，

            for (int j = 0; j < 4; j++) {
          string tmp1 = up(str, j);
          if (visited[tmp1] != 1) {
            q.push(tmp1);
            visited[tmp1] = 1;
          }

          string tmp2 = down(str, j);
          if (visited[tmp2] != 1) {
            q.push(tmp2);
            visited[tmp2] = 1;
          }
        }
      string up(string str, int location) {
    if (str[location] == '9') {
      str[location] = '0';
    } else {
      str[location] = str[location] + 1;
    }
    return str;
  }

  string down(string str, int location) {
    if (str[location] == '0') {
      str[location] = '9';
    } else {
      str[location] = str[location] - 1;
    }
    return str;
  }

    即 4 个转盘都可以转动一次。

  248. isInterleave

    还是暴力解，但我就是写不出来的。

    dp[i][j] 表示 s1[0..i] 和 s2[0..j] 能否构成 s3，然后 s[i], s[j] 都有可能符合，所以将它们都加进去，

        int res = 0;
    if (l1 < (int)s1.size() && s1[l1] == s3[l1 + l2]) {
      res = check(s1, l1 + 1, s2, l2, s3);
    }
    if (l2 < (int)s2.size() && s2[l2] == s3[l1 + l2]) {
      res = res || check(s1, l1, s2, l2 + 1, s3);
    }

    就是这点想不出来。

  249. sortedListToBST

    哈哈，终于会用递归了，找到中间节点，然后递归建立左右子树，

        if (!head) {
      return NULL;
    }
    if (!head->next) {
      return new TreeNode(head->val);
    }

    ListNode *one = head;
    ListNode *two = head;
    ListNode *pre;
    while (two && two->next) {
      pre = one;
      one = one->next;
      two = two->next;
      if (two) {
        two = two->next;
      }
    }

    ListNode *right = one->next;
    pre->next = NULL;
    TreeNode *root = new TreeNode(one->val);
    root->left = construct(head);
    root->right = construct(right);
    return root;

  250. searchInsert

    标准的二分查找，

        int left = 0;
    int right = (int)nums.size() - 1;
    int mid;

    while (left <= right) {
      mid = (left + right) / 2;
      if (nums[mid] > target) {
        right = mid - 1;
      } else if (nums[mid] < target) {
        left = mid + 1;
      } else {
        return mid;
      }
    }
    return target > nums[mid] ? mid + 1 : mid;

  251. trailingZeroes

    首先，两个数相乘结果末尾有 0，一定是因为两个数中有因子 2 和 5，也就是说，问题转化为：n! 最多可以分解出多少个因子 2 和 5？最多可以分解出多少个因子 2 和 5，主要取决于能分解出几个因子 5，因为每个偶数都能分解出因子 2，因子 2 肯定比因子 5 多得多。那么，问题转化为：n! 最多可以分解出多少个因子 5？难点在于像 25，50，125 这样的数，可以提供不止一个因子 5，不能漏数了。

    这样，我们假设 n = 125，来算一算 125! 的结果末尾有几个 0：

    首先，125 / 5 = 25，这一步就是计算有多少个像 5，15，20，25 这些 5 的倍数，它们一定可以提供一个因子 5。但是，这些足够吗？刚才说了，像 25，50，75 这些 25 的倍数，可以提供两个因子 5，那么我们再计算出 125! 中有 125 / 25 = 5 个 25 的倍数，它们每人可以额外再提供一个因子 5。够了吗？我们发现 125 = 5 x 5 x 5，像 125，250 这些 125 的倍数，可以提供 3 个因子 5，那么我们还得再计算出 125! 中有 125 / 125 = 1 个 125 的倍数，它还可以额外再提供一个因子 5。这下应该够了，125! 最多可以分解出 25 + 5 + 1 = 31 个因子 5，也就是说阶乘结果的末尾有 31 个 0。

  252. preimageSizeFZF

    对每个数用上一题的方法计算出其最后有几个 0，然后用二分法确定上下界。不过这种做法会超时。

    哦，原来不是算法有问题，是我的二分法写的有问题。以后按这个写，

      long upper(int k) {
    long left = 0, right = 2 * (long)INT_MAX;
    long mid;
    long num_zero;
    while (left < right) {
      mid = (left + right) / 2;
      num_zero = trailingZeroes(mid);
      if (num_zero > k) {
        right = mid;
      } else if (num_zero <= k) {
        left = mid + 1;
      }
    }
    return left - 1;
  }

  long lower(int k) {
    long left = 0, right = 2 * (long)INT_MAX;
    long mid;
    long num_zero;
    while (left < right) {
      mid = (left + right) / 2;
      num_zero = trailingZeroes(mid);
      if (num_zero >= k) {
        right = mid;
      } else if (num_zero < k) {
        left = mid + 1;
      }
    }
    return left;
  }

  253. moveZeroes

    这题只需要移动 0，所以使用 right 指针维护每一个非 0 的元素，用 left 维护去除 0 后的数组索引。

  254. removeElement

    和上题一样，用双指针。

  255. findKthLargest

    哈哈，直接 sort。

  256. nestedIterator

    没怎么看懂题目，就是一个多叉树的遍历。按照前序遍历将结果保存下来，然后逐个输出即可。

  257. myPow

    这题主要是注意临界情况不要越界。

  258. superPow

    计算 ab 对 1337 取模，a 是一个正整数，b 是一个非常大的正整数且会以数组形式给出。

    从后面开始遍历，这里会用到公式，

    • (a * b) % k = (a % k)(b % k) % k

    因为 “b 是一个非常大的正整数且会以数组形式给出”，所以每次需要计算 pow(a, 10)。

  259. isPossible

    解法真的巧妙。用一个 unordered_map<int, int> times 记录所有数字出现的次数，一个 unordered_map<int, int> order 记录所有以 k 结尾的字符串出现的次数。

    • 遍历所有的字符，如果该字符 i 出现的次数为 0，那么跳过这个字符；
    • 如果该字符 i 出现的次数不为 0，同时以 i - 1 结尾的字符串出现次数不为 0，那么该字符 i 就可以加入到字符串中，同时 order[i - 1]--; order[i]++；
    • 如果该字符 i 出现的次数不为 0，同时字符 i + 1, i + 2 出现次数不为 0，那么就可以构成一个新的字符串；
    • 如果上述条件都不满足，那么返回 false。

  260. diffWaysToCompute

    分治法，其实就是转换成二叉树然后递归计算子树，可以加上一个 unordered_map 来减少重复计算。

  261. examRoom

    用 set，这个容器可以按照元素大小插入。每次插入位置索引，然后计算两个元素间的距离，找到最大的插入。同时需要考虑在第一个位置插入，

    	int pos = 0, pre = -1, maxDist = 0;
    for (int cur : s) {
      int dist = (cur - pre) / 2;
      if (dist > maxDist) {
        pos = pre == -1 ? 0 : pre + dist; // .....5....这种情况就需要插入位置 0
        maxDist = pre == -1 ? cur : dist;
      }
      pre = cur;
    }

  262. isRectangleCover

    这题解法也很巧妙。首先遍历所有的点，计算位于 4 个角的点，同时计算所有矩形的面积和以及每个点出现的次数。如果理论上的矩形面积和计算出来的面积和不同，说明不是完美矩形；如果位于 4 个角的点不在所有给出来的点中，说明这些小矩形不能组成大的矩形；除了 4 个角的点，其他的点都只能出现 2 次或 4 次。

    最后使用 typedef pair<int, int> Point; 来表示一个点。

  263. minFallingPathSum

    不难，直接递归计算即可，但从后往前递归时间复杂度更好一点。

  264. numDistinct

    很难，这题好像从后面遍历，没做出来。

  265. calculateMinimumHP

    这题确实想不到。

    dp[i][j] 表示从 [i, j] 到终点需要的最小 HP，

    状态转移方程：

    int tmp = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j])，这个可以理解，到达下个最小 HP 需要的 HP，

    dp[i][j] = max(tmp, 1)，这个 1 是因为 HP 必须大于 1。

    dp base：

    到达终点的状态为 HP = 1，所以 dp[row][col -1] = dp[row - 1][col] =1。

  266. canCompleteCircuit

    我只能想出 O(n^2) 的暴力算法。

    首先计算 sum，如果 sum < 0 那么无解，而且解一定为最差情况（sum 最少的站点）的下一个站点。

  267. videoStitching

    先按照起点升序排序，如果起点相同的话按照终点降序排序，然后比较所有起点小于 end 的区间，根据贪心策略，它们中终点最大的那个区间就是下一个会被选中的区间，以此类推。

  268. PredictTheWinner

    这个是 stoneGame 的升级版，需要用动态规划来做，不能用取巧的方法。

    首先定义 dp[i][j][k] 的含义：

    • dp[i][j][0] 表示 piles[i ~ j] 石子堆中先手取能获得的最大值；

      dp[i][j][0] = max(piles[i] + dp[i+1][j][1], piles[j] + dp[i][j-1][1])
dp[i][j][0] = max(     选择最左边的石头堆     ,     选择最右边的石头堆      )
# 解释：我作为先手，面对 piles[i...j] 时，有两种选择：
# 要么我选择最左边的那一堆石头，然后面对 piles[i+1...j]
# 但是此时轮到对方，相当于我变成了后手；
# 要么我选择最右边的那一堆石头，然后面对 piles[i...j-1]
# 但是此时轮到对方，相当于我变成了后手。

if 先手选择左边:
    dp[i][j][1] = dp[i+1][j][0]
if 先手选择右边:
    dp[i][j][1] = dp[i][j-1][0]
# 解释：我作为后手，要等先手先选择，有两种情况：
# 如果先手选择了最左边那堆，给我剩下了 piles[i+1...j]
# 此时轮到我，我变成了先手；
# 如果先手选择了最右边那堆，给我剩下了 piles[i...j-1]
# 此时轮到我，我变成了先手。

    dp base：

    • dp[i][i][0] = piles[i]
    • dp[i][i][1] = 0

    最后计算 dp[0][n - 1][0] - dp[0][n - 1][1] 的差值。

  269. canIWin

    思路是对的，用 DFS 算法。任选一个数 i，如果这个数没有被使用过，那么可以使用这个数，如果 i >= desiredTotal 则直接返回 true；否则desiredTotal - i，让下一个人选，即递归调用 DFS，如果下一个人能赢，那么这个人就输了。

      bool dfs(int used, int total) {
    if (dp[used] == 0) {
      for (int i = 1; i <= maxChoosableInteger; i++) {
        if (used & (1 << i)) {
          continue;
        }
        if (total + i >= desiredTotal) {
          dp[used] = 1;
          return true;
        }
        // used |= (1 << i);
        // desiredTotal -= i;
        // if another one return true, it means this one is lose.
        if (!dfs(used | (1 << i), total + i)) {
          dp[used] = 1;
          return true;
        }
        // desiredTotal += i;
        // used &= (0 << i);
      }
      dp[used] = false;
    }
    return dp[used];
  }

  270. getMoneyAmount

    看题目给的图我首先想到的是二分法，但是二分法是错误的，应该直接用 DFS 计算所有的数，然后取这个数左右两侧的最大值，再取所有数中的最小值。

  271. findClosestElements

    这道题比较简单，直接双指针即可。

  272. maxCoins

    DFS 是正确的，但是复杂度太高了。

        // if (!map[nums]) {
    int n = nums.size();
    if (n == 1) {
      return nums[0];
    }

    int res = 0, tmp;
    vector<int> tmpnums;
    for (int i = 0; i < n; i++) {
      if (i - 1 == -1) {
        tmp = nums[i] * nums[i + 1];
      } else if (i + 1 == n) {
        tmp = nums[i - 1] * nums[i];
      } else {
        tmp = nums[i - 1] * nums[i] * nums[i + 1];
      }

      tmpnums.assign(nums.begin(), nums.end());
      tmpnums.erase(tmpnums.begin() + i);
      res = max(res, dfs(tmpnums) + tmp);
    }
    return res;
    // map[nums] = res;
    // }
    // return map[nums];

  273. findRotateSteps

    好吧，暴力贪心是错误的。

    还是用 DFS，这个好好用，暴力遍历必选啊！不过想不到子问题是什么。这题的子问题是因为 ring 中可能有多个同样的字符，所以这些字符都要遍历，选择这些字符中结果最小的，然后用一个额外的数组进行枝减。

      int dfs(string ring, int m, string key, int n) {
    if (n == (int)key.size()) {
      return 0;
    }
    if (dp[m][n]) {
      return dp[m][n];
    }

    int length = ring.size();
    int res = INT_MAX;
    for (auto k : map[key[n]]) {
      int dis = abs(m - k);
      dis = min(dis, length - dis);
      int tmp = dfs(ring, k, key, n + 1);
      res = min(res, 1 + tmp + dis);
    }
    dp[m][n] = res;
    return dp[m][n];
  }

  274. numEnclaves

    简单的 DFS。

  275. closedIsland

    还是 DFS，将边缘的 '0' 及其相连的 ‘0’ 转换为 ‘1’，那么剩下的就都是岛屿。遍历所有的格点，遇到岛屿计数器就加 1，同时将 ‘0’ 转换为 ‘1’，这样就能计算出所有的岛屿。

  276. isValidSudoku

    简单。

  277. simplifyPath

    这题还是用栈才能做的出来。

    从前往后处理 path，每次以 item 为单位进行处理（有效的文件名），根据 item 为何值进行分情况讨论：

    item 为有效值 ：存入栈中； item 为 .. ：弹出栈顶元素（若存在）； item 为 . ：不作处理。

  278. partitionLabels

    这题使用贪心，计算每个字符最后出现的位置，然后进行划分。

  279. largestNumber

    这题我还想复杂的比较函数呢，直接这样就可以了，

    static bool cmp(string s1, string s2) { return s1 + s2 > s2 + s1; }

  280. findLongestWord

    只能想出 0(n^3) 的算法。

  281. removeKdigits

    这题用单调栈做。

  282. partition

    这题虽然之前做过类似的，但还是想不出来。判断每个字符是否是回文字符，如果是的话检查下一个子串；如果不是则继续增加子串的长度。

  283. countSubIslands

    这题开始想遇到 grid1[i][j] != 1 就返回 false，但是写出来，所以维护一个全局变量。

  284. MagicDictionary

    这题直接用暴力匹配比较简单，反倒是用 trie 树很难调。

  285. updateMatrix

    这题很有意思，虽然用的还是 BFS，但是引入多源的概念，将所有的 0 都如栈，然后计算距离。

  286. findLength

    这是一道典型的动态规划，但是我居然没有想出来。但是动态转移方程又有些不一样，扩展一种思路。

  287. arrayNesting

    是的，用图的方法更简单，但面试的时候不一定能想出来。因为数组不包含重复元素，所以将数组连成图的话肯定会构成一个或多个环，找到最大的那个即可。

  288. combinationSum_iv

    这题做过类似的，但想不到它类似与爬楼梯那题，其实回溯也可以做，只是超时了，然后这题和 coinchange 也类似，但是那题无法计算重复的情况，如 [1,1,2] 和 [1,2,1]。

  289. minSteps

    确实，这题用 dfs 很正常。

  290. maxScoreSightseeingPair

    这种给出公式的数学题要尝试从公式入手。将其拆分成 values[i]+i 和 values[j]−j 两部分，这样对于统计景点 j 答案的时候，由于 values[j]−j 是固定不变的，因此其实就等价于求 [0,j-1] 中 values[i]+i 的最大值 mx，景点 j 的答案即为 mx+values[j]−j。而 mx 的值我们只要从前往后遍历 j 的时候同时维护即可。

  291. sequenceReconstruction

    原来这题用的是拓扑排序，而拓扑排序的关键就是不断找到图中入度为 0 的节点入对，然后用 bfs 遍历与该节点相连的点，计算其入度是否为 0。

reference

[1] https://github.com/labuladong/fucking-algorithm/blob/master/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%B3%BB%E5%88%97/%E9%AB%98%E6%A5%BC%E6%89%94%E9%B8%A1%E8%9B%8B%E8%BF%9B%E9%98%B6.md

[https://leetcode.cn/problems/fan-zhuan-lian-biao-lcof/]:

About

No description, website, or topics provided.

Resources

Readme
Activity

Stars

0 stars

Watchers

1 watching

Forks

0 forks
Report repository

Releases

No releases published

Packages

No packages published

Languages