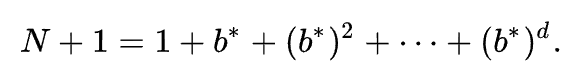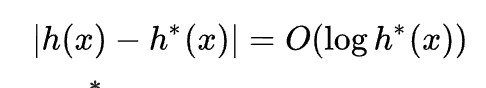Table of Contents
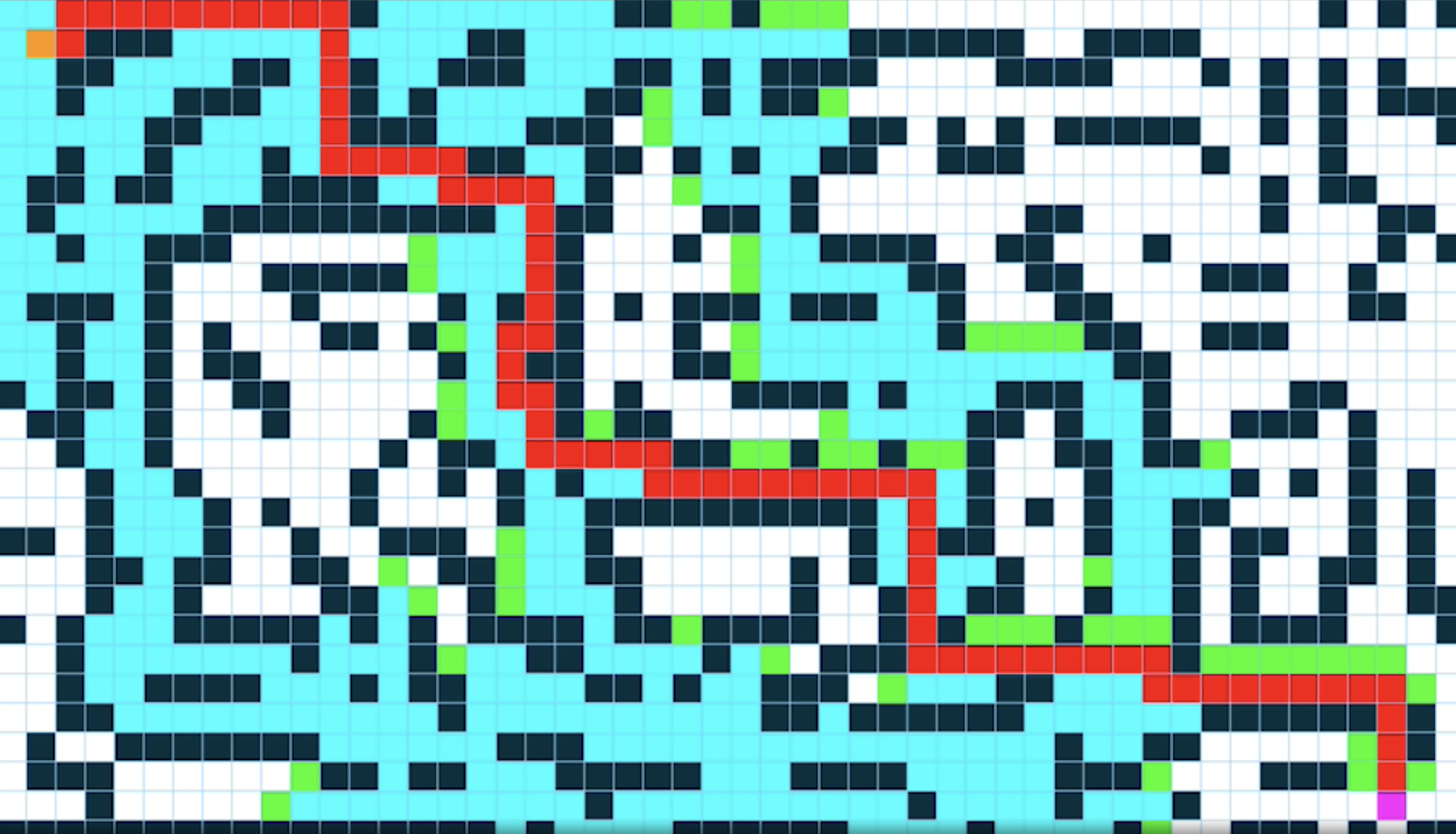
This project focuses on the use of search algorithms (A*) applied to heuristic and informed graphs. The goal of this is to find the shortest path between two points, where the start marker is orange and the end marker is purple.
A* (pronounced "A-star") is a graph traversal and path search algorithm, which is often used in many fields of computer science due to its completeness, optimality, and optimal efficiency.One major practical drawback is its O(b^d) space complexity, as it stores all generated nodes in memory. Thus, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance,as well as memory-bounded approaches; however, A* is still the best solution in many cases.
The time complexity of A* depends on the heuristic. In the worst case of an unbounded search space, the number of nodes expanded is exponential in the depth of the solution (the shortest path) d: O(bd), where b is the branching factor (the average number of successors per state).This assumes that a goal state exists at all, and is reachable from the start state; if it is not, and the state space is infinite, the algorithm will not terminate.
The heuristic function has a major effect on the practical performance of A* search, since a good heuristic allows A* to prune away many of the bd nodes that an uninformed search would expand. Its quality can be expressed in terms of the effective branching factor b*, which can be determined empirically for a problem instance by measuring the number of nodes generated by expansion, N, and the depth of the solution, then solving:
Good heuristics are those with low effective branching factor (the optimal being b* = 1).
The time complexity is polynomial when the search space is a tree, there is a single goal state, and the heuristic function h meets the following condition:
where h* is the optimal heuristic, the exact cost to get from x to the goal. In other words, the error of h will not grow faster than the logarithm of the "perfect heuristic" h* that returns the true distance from x to the goal.
The space complexity of A* is roughly the same as that of all other graph search algorithms, as it keeps all generated nodes in memory. In practice, this turns out to be the biggest drawback of A* search, leading to the development of memory-bounded heuristic searches, such as Iterative deepening A*, memory bounded A*, and SMA*.
What sets A* apart from a greedy best-first search algorithm is that it takes the cost/distance already traveled, g(n), into account.
Some common variants of Dijkstra's algorithm can be viewed as a special case of A* where the heuristic h(n) = 0 for all nodes;in turn, both Dijkstra and A* are special cases of dynamic programming.A* itself is a special case of a generalization of branch and bound.
-
Clone the repo
git clone https://github.com/abaron10/Pathfinding_visualizer.git
-
Create virtual environment
virtualenv vnv
- Activate virtualenv
source vnv/bin/activate
- On root, run the project
python3 Visualizer.py
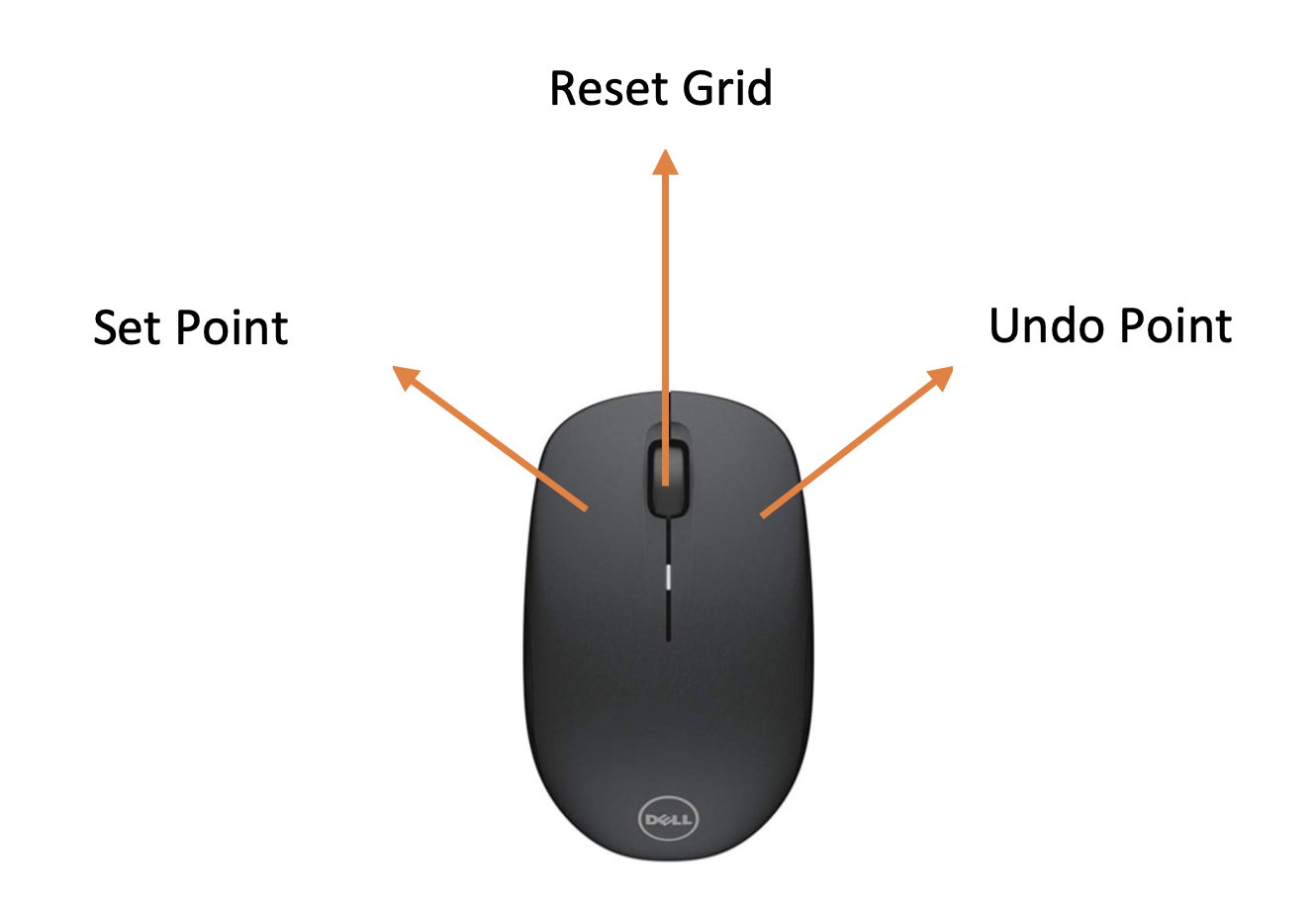
| Button | Task |
|---|---|
| Left Click | Create / Set a new start-end-barrier node |
| Middle Click | Reset Grid |
| Right Click | Undo start-end-barrier node |
Contributions are what make the open source community such an amazing place to be learn, inspire, and create. Any contributions you make are greatly appreciated.
- Fork the Project
- Create your Feature Branch
- Commit your Changes
- Push to the Branch
- Open a Pull Request
Distributed under the MIT License. See LICENSE for more information.
https://www.linkedin.com/in/andres-baron-sandoval-76ab96186/ - af.baron10@uniandes.edu.co
Project Link: https://github.com/abaron10/Pathfinding_visualizer