This project aims to make arrays of sizes 10,..., and 1M, consisting of random values using a random number generator. Then sort, using different sorting algorithms and get the compiler time, compare it with their theoretical runtime.
The main part of this project was to get the compiler time of the sorting algorithms. Initially, I wrote my code on VS Code editor on windows and the compiler I used was MinGW. The driver code of each program is similar, and array size was taken as input. First, I run the programs using a test array to make sure that the program is working currently. I was getting different times with the same size array for every algorithm. The variation was not minor sometimes I was getting almost double to time, but after a couple of runs, I started to get similar results. I did change the clock function to make sure it’s not the clock. The result was the same then I decided to take an average time of 5 runs. Everything worked fine but whenever I enter an array size of 1M my program would crash. I thought there might be a limit to the random generator but turns out it wasn’t the problem. I tried to use an online compiler which worked but the variations were significant sometimes. The problem was solved after changing the operating system. I did not have Linux previously so, I had to set up Linux on Virtual Box. Everything worked perfectly. The variation in time was also minor.
The implementation of the algorithms was not as bad as I expected. I had no problem implementing the insertion sort algorithm. It was simple and easy to follow. For merge sort, I had some trouble, first few tries implementing the pseudo-code I did not get the correct result, I decided to use the while loop instead of for loop, which worked, and I made the changes accordingly. I did not face many problems with the heapsort and quicksort either, it was easy to implement using the pseudo-code from the book. For the radix sort, I had to do the same research to implement the pseudocode. My code ended a little differently than the pseudocode, but it works as expected.
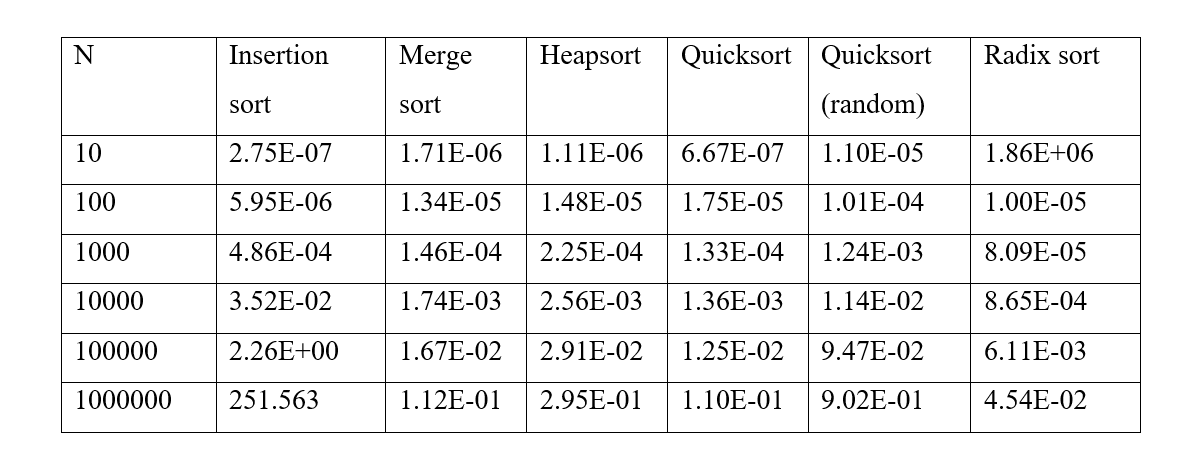
As for time complexity, insertion sort was vastly different than other sorting algorithms, although it took less time to sort array sizes up to 1k but after that difference was multiple orders of magnitude. First few runs I had to quit the program because it was taking so long, and I thought my system froze. As with other algorithms, the difference was not that different, as we can see in the graphs below. They follow the same trend as the theoretical time complexity. radix sort being the fastest. Time for Quicksort Random was unique. Each run time differs with higher variation than other algorithms. This is expected as each run the pivot was randomized so depending on the location of the pivot time differs.