An Evolutionary Algorithm for Solving the Two-Dimensional Packing Problem Combined with the 0/1 Knapsack Problem

Introduction

This project contains the code to solve a combination of the Packing Problem and the Knapsack Problem in 2D: different items with value, weight and shape can be placed in a container (of a certain shape), and the goal is to maximize the value of items placed in the container, without geometric intersections nor exceeding a maximum weight limit (capacity) of the container. Check the report for a more detailed explanation of the problem, the developed algorithms (present in the "KnapsackPacking") and the performed experiments (whose results, including many plots, can be found in the "Output" folder).

Performing experiments

To run the code, Python 3.x is required, with the following packages:

• matplotlib
• numpy
• pandas
• pickle
• shapely

The file to run is "problem_experiments.py". An IDE is recommended, but running from terminal should be possible too. By default, the problems created in functions invoked by "create_problems()" are used, but you can replace them with your own problem definitions, following the same syntax scheme.

This repository includes files that summarize experiments. You can set whether the saved experiments should be loaded (or otherwise run new ones) in the following line:

load_experiments = True

You can set how many times to run each algorithm on each problem, and whether multiple process (how many) should be used:

execution_num = 10
process_num = 10

When performing experiments, you can select which data should be saved or plotted:

show_problem_stats = False
save_problem_stats = False
show_manual_solution_plots = False
save_manual_solution_plots = False
show_algorithm_solution_plots = False
save_algorithm_solution_plots = False
show_value_evolution_plots = False
save_value_evolution_plots = False
show_time_division_plots = False
save_time_division_plots = False
show_algorithm_comparison = False
save_algorithm_comparison = False
show_aggregated_result_tables = True
save_aggregated_result_tables = False

You can change the implementation or default parameters of the developed algorithms in their respective files:

• Evolutionary algorithm in "evolutionary.py".
• Greedy algorithm in "greedy.py".
• Reversible algorithm in "reversible.py"

The supported shapes for items are:

• Polygons (supported by Shapely).
• Compound polygons with holes, a.k.a. multi-polygons (supported by Shapely).
• Circles (added in "circle.py").
• Ellipses (added in "ellipse.py").

You can add new shapes if you want, by first checking how circles and ellipses were defined (and their intersection checks with the rest of items).

Solution examples

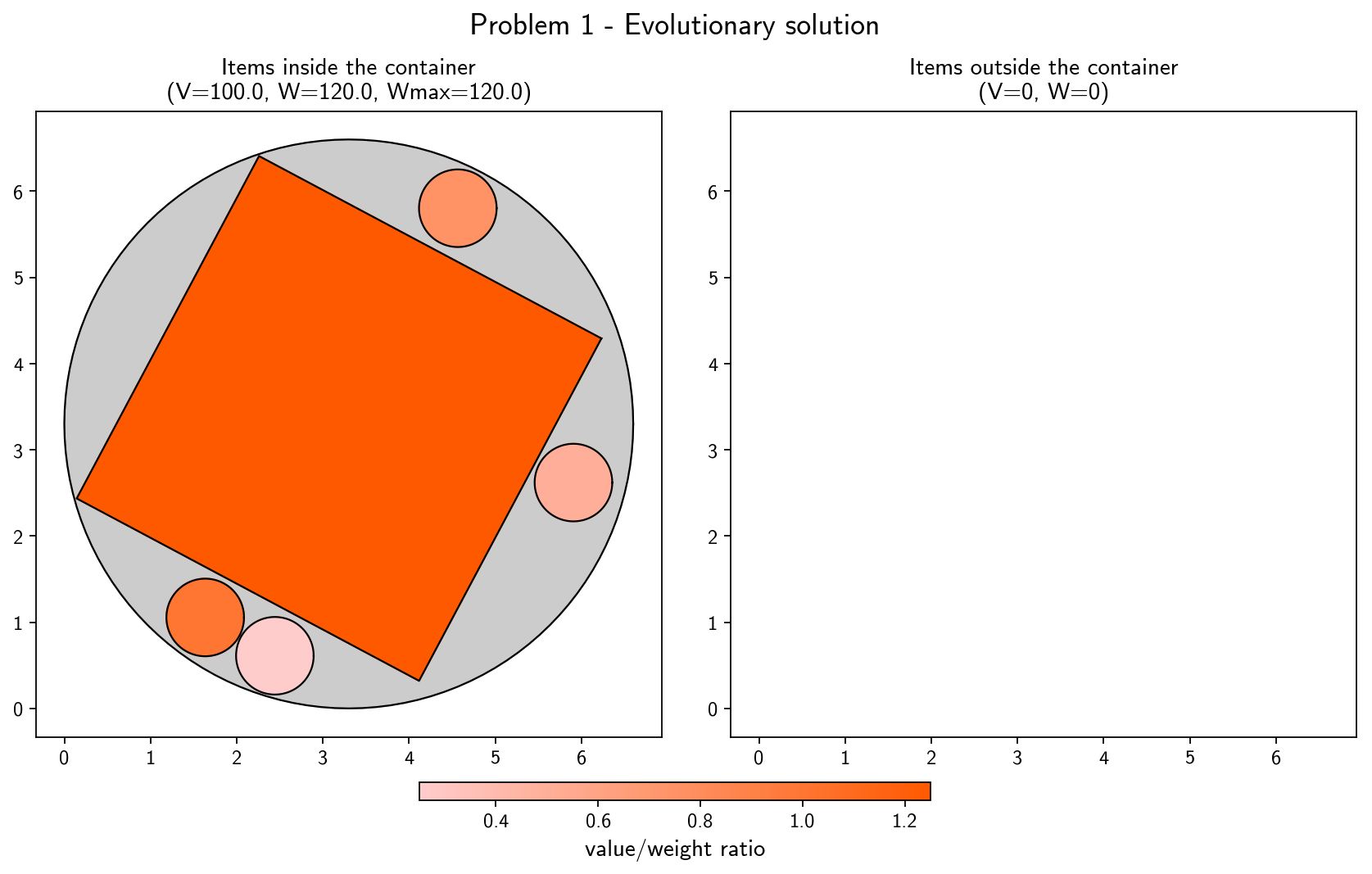
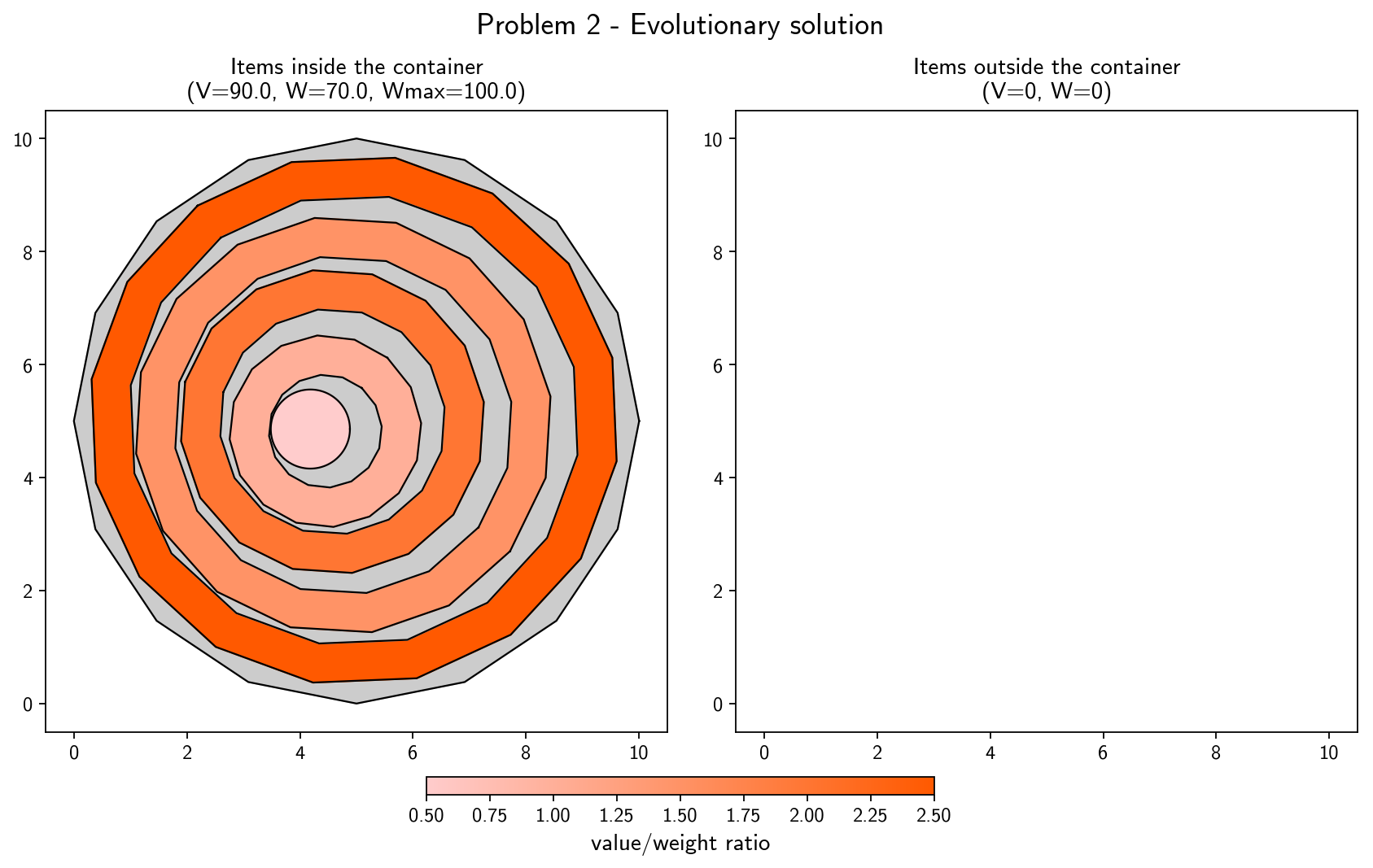
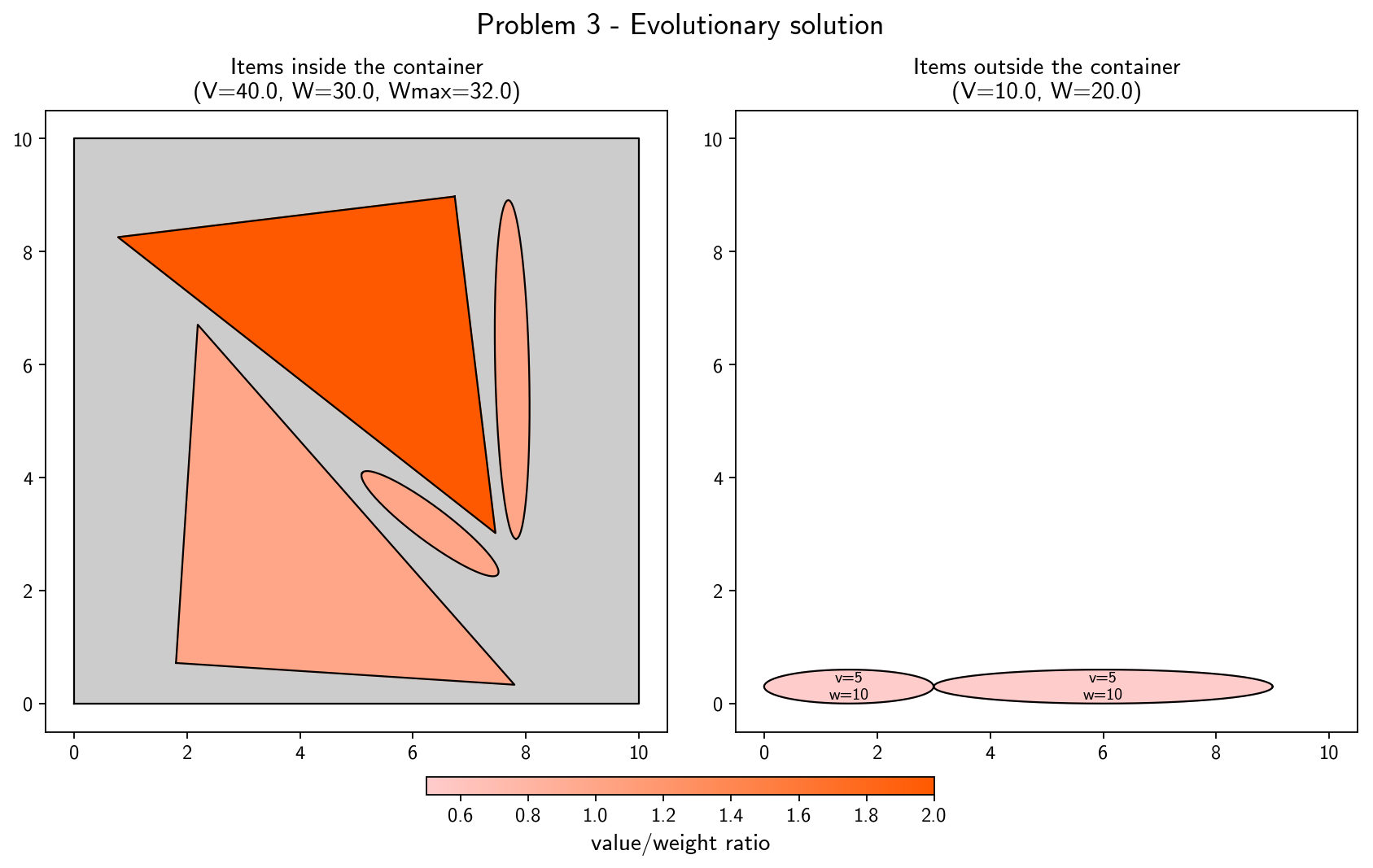
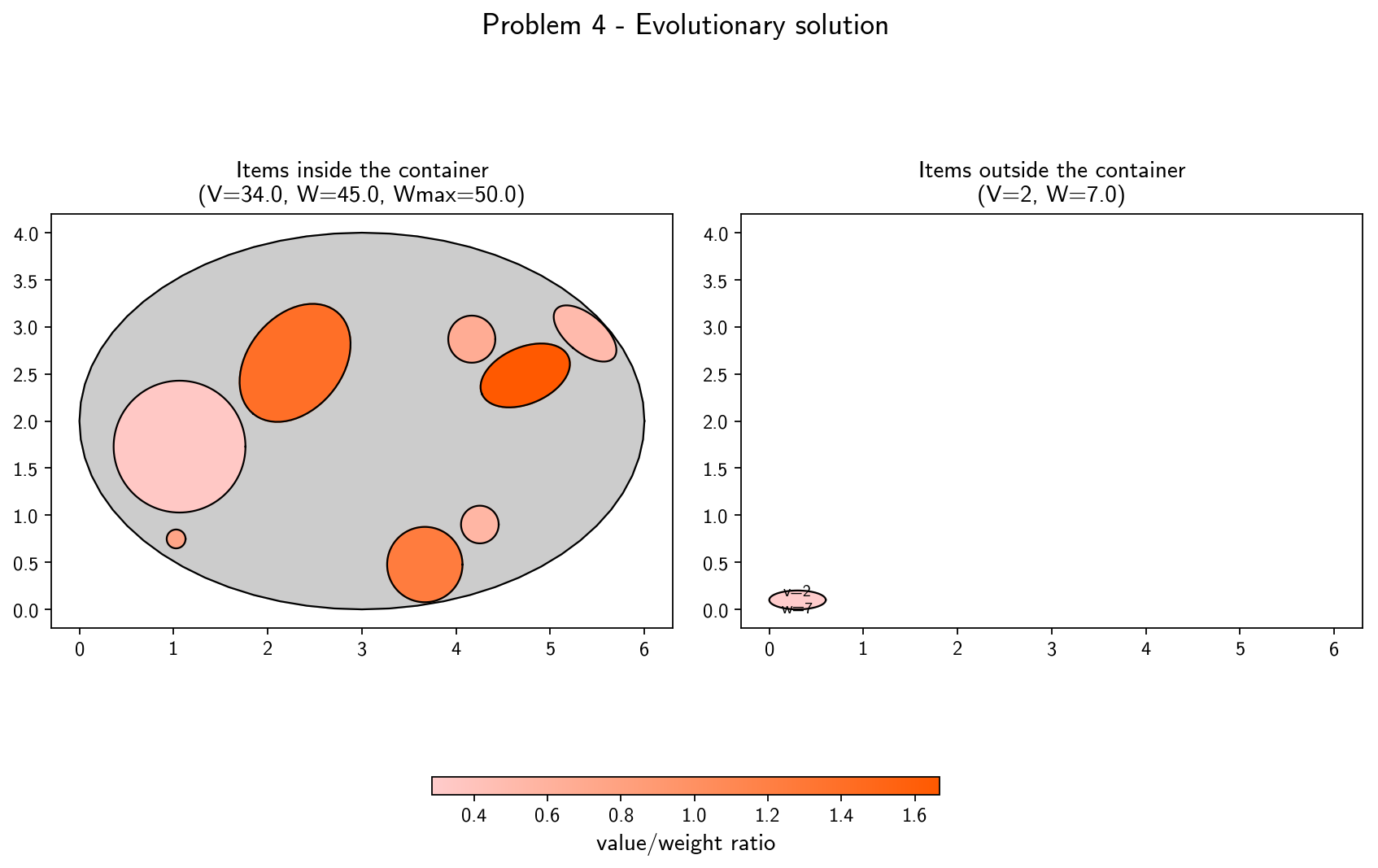
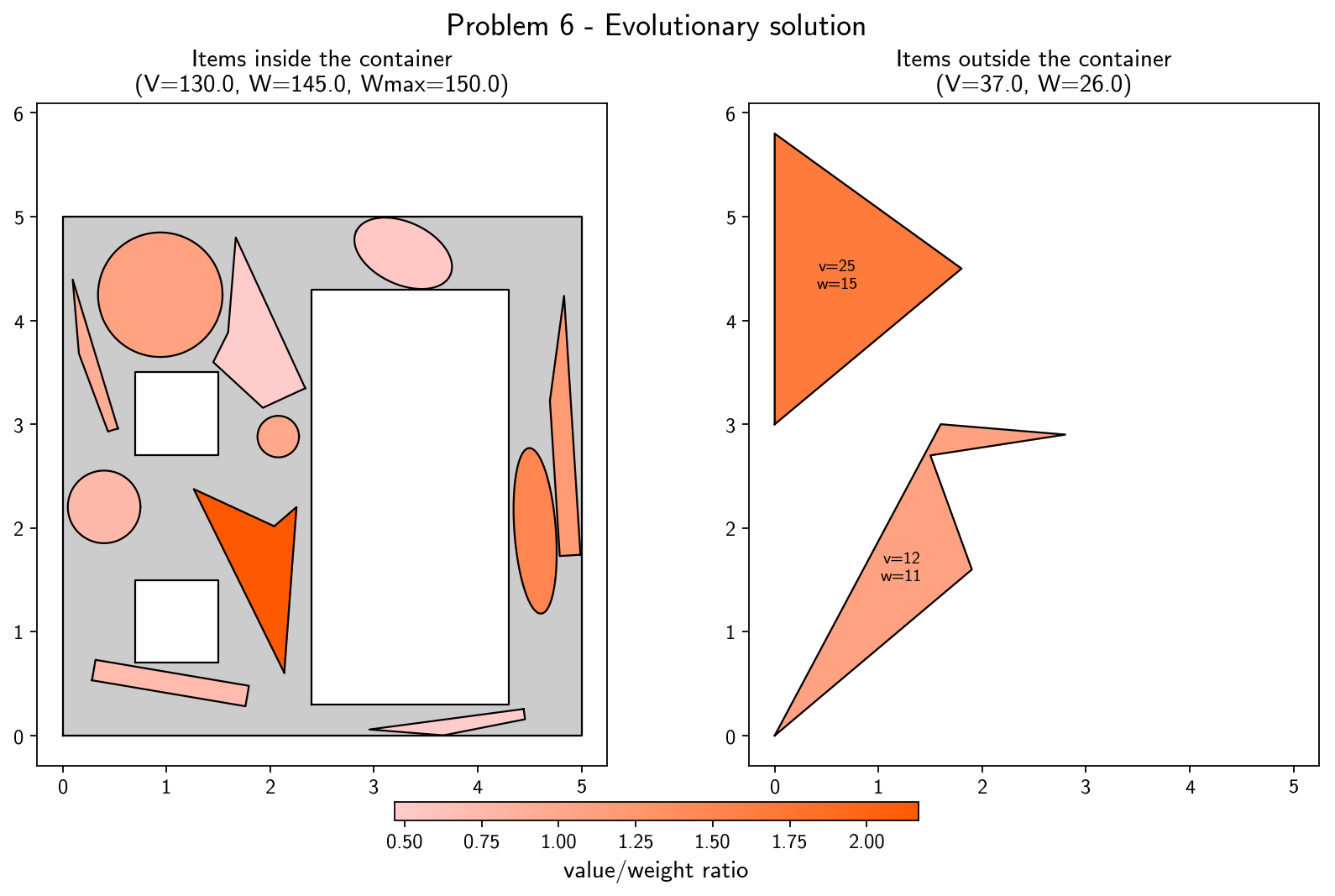
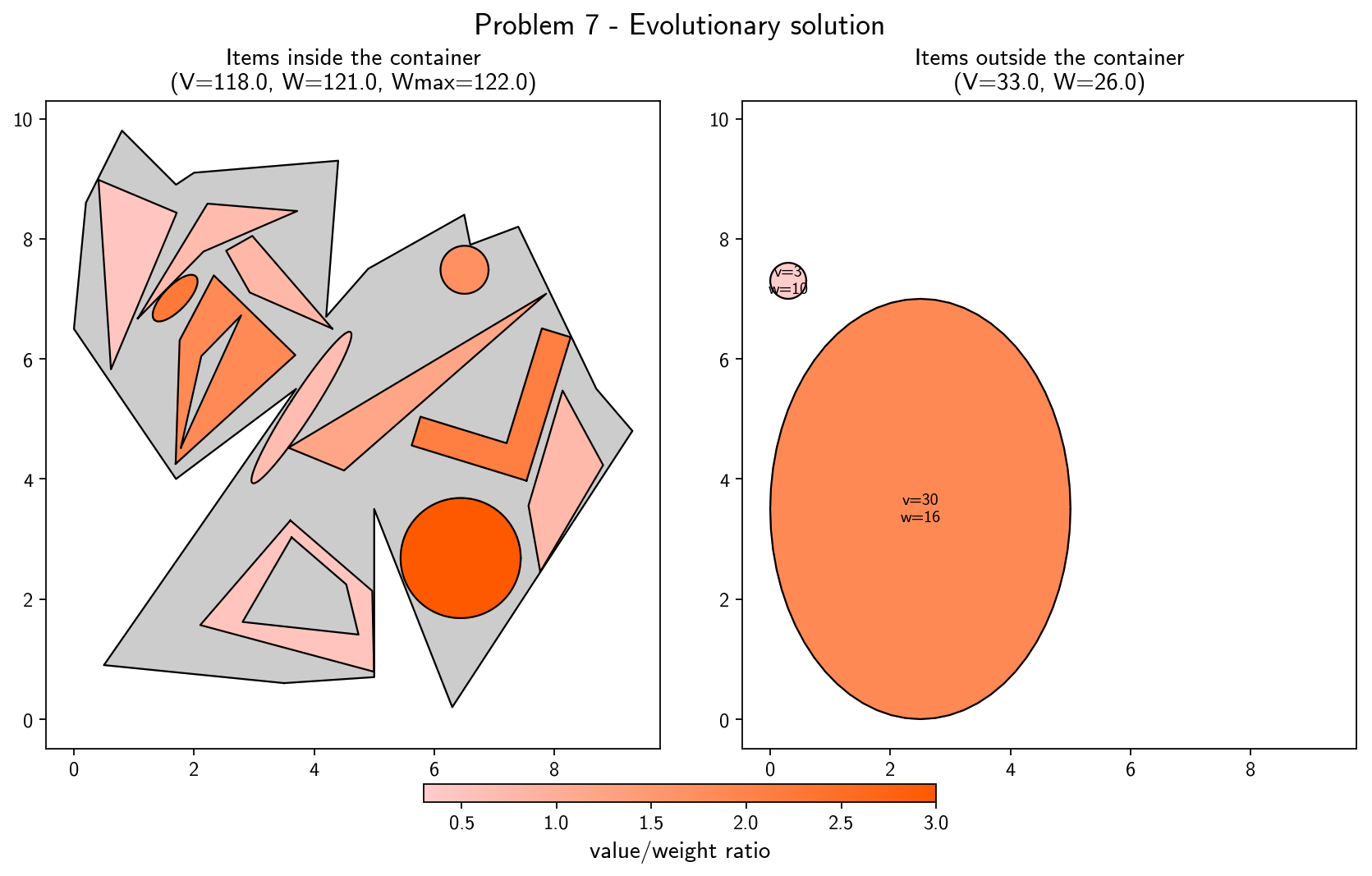
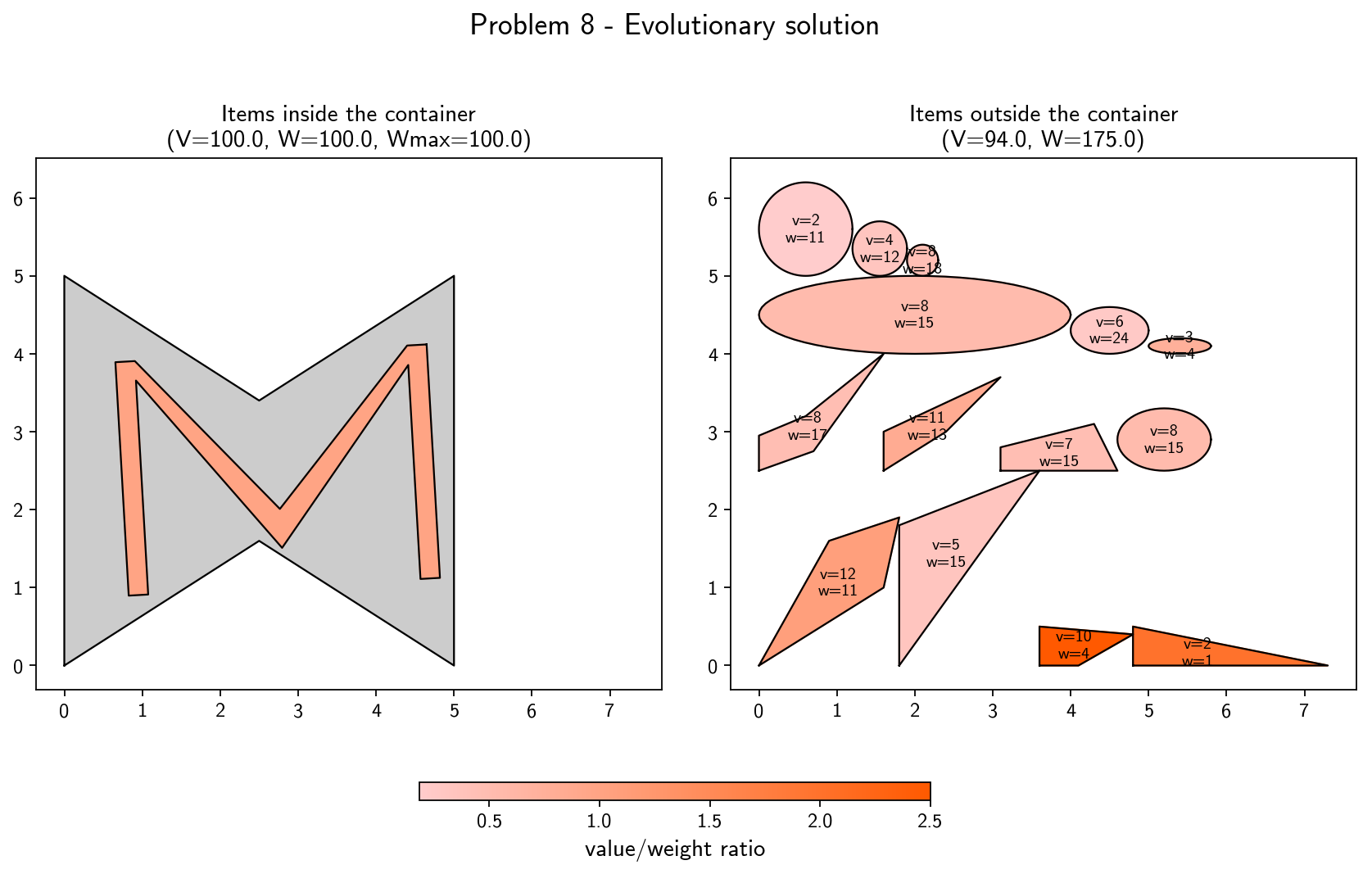
The solutions obtained by the evolutionary algorithm for some of the tested problems are shown below. In these 7 problems, the result is optimal, i.e. the maximum possible value is obtained. In the Joint (Knapsack + Packing) Problem, a solution can be optimal even if some items are left outside of the container (even if there is enough geometrical space available), namely in cases where the weight limit would be exceeded and no other combination of placed items would have yielded higher value. More details about these and other problems can be found in the report.

Research context

This work was submitted as Master Thesis for Master in Artificial Intelligence of Universitat Politècnica de Catalunya (UPC), in January 2020. The official publication in the repository of the University can be found here.