Density Functional Theory in real space, for atoms, both LDA and LSDA
Description is on the Computational Physics Blog: https://compphys.go.ro/dft-for-an-atom/
I changed the code to 'shoot' from both 'infinity' and from the nucleus and meet and match the solutions. Still does not work very well for heavy atoms, but for the program purpose it seems to work okish.
As it's LDA (originally that was the case, now it has LSDA as well) and there is the assumption of spherical symmetry (for non occupied shells you don't really have it except for the 'special' cases when you go with LSDA, for the others there is cylindrical symmetry), it kind of works only for noble gases, but you can get quite ok results for other atoms, too.
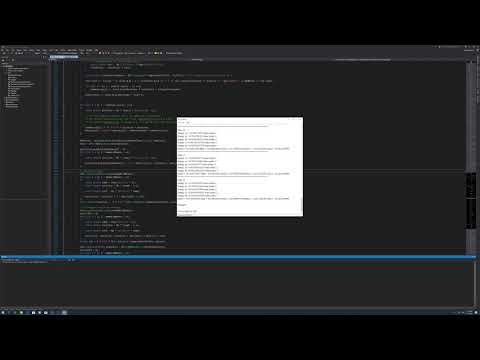
Here is what I get in a bad scenario, Radon:
Step: 53
Energy 1s: -3204.756288 Num nodes: 0
Energy 2s: -546.577961 Num nodes: 1
Energy 2p: -527.533025 Num nodes: 0
Energy 3s: -133.369145 Num nodes: 2
Energy 3p: -124.172863 Num nodes: 1
Energy 3d: -106.945007 Num nodes: 0
Energy 4s: -31.230804 Num nodes: 3
Energy 4p: -27.108985 Num nodes: 2
Energy 4d: -19.449995 Num nodes: 1
Energy 4f: -8.953318 Num nodes: 0
Energy 5s: -5.889683 Num nodes: 4
Energy 5p: -4.408703 Num nodes: 3
Energy 5d: -1.911330 Num nodes: 2
Energy 6s: -0.626571 Num nodes: 5
Energy 6p: -0.293180 Num nodes: 4
Etotal = -21861.346900 Ekin = 21854.672704 Ecoul = 8632.016044 Eenuc = -51966.120394 Exc = -381.915254
Finished!
1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 4f14 5s2 5p6 5d10 6s2 6p6
I used LSD, 17 for 'multigrid levels' (that means 131073 nodes) 0.0001 for delta, mixing 0.5 and the max radius 50. The results are not perfect, I guess with some other parameters they might be improved somewhat. The energy levels usually get all decimals given by NIST right, but occasionally the last one is wrong. The problem is for total energies, the total energy gets three decimals right, the partial ones get four or five decimals right. Here are the NIST values for comparison: https://www.nist.gov/pml/atomic-reference-data-electronic-structure-calculations/atomic-reference-data-electronic-7-70 Using LSDA I've got basically the same results. The last digit from total energies was ocassionaly different, but the total energy was the same. Exc was the same.
For a lighter noble gas I get better results, for Argon for example:
Step: 32
Energy 1s: -113.800134 Num nodes: 0
Energy 2s: -10.794172 Num nodes: 1
Energy 2p: -8.443439 Num nodes: 0
Energy 3s: -0.883384 Num nodes: 2
Energy 3p: -0.382330 Num nodes: 1
Etotal = -525.946200 Ekin = 524.969813 Ecoul = 231.458124 Eenuc = -1253.131983 Exc = -29.242154
Finished!
1s2 2s2 2p6 3s2 3p6
I used 14 for 'multigrid levels' (that means 16385 nodes), 0.0005 for delta, mixing 0.5 and the max radius 25. The energy levels results match all given decimals from NIST. The total energy gets three decimals right, the kinetic, coulomb energy six, nuclear energy five, the exchange correlation one seems to be the worse, with only four decimals (maybe there is room for improvement there?).
Here is the NIST data for comparison: https://www.nist.gov/pml/atomic-reference-data-electronic-structure-calculations/atomic-reference-data-electronic-7-16
There are slight differences in totals compared with the previous values I put here, possibly because I changed the integration to Romberg.
The program is faster than I expected, especially because I went to multi-grid instead of Numerov (or Runge-Kutta) for Poisson, so I expected it to be slower than with the other approach.