My OpenGL Projects

This repository contains a few of the OpenGL projects I've worked on. It starts with basic 2-d projects, such as the Sierpinski triangle, or building a convex hull around points using Graham's scan algorithm, all the way up to implementing elastic sphere collisions in 3-d space. All my projects make use of only GLUT. You won't need any other external libraries such as GLM, everything required is implemented from scratch.

To start working with GLUT on Windows using Visual Studio, follow this tutorial on GeeksforGeeks.

2-d projects

Sierpinski Triangle

The Sierpinski Triangle is a triangular fractal that can be formed algorithmically. Here, I'm using the chaos game approach to generate it:

1. A point is chosen (at random) within a triangular region (bounded by 3 vertices).
2. One of the 3 vertices is randomly chosen.
3. The midpoint of the randomly chosen point and vertex is plotted.
4. The plotted point is used as the randomly chosen point from step 1, and the consequent steps are repeated for several iterations.

I ran the algorithm for 50,000 iterations, and this is how the output looks:

Convex Hull Using Graham's Scan

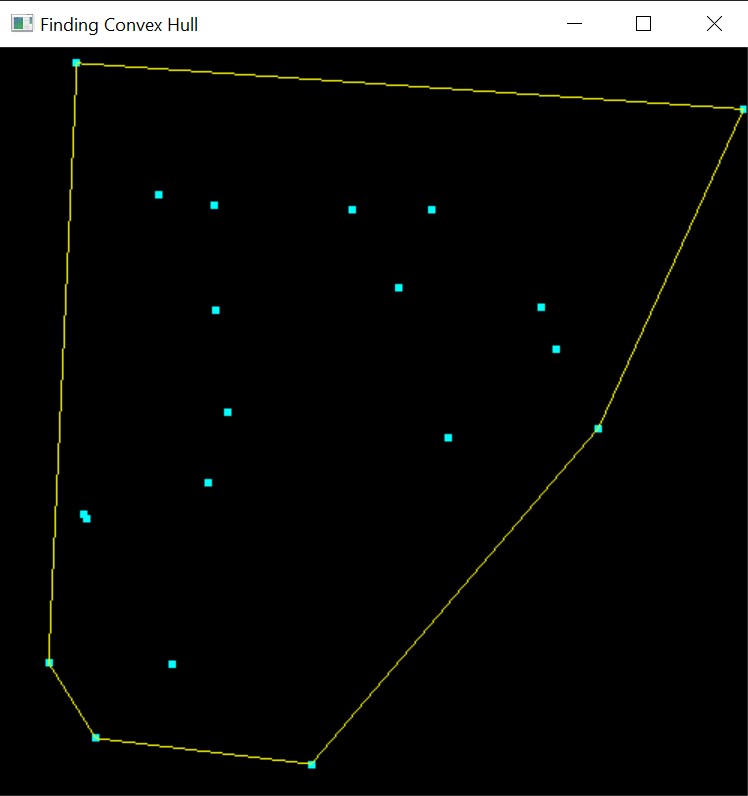
The Graham's scan is a way of finding the convex hull of a set of coplanar points in O(n log(n)) time. We start by having a collection of points. In my case, I created a function to randomly plot n points.

1. Select the left-most point out of the set of points.
2. Sort all the remaining points by the angle subtended at the left-most point.
3. Now start at the left most point and go in order of the remaining points. We know that on the convex hull, we should have only left turns as we move through the points. So we keep pushing points into the stack as we move through them, but if a particular point causes us to take a right turn with the next point, then we pop it from the stack.
4. Finally, we join the last point to the initial point and we have ourselves a convex hull.

This is how the output looks for 20 randomly generated points:

3-d Projects

Camera Controls

In all of these projects, the camera position can be adjusted using the following keys:
W - to move the camera forwards.
S - to move the camera backwards.
A - to move the camera clockwise around subject.
D - to move the camera counterclockwise around subject.
I - to move the camera up.
K - to move the camera down.

Sphere

Triangles are the most fundamental 2-d geometric object, and can be used to build virtually any 3-d object. In this project, I used triangles to build a sphere.

This is how the sphere looks:

Here's how the sphere looks from the inside:

Sphere Collisions

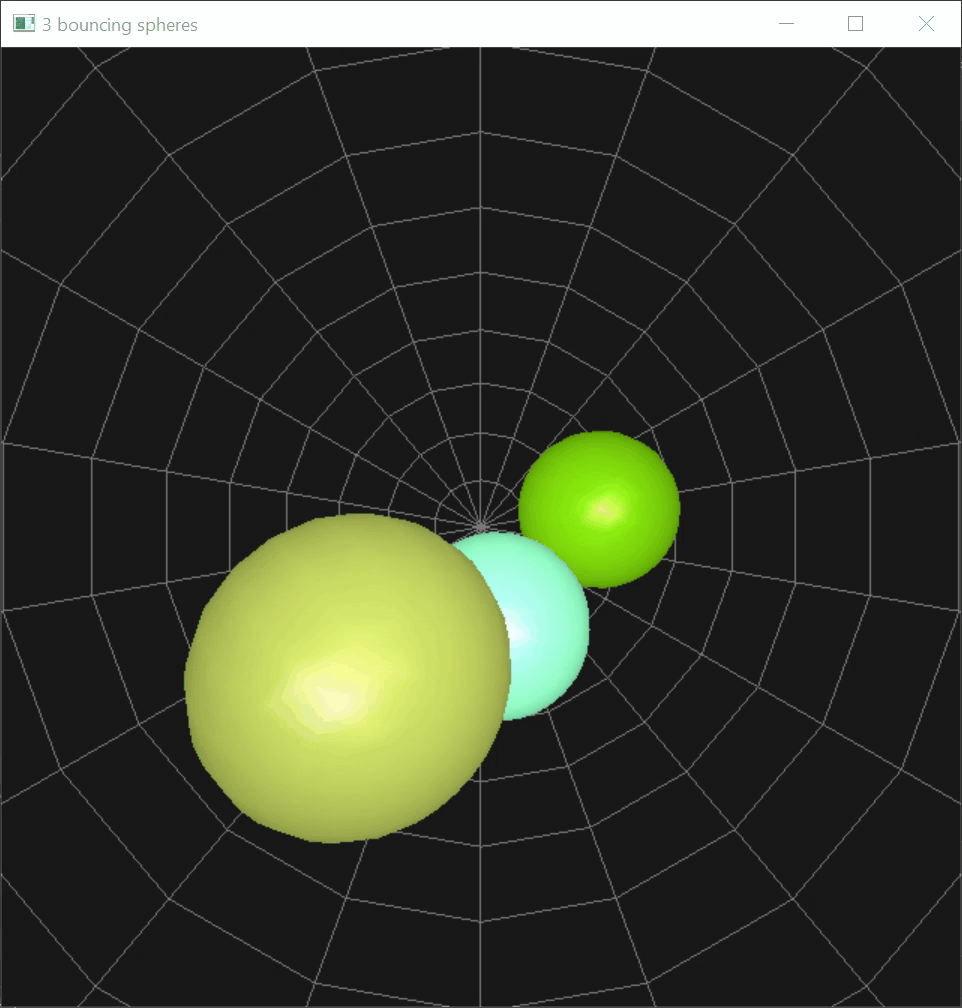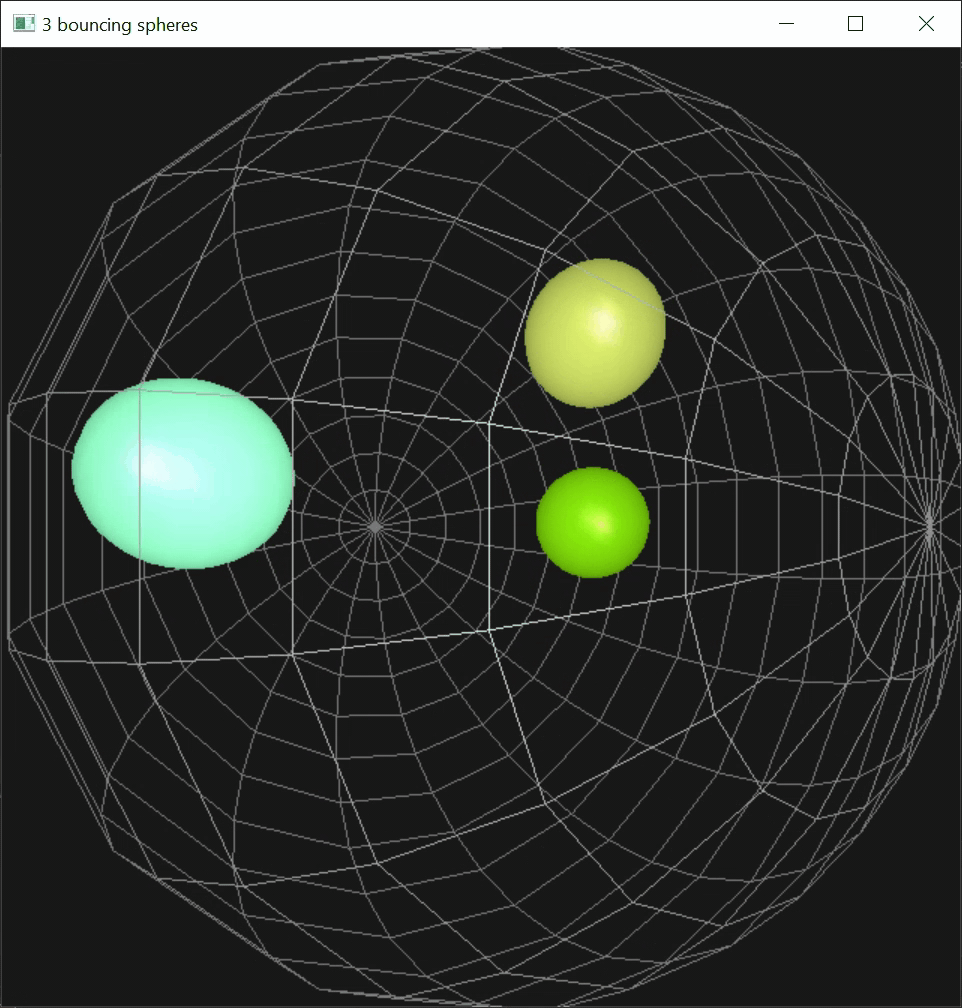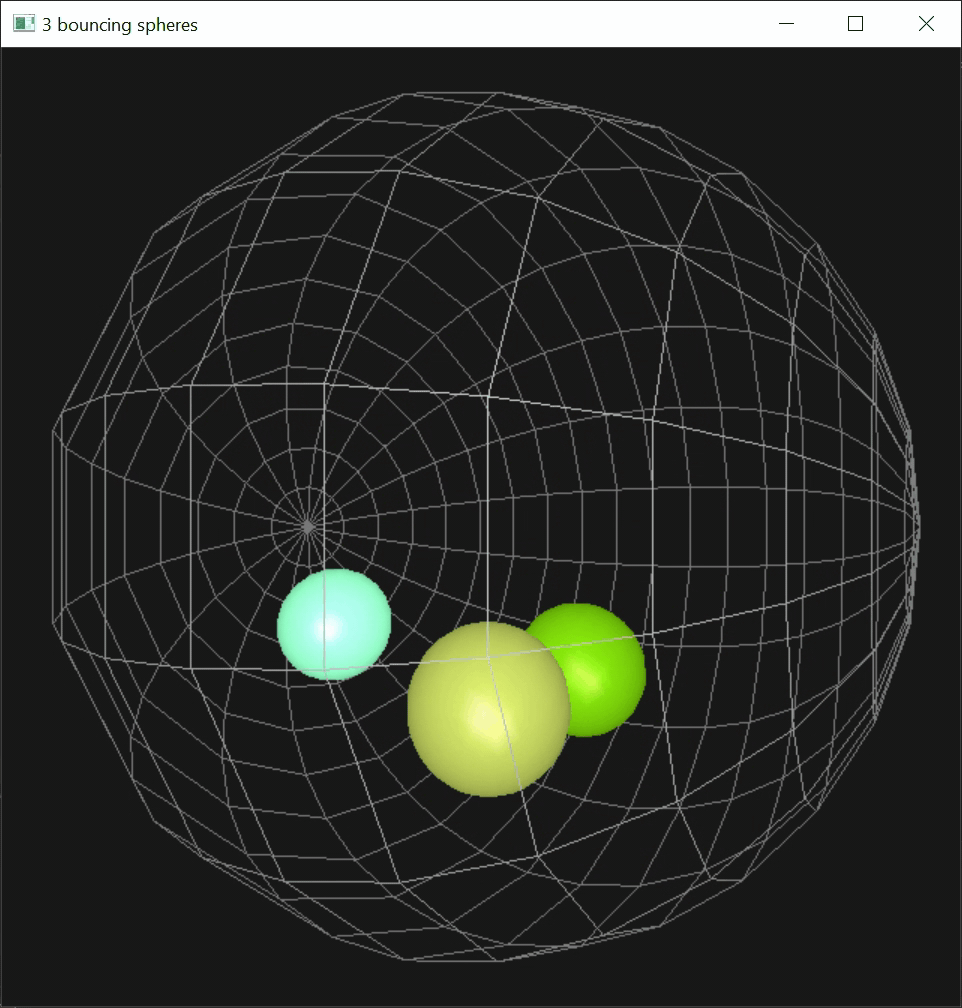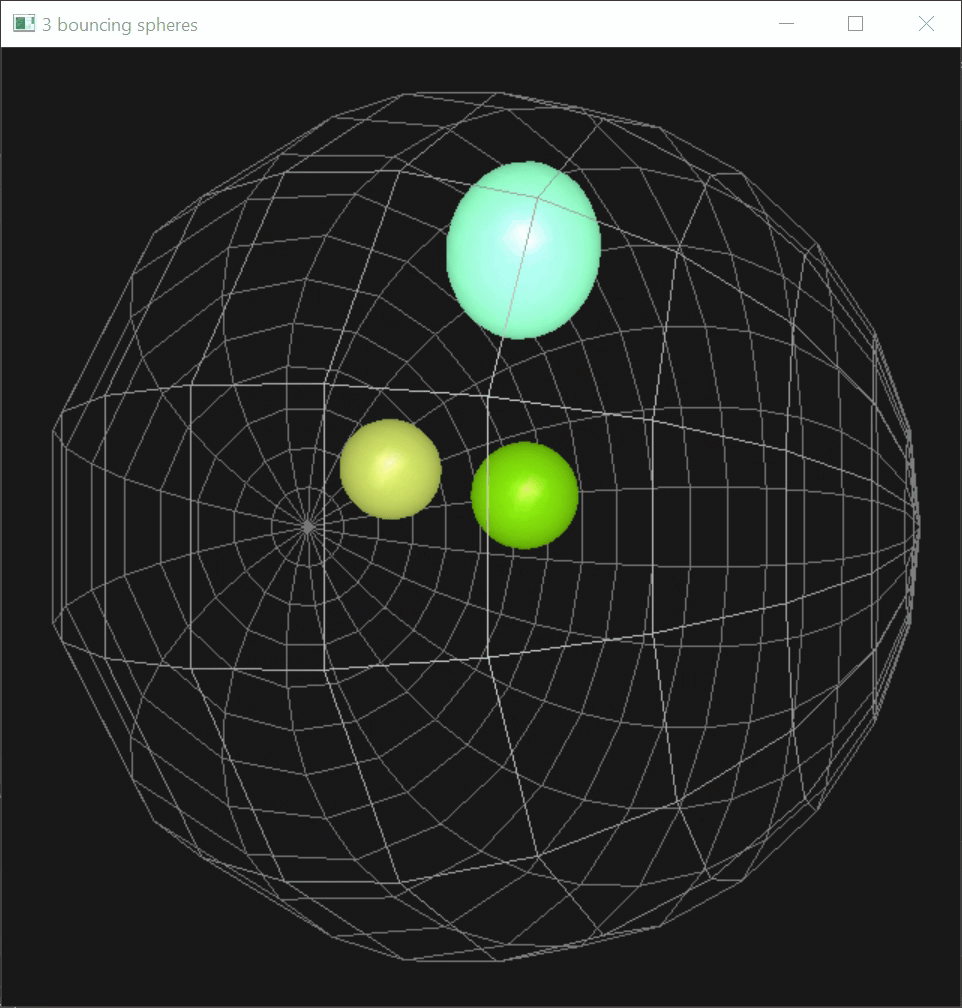
I contained three rigid spheres inside of a bigger, rigid wire sphere. Each sphere is given a random velocity in a random direction, and my code handles all collisions between the bouncing spheres as well as between the spheres and the spherical container.

Here's how the bouncing spheres look:

Cursor Interactions

Building upon the sphere collision setup (above), I implemented drag-and-drop using mouse cursor. This consisted of 3 steps:

1. Identifying the selected object.
2. Tracking the the cursor position.
3. Releasing the object at the correct location.

To select an object with a cursor left-click, I made use of the Stencil Buffer. By using the glutMouseFunc with a callback function that accesses which stencil the cursor clicked on, I appropriately selected the object to be moved.

Next, I used the glutPassiveMouseFunc, which passively calls a callback function which accesses the cursor's screen coordinates. I mapped the screen coordinates of the cursor to the world coordinates of the selected object in such a way that the object cannot escape its confinement.

The callback function within glutMouseFunc identifies when the object is released, and it is allowed to move freely with its previous velocity. The object while paused still has the ability to interact with other objects in the form of collisions.

Apart from cursor interactions, I implemented rotation and scaling of the objects as well. These actions work when the object is paused or when the object is held/selected:

• Pressing Q and E rotates the object in opposite directions about a random axis passing throught the centroid of the object.
• Using + and - scales the objects.

Here's a small demo: