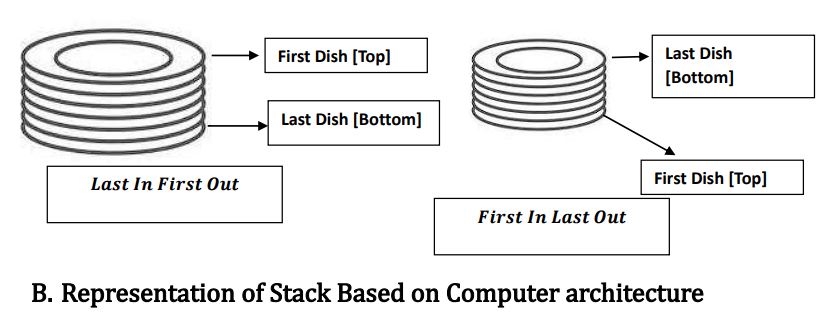
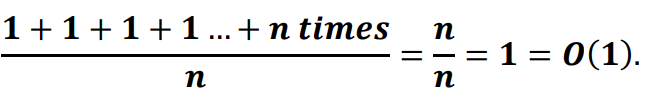𝑫𝒆𝒇𝒊𝒏𝒊𝒕𝒊𝒐𝒏: - 𝑨 𝒔𝒕𝒂𝒄𝒌 𝒊𝒔 𝒂𝒏 𝒐𝒓𝒅𝒆𝒓𝒆𝒅 𝒍𝒊𝒔𝒕 (𝒊. 𝒆. ,𝒍𝒊𝒔𝒕𝒆𝒅 𝒊𝒏 𝒂 𝒔𝒑𝒆𝒄𝒊𝒇𝒊𝒄 𝒐𝒓𝒅𝒆𝒓 (𝒐𝒓𝒅𝒆𝒓𝒆𝒅))𝒊𝒏 𝒘𝒉𝒊𝒄𝒉 𝒊𝒏𝒔𝒆𝒓𝒕𝒊𝒐𝒏 𝒂𝒏𝒅 𝒅𝒆𝒍𝒆𝒕𝒊𝒐𝒏 𝒂𝒓𝒆 𝒅𝒐𝒏𝒆 𝒂𝒕 𝒐𝒏𝒆 𝒆𝒏𝒅, 𝒄𝒂𝒍𝒍𝒆𝒅 𝒕𝒐𝒑.

𝑰𝒇 𝒘𝒆 𝒕𝒂𝒌𝒆 𝒕𝒉𝒆 𝒆𝒙𝒂𝒎𝒑𝒍𝒆 𝒐𝒇 𝑫𝒊𝒔𝒉, 𝒘𝒉𝒊𝒍𝒆 𝒂𝒓𝒓𝒂𝒏𝒈𝒊𝒏𝒈 𝒕𝒉𝒆 𝒔𝒕𝒂𝒄𝒌 𝒐𝒇 𝒅𝒊𝒔𝒉𝒆𝒔, 𝒘𝒆 𝒌𝒆𝒆𝒑 𝒐𝒏𝒆 𝒅𝒊𝒔𝒉 𝒖𝒑𝒐𝒏 𝒂𝒏𝒐𝒕𝒉𝒆𝒓 𝒊.𝒆., 𝒕𝒉𝒆 𝒎𝒆𝒄𝒉𝒂𝒏𝒊𝒔𝒎 𝒄𝒂𝒍𝒍𝒆𝒅 “𝑳𝒂𝒔𝒕 𝑰𝒏” 𝒂𝒏𝒅 𝒏𝒐𝒘 𝒊𝒇 𝒘𝒆 𝒘𝒂𝒏𝒕 𝒕𝒐 𝒓𝒆𝒎𝒐𝒗𝒆 𝒂 𝒅𝒊𝒔𝒉 𝒘𝒆 𝒔𝒉𝒐𝒖𝒍𝒅 𝒓𝒆𝒎𝒐𝒗𝒆 𝒕𝒉𝒆 𝒇𝒊𝒓𝒔𝒕 𝒅𝒊𝒔𝒉, 𝒕𝒉𝒊𝒔 𝒎𝒆𝒄𝒉𝒂𝒏𝒊𝒔𝒎 𝒊𝒔 𝒄𝒂𝒍𝒍𝒆𝒅 “𝑭𝒊𝒓𝒔𝒕 𝑶𝒖𝒕”, 𝒉𝒆𝒏𝒄𝒆 𝒘𝒉𝒐𝒍𝒆 𝒎𝒆𝒄𝒉𝒂𝒏𝒊𝒔𝒎 𝒊𝒔 𝒄𝒂𝒍𝒍𝒆𝒅: “𝑳𝒂𝒔𝒕 𝒊𝒏 𝑭𝒊𝒓𝒔𝒕 𝑶𝒖𝒕”. 𝑶𝒓 𝒊𝒇 𝒘𝒆 𝒔𝒂𝒚 𝒍𝒂𝒔𝒕 𝒅𝒊𝒔𝒉 𝒊𝒔 𝑭𝒊𝒓𝒔𝒕 𝑫𝒊𝒔𝒉 𝒂𝒏𝒅 𝑭𝒊𝒓𝒔𝒕 𝑫𝒊𝒔𝒉 𝒂𝒔 𝑳𝒂𝒔𝒕 𝑫𝒊𝒔𝒉, 𝒊𝒕 𝒘𝒊𝒍𝒍 𝒃𝒆𝒄𝒐𝒎𝒆 “𝑭𝒊𝒓𝒔𝒕 𝑰𝒏 𝑳𝒂𝒔𝒕 𝑶𝒖𝒕” 𝒎𝒆𝒄𝒉𝒂𝒏𝒊𝒔𝒎.
- 1. 𝑷𝒓𝒐𝒈𝒓𝒂𝒎 𝑪𝒐𝒖𝒏𝒕𝒆𝒓 : - 𝑰𝒕 𝒊𝒔 𝒂 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒕𝒉𝒂𝒕 𝒎𝒂𝒏𝒂𝒈𝒆𝒔 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒐𝒇 𝒕𝒉𝒆 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏𝒔 𝒕𝒉𝒂𝒕 𝒕𝒐 𝒃𝒆 𝒆𝒙𝒆𝒄𝒖𝒕𝒆𝒅 𝒏𝒆𝒙𝒕. 𝑻𝒉𝒂𝒕 𝒊𝒔 𝒔𝒊𝒎𝒑𝒍𝒚 𝒂 𝒎𝒂𝒏𝒂𝒈𝒆𝒓 𝒘𝒉𝒊𝒄𝒉 𝒕𝒆𝒍𝒍𝒔 𝑪𝑷𝑼 𝒕𝒉𝒂𝒕 𝒘𝒉𝒂𝒕 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝒕𝒐 𝒃𝒆 𝒆𝒙𝒆𝒄𝒖𝒕𝒆𝒅.
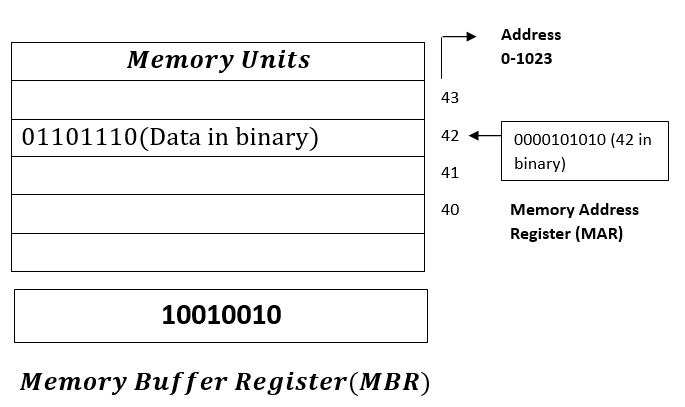
- 1. 𝑻𝒉𝒆 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏 𝒕𝒓𝒂𝒏𝒔𝒇𝒆𝒓 𝒕𝒐 𝒂𝒏𝒅 𝒇𝒓𝒐𝒎 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓𝒔 𝒊𝒏 𝒎𝒆𝒎𝒐𝒓𝒚 𝒂𝒏𝒅 𝒕𝒉𝒆 𝒆𝒙𝒕𝒆𝒓𝒏𝒂𝒍 𝒆𝒏𝒗𝒊𝒓𝒐𝒏𝒎𝒆𝒏𝒕 𝒊𝒔 𝒄𝒐𝒎𝒎𝒖𝒏𝒊𝒄𝒂𝒕𝒆𝒅 𝒕𝒉𝒓𝒐𝒖𝒈𝒉 𝒐𝒏𝒆 𝒄𝒐𝒎𝒎𝒐𝒏 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒄𝒂𝒍𝒍𝒆𝒅 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒃𝒖𝒇𝒇𝒆𝒓 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 (𝒐𝒕𝒉𝒆𝒓 𝒏𝒂𝒎𝒆𝒔 𝒂𝒓𝒆 𝒅𝒂𝒕𝒂 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓, 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒂𝒏𝒅 𝒔𝒕𝒐𝒓𝒂𝒈𝒆 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓).
- 2.𝑾𝒉𝒆𝒏 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒖𝒏𝒊𝒕 𝒓𝒆𝒄𝒆𝒊𝒗𝒆𝒔 𝒂 𝒘𝒓𝒊𝒕𝒆 𝒄𝒐𝒏𝒕𝒓𝒐𝒍 𝒔𝒊𝒈𝒏𝒂𝒍, 𝒕𝒉𝒆, 𝒊𝒏𝒕𝒆𝒓𝒏𝒂𝒍 𝒄𝒐𝒏𝒕𝒓𝒐𝒍 𝒊𝒏𝒕𝒆𝒓𝒑𝒓𝒆𝒕𝒔 𝒕𝒉𝒆 𝒄𝒐𝒏𝒕𝒆𝒏𝒕𝒔 𝒐𝒇 𝒕𝒉𝒆 𝒃𝒖𝒇𝒇𝒆𝒓 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒕𝒐 𝒃𝒆 𝒕𝒉𝒆 𝒃𝒊𝒕 𝒄𝒐𝒏𝒇𝒊𝒈𝒖𝒓𝒂𝒕𝒊𝒐𝒏 𝒐𝒇 𝒕𝒉𝒆 𝒘𝒐𝒓𝒅 𝒕𝒐 𝒃𝒆 𝒔𝒕𝒐𝒓𝒆𝒅 𝒊𝒏 𝒂 𝒎𝒆𝒎𝒐𝒓𝒚 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓.
- 3.𝑾𝒊𝒕𝒉 𝒂 𝒓𝒆𝒂𝒅 𝒄𝒐𝒏𝒕𝒓𝒐𝒍 𝒔𝒊𝒈𝒏𝒂𝒍, 𝒕𝒉𝒆 𝒊𝒏𝒕𝒆𝒓𝒏𝒂𝒍 𝒄𝒐𝒏𝒕𝒓𝒐𝒍 𝒔𝒆𝒏𝒅𝒔 𝒕𝒉𝒆 𝒘𝒐𝒓𝒅 𝒇𝒓𝒐𝒎 𝒂 𝒎𝒆𝒎𝒐𝒓𝒚 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒊𝒏𝒕𝒐 𝒕𝒉𝒆 𝒃𝒖𝒇𝒇𝒆𝒓 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓.
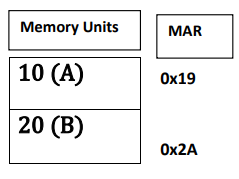
- 4.𝑰𝒏 𝒆𝒂𝒄𝒉 𝒄𝒂𝒔𝒆 𝒕𝒉𝒆 𝒄𝒐𝒏𝒕𝒆𝒏𝒕𝒔 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒔𝒑𝒆𝒄𝒊𝒇𝒚 𝒕𝒉𝒆 𝒑𝒂𝒓𝒕𝒊𝒄𝒖𝒍𝒂𝒓 𝒎𝒆𝒎𝒐𝒓𝒚 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒓𝒆𝒇𝒆𝒓𝒆𝒏𝒄𝒆𝒅 𝒇𝒐𝒓 𝒘𝒓𝒊𝒕𝒊𝒏𝒈 𝒐𝒓 𝒓𝒆𝒂𝒅𝒊𝒏𝒈.

𝑪𝒐𝒏𝒔𝒊𝒅𝒆𝒓 𝒂 𝒎𝒆𝒎𝒐𝒓𝒚 𝒖𝒏𝒊𝒕 𝒐𝒇 1024 𝒘𝒐𝒓𝒅𝒔 𝒘𝒊𝒕𝒉 8 𝒃𝒊𝒕𝒔 𝒑𝒆𝒓 𝒘𝒐𝒓𝒅. 𝑻𝒐 𝒔𝒑𝒆𝒄𝒊𝒇𝒚 1024 𝒘𝒐𝒓𝒅𝒔, 𝒘𝒆 𝒏𝒆𝒆𝒅 𝒂𝒏 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒐𝒇 10 𝒃𝒊𝒕𝒔, 𝒔𝒊𝒏𝒄𝒆 2^10=1024. 𝑯𝒆𝒏𝒄𝒆 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒉𝒂𝒔 1024 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓𝒔 𝒘𝒊𝒕𝒉 𝒂𝒔𝒔𝒊𝒈𝒏𝒆𝒅 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒏𝒖𝒎𝒃𝒆𝒓𝒔 𝒇𝒓𝒐𝒎 0 𝒕𝒐 1023.
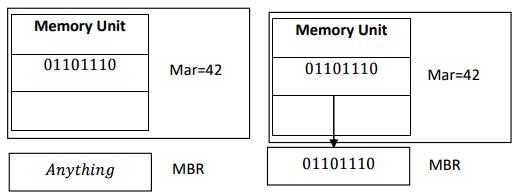
𝑨 𝒅𝒆𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒗𝒆 𝒓𝒆𝒂𝒅 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒕𝒓𝒂𝒏𝒔𝒇𝒆𝒓𝒔 𝒕𝒉𝒆 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒘𝒐𝒓𝒅 𝒊𝒏𝒕𝒐 𝑴𝑩𝑹 𝒃𝒖𝒕 𝒍𝒆𝒂𝒗𝒆𝒔 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒘𝒊𝒕𝒉 𝒂𝒍𝒍 0’𝒔. 𝑵𝒐𝒓𝒎𝒂𝒍 𝒎𝒆𝒎𝒐𝒓𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒓𝒆𝒒𝒖𝒊𝒓𝒆𝒔 𝒕𝒉𝒂𝒕 𝒕𝒉𝒆 𝒄𝒐𝒏𝒕𝒆𝒏𝒕 𝒐𝒇 𝒕𝒉𝒆 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒘𝒐𝒓𝒅 𝒓𝒆𝒎𝒂𝒊𝒏 𝒊𝒏 𝒎𝒆𝒎𝒐𝒓𝒚 𝒂𝒇𝒕𝒆𝒓 𝒂 𝒓𝒆𝒂𝒅 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏. 𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝒊𝒕 𝒊𝒔 𝒏𝒆𝒄𝒆𝒔𝒔𝒂𝒓𝒚 𝒕𝒐 𝒈𝒐 𝒕𝒉𝒓𝒐𝒖𝒈𝒉 𝒂 𝒓𝒆𝒔𝒕𝒐𝒓𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒕𝒉𝒂𝒕 𝒘𝒓𝒊𝒕𝒆𝒔 𝒕𝒉𝒆 𝒗𝒂𝒍𝒖𝒆 𝒊𝒏 𝑴𝑩𝑹 𝒊𝒏𝒕𝒐 𝒕𝒉𝒆 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒎𝒆𝒎𝒐𝒓𝒚 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓. 𝑫𝒖𝒓𝒊𝒏𝒈 𝒕𝒉𝒆 𝒓𝒆𝒔𝒕𝒐𝒓𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏, 𝒕𝒉𝒆 𝒄𝒐𝒏𝒕𝒆𝒏𝒕𝒔 𝒐𝒇 𝑴𝑨𝑹 𝒂𝒏𝒅 𝑴𝑩𝑹 𝒎𝒖𝒔𝒕 𝒓𝒆𝒎𝒂𝒊𝒏 𝒖𝒏𝒄𝒉𝒂𝒏𝒈𝒆𝒅.
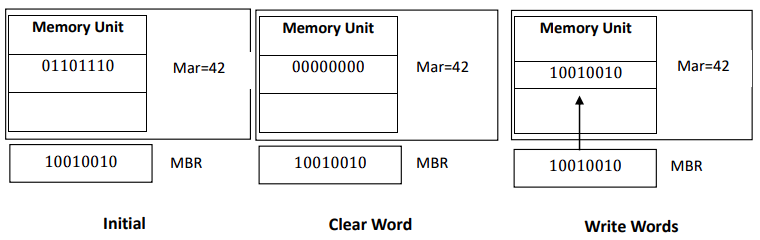
𝑨 𝒘𝒓𝒊𝒕𝒆 𝒄𝒐𝒏𝒕𝒓𝒐𝒍 𝒊𝒏𝒑𝒖𝒕 𝒂𝒑𝒑𝒍𝒊𝒆𝒅 𝒕𝒐 𝒂 𝒎𝒂𝒈𝒏𝒆𝒕𝒊𝒄-𝒄𝒐𝒓𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒄𝒂𝒖𝒔𝒆𝒔 𝒂 𝒕𝒓𝒂𝒏𝒔𝒇𝒆𝒓 𝒐𝒇 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏. 𝑻𝒐 𝒕𝒓𝒂𝒏𝒔𝒇𝒆𝒓 𝒏𝒆𝒘 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏 𝒊𝒏𝒕𝒐 𝒂 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓, 𝒕𝒉𝒆 𝒐𝒍𝒅 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏 𝒎𝒖𝒔𝒕 𝒇𝒊𝒓𝒔𝒕 𝒃𝒆 𝒆𝒓𝒂𝒔𝒆𝒅 𝒃𝒚 𝒄𝒍𝒆𝒂𝒓𝒊𝒏𝒈 𝒂𝒍𝒍 𝒕𝒉𝒆 𝒃𝒊𝒕𝒔 𝒐𝒇 𝒕𝒉𝒆 𝒘𝒐𝒓𝒅 𝒕𝒐 0. 𝑨𝒇𝒕𝒆𝒓 𝒕𝒉𝒊𝒔 𝒅𝒐𝒏𝒆, 𝒕𝒉𝒆 𝒄𝒐𝒏𝒕𝒆𝒏𝒕 𝒐𝒇 𝒕𝒉𝒆 𝑴𝑩𝑹 𝒄𝒂𝒏 𝒃𝒆 𝒕𝒓𝒂𝒏𝒔𝒇𝒆𝒓𝒓𝒆𝒅 𝒕𝒐 𝒕𝒉𝒆 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒘𝒐𝒓𝒅. 𝑴𝑨𝑹 𝒎𝒖𝒔𝒕 𝒏𝒐𝒕 𝒄𝒉𝒂𝒏𝒈𝒆 𝒅𝒖𝒓𝒊𝒏𝒈 𝒕𝒉𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒕𝒐 𝒆𝒏𝒔𝒖𝒓𝒆 𝒕𝒉𝒂𝒕 𝒕𝒉𝒆 𝒔𝒂𝒎𝒆 𝒔𝒆𝒍𝒆𝒄𝒕𝒆𝒅 𝒘𝒐𝒓𝒅 𝒕𝒉𝒂𝒕 𝒊𝒔 𝒄𝒍𝒆𝒂𝒓𝒆𝒅 𝒊𝒔 𝒕𝒉𝒆 𝒐𝒏𝒆 𝒕𝒉𝒂𝒕 𝒓𝒆𝒄𝒆𝒊𝒗𝒆𝒔 𝒕𝒉𝒆 𝒏𝒆𝒘 𝒊𝒏𝒇𝒐𝒓𝒎𝒂𝒕𝒊𝒐𝒏.
𝑻𝒉𝒆 𝒐𝒑𝒆𝒓𝒂𝒏𝒅𝒔 𝒂𝒓𝒆 𝒕𝒉𝒐𝒔𝒆 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 𝒕𝒉𝒂𝒕 𝒂𝒓𝒆 𝒘𝒐𝒓𝒌𝒆𝒅 𝒃𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒐𝒓 𝒕𝒐 𝒑𝒓𝒐𝒅𝒖𝒄𝒆 𝒂 𝒓𝒆𝒔𝒖𝒍𝒕 𝒂𝒏𝒅 𝒔𝒖𝒄𝒉 𝒂𝒅𝒅𝒓𝒆𝒔𝒔𝒆𝒔 𝒐𝒇 𝒐𝒑𝒆𝒓𝒂𝒏𝒅𝒔 𝒂𝒓𝒆 𝒔𝒕𝒐𝒓𝒆𝒅 𝒊𝒏 𝒅𝒂𝒕𝒂 𝒐𝒑𝒆𝒓𝒂𝒏𝒅𝒔 𝒔𝒆𝒄𝒕𝒊𝒐𝒏 𝒐𝒇 𝒎𝒆𝒎𝒐𝒓𝒚.
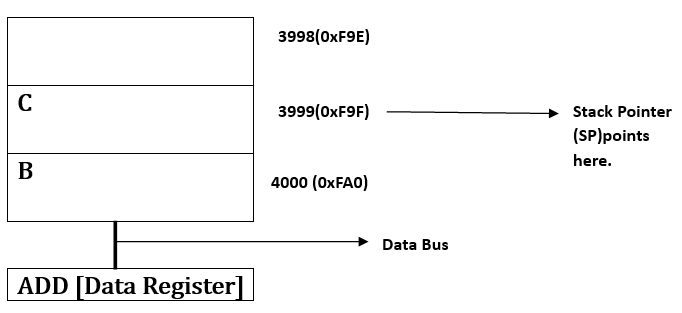
- 3. 𝑻𝒉𝒆 𝒐𝒑𝒆𝒓𝒂𝒏𝒅 𝒅𝒂𝒕𝒂 𝒈𝒆𝒕𝒔 𝒔𝒕𝒐𝒓𝒆𝒅 𝒊𝒏 𝑫𝒂𝒕𝒂 𝑶𝒑𝒆𝒓𝒂𝒏𝒅 𝒔𝒆𝒄𝒕𝒊𝒐𝒏 𝒂𝒔 𝒔𝒉𝒐𝒘𝒏 𝒂𝒃𝒐𝒗𝒆 𝒂𝒏𝒅 𝑴𝑨𝑹 𝒘𝒊𝒍𝒍 𝒉𝒐𝒍𝒅 𝒕𝒉𝒆 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒂𝒏𝒅 𝑴𝑩𝑹 𝒘𝒊𝒍𝒍 𝒉𝒐𝒍𝒅 𝒕𝒉𝒆 𝒅𝒂𝒕𝒂 𝒊.𝒆., 𝒄𝒐𝒏𝒕𝒆𝒏𝒕 𝒐𝒇 𝒕𝒉𝒆 𝒎𝒆𝒎𝒐𝒓𝒚 𝒊𝒏 𝒘𝒐𝒓𝒅 𝒘𝒉𝒊𝒍𝒆 𝒘𝒆 𝒑𝒓𝒐𝒄𝒆𝒔𝒔 𝒕𝒉𝒆 𝒅𝒂𝒕𝒂.
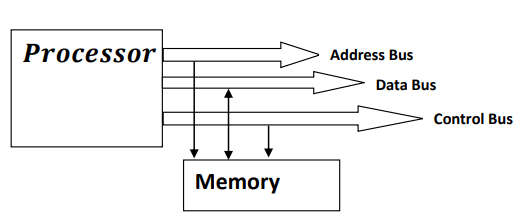
- 4. 𝑻𝒉𝒆𝒓𝒆 𝒊𝒔 𝒂𝒏𝒐𝒕𝒉𝒆𝒓 𝒓𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝒕𝒉𝒆 𝑪𝑷𝑼 𝒕𝒉𝒂𝒕 𝒊𝒔 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 (𝑰𝑹) 𝒘𝒉𝒊𝒄𝒉 𝒓𝒆𝒄𝒆𝒊𝒗𝒆𝒔 𝒕𝒉𝒆𝒔𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒄𝒐𝒅𝒆 𝒐𝒇 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏𝒔 𝒄𝒐𝒎𝒎𝒖𝒏𝒊𝒄𝒂𝒕𝒆𝒅 𝒕𝒉𝒓𝒐𝒖𝒈𝒉 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒃𝒖𝒔 𝒄𝒐𝒏𝒏𝒆𝒄𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝑷𝒓𝒐𝒈𝒓𝒂𝒎 𝑪𝒐𝒖𝒏𝒕𝒆𝒓 (𝑷𝑪) 𝒘𝒉𝒊𝒄𝒉 𝒉𝒐𝒍𝒅𝒔 𝒂𝒅𝒅𝒓𝒆𝒔𝒔𝒆𝒔 𝒐𝒇 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒄𝒐𝒅𝒆 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏𝒔 𝒂𝒏𝒅 𝒕𝒉𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔 𝒄𝒂𝒏 𝒃𝒆 𝒅𝒆𝒇𝒊𝒏𝒆𝒅 𝒂𝒔: 𝑨𝑫𝑫 (𝑨𝒅𝒅𝒊𝒕𝒊𝒐𝒏), 𝑺𝑼𝑩 (𝑺𝒖𝒃𝒕𝒓𝒂𝒄𝒕𝒊𝒐𝒏), 𝑴𝑼𝑳 (𝑴𝒖𝒍𝒕𝒊𝒑𝒍𝒊𝒄𝒂𝒕𝒊𝒐𝒏), 𝒆𝒕𝒄. 𝒂𝒏𝒅 𝒕𝒉𝒆 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒘𝒉𝒊𝒄𝒉 𝒘𝒊𝒍𝒍 𝒃𝒆 𝒅𝒐𝒏𝒆 𝒘𝒊𝒕𝒉 𝒐𝒑𝒆𝒓𝒂𝒏𝒅𝒔 𝒔𝒖𝒄𝒉 𝒂𝒅𝒅𝒓𝒆𝒔𝒔𝒆𝒔 𝒊𝒔 𝒇𝒆𝒕𝒄𝒉𝒆𝒅 𝒃𝒚 𝑴𝑨𝑹 (𝑴𝒆𝒎𝒐𝒓𝒚 𝑨𝒅𝒅𝒓𝒆𝒔𝒔 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓) 𝒂𝒏𝒅 𝒂 𝒅𝒆𝒄𝒐𝒅𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 (𝑰𝑹) 𝒔𝒖𝒑𝒑𝒍𝒊𝒆𝒔 𝒆𝒂𝒄𝒉 𝒐𝒖𝒕𝒑𝒖𝒕 𝒕𝒐 𝒕𝒉𝒆 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 .
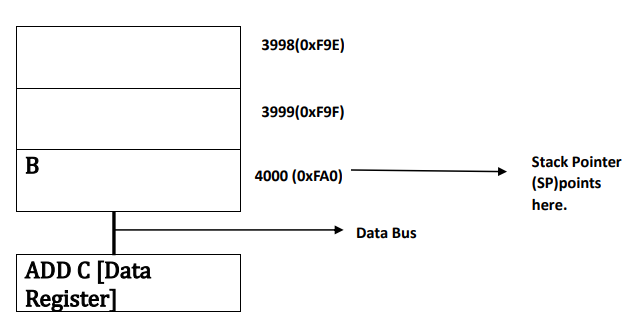
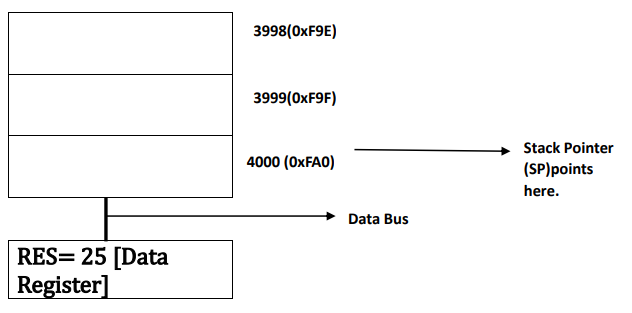
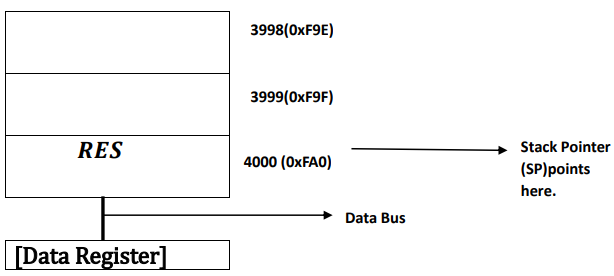
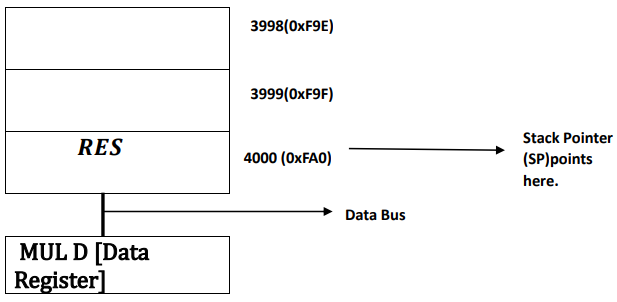
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝑺𝒕𝒂𝒄𝒌 𝑷𝒐𝒊𝒏𝒕𝒆𝒓 𝒑𝒐𝒊𝒏𝒕𝒔 𝒂𝒕 𝒕𝒉𝒆 𝒍𝒂𝒔𝒕 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 4000, 𝑾𝒉𝒊𝒍𝒆 𝒕𝒉𝒆 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝒈𝒆𝒕𝒔 𝒄𝒐𝒎𝒑𝒍𝒆𝒕𝒆𝒅 𝒊.𝒆. 𝑨𝑫𝑫 𝑪,𝑩 (=13+12)𝒂𝒏𝒅 𝒊𝒕 𝒈𝒐𝒆𝒔 𝒕𝒐 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝒊𝒕𝒔 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒂𝒏𝒅 𝒅𝒆𝒄𝒐𝒅𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒐𝒇 𝑪𝑷𝑼 𝒑𝒓𝒐𝒗𝒊𝒅𝒆𝒔 𝒕𝒉𝒆 𝒐𝒖𝒕 𝒑𝒖𝒕 , 𝒔𝒂𝒚 𝒐𝒖𝒕𝒑𝒖𝒕 = 𝑹𝑬𝑺(=25) . 𝑻𝒉𝒆 𝒗𝒂𝒍𝒖𝒆 𝒈𝒆𝒕𝒔 𝒂𝒈𝒂𝒊𝒏 𝒔𝒕𝒐𝒓𝒆𝒅 𝒂𝒕 𝑫𝒂𝒕𝒂 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓.
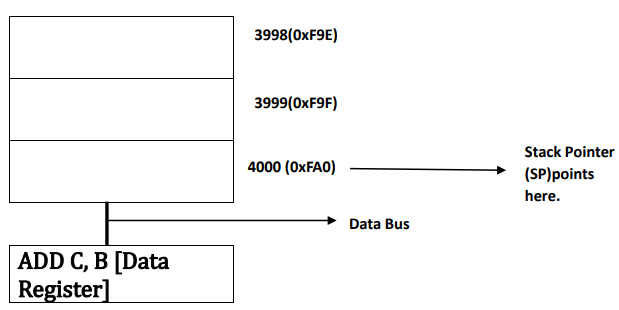
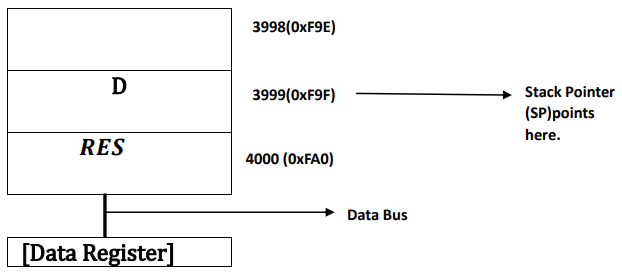
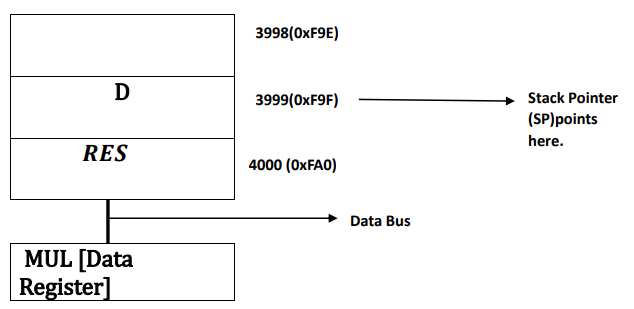
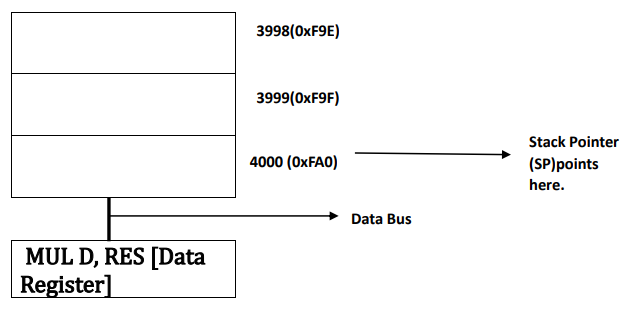
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆, 𝑺𝒕𝒂𝒄𝒌 𝑷𝒐𝒊𝒏𝒕𝒆𝒓 𝒑𝒐𝒊𝒏𝒕𝒔 𝒂𝒕 𝒕𝒉𝒆 𝒍𝒂𝒔𝒕 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 4000, 𝑾𝒉𝒊𝒍𝒆 𝒕𝒉𝒆 𝒊𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝒈𝒆𝒕𝒔 𝒄𝒐𝒎𝒑𝒍𝒆𝒕𝒆𝒅 𝒊.𝒆., 𝑴𝑼𝑳 𝑫, 𝑹𝑬𝑺 (=10×25=250)𝒂𝒏𝒅 𝒊𝒕 𝒈𝒐𝒆𝒔 𝒕𝒐 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝒊𝒕𝒔 𝒂𝒅𝒅𝒓𝒆𝒔𝒔 𝒂𝒏𝒅 𝒅𝒆𝒄𝒐𝒅𝒆𝒓 𝒂𝒔𝒔𝒐𝒄𝒊𝒂𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝑰𝒏𝒔𝒕𝒓𝒖𝒄𝒕𝒊𝒐𝒏 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒐𝒇 𝑪𝑷𝑼 𝒑𝒓𝒐𝒗𝒊𝒅𝒆𝒔 𝒕𝒉𝒆 𝒐𝒖𝒕𝒑𝒖𝒕. 𝑻𝒉𝒆 𝒗𝒂𝒍𝒖𝒆 𝒈𝒆𝒕𝒔 𝒂𝒈𝒂𝒊𝒏 𝒔𝒕𝒐𝒓𝒆𝒅 𝒂𝒕 𝑫𝒂𝒕𝒂 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓 𝒂𝒏𝒅 𝒕𝒉𝒆𝒏 𝒊𝒕 𝒈𝒆𝒕𝒔 𝒊𝒏𝒕𝒆𝒓𝒑𝒓𝒆𝒕𝒆𝒅 𝒕𝒐 𝒖𝒔𝒆𝒓.
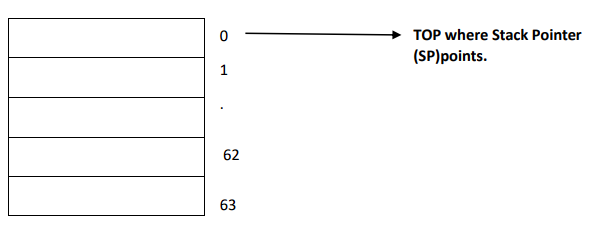
𝑳𝒆𝒕𝒔 𝒔𝒂𝒚 0 𝒊𝒔 𝒕𝒐𝒑 𝒕𝒉𝒆𝒏 𝑷𝒖𝒔𝒉 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒐𝒄𝒄𝒖𝒓𝒔: 𝑺𝑷 = 𝑺𝑷+1 (𝑰𝒏𝒄𝒓𝒆𝒎𝒆𝒏𝒕 𝒐𝒇 𝑺𝒕𝒂𝒄𝒌 𝑷𝒐𝒊𝒏𝒕𝒆𝒓) 𝒂𝒏𝒅 𝑷𝑶𝑷 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒐𝒄𝒄𝒖𝒓𝒔: 𝑺𝑷 = 𝑺𝑷-1 (𝑫𝒆𝒄𝒓𝒆𝒎𝒆𝒏𝒕 𝒐𝒇 𝑺𝒕𝒂𝒄𝒌 𝑷𝒐𝒊𝒏𝒕𝒆𝒓). 63 𝒊𝒔 𝒕𝒉𝒆 𝒍𝒂𝒔𝒕 𝒃𝒊𝒕 𝒓𝒆𝒑𝒓𝒆𝒔𝒆𝒏𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝑩𝒊𝒏𝒂𝒓𝒚 𝒅𝒊𝒈𝒊𝒕𝒔 111111 (𝑺𝒊𝒙 𝑶𝒏𝒆𝒔=𝑺𝒊𝒙 𝑩𝒊𝒕𝒔). 𝑻𝒉𝒆𝒏 𝒕𝒉𝒆 𝒕𝒐𝒑 0 𝒘𝒊𝒍𝒍 𝒃𝒆 𝒓𝒆𝒑𝒓𝒆𝒔𝒆𝒏𝒕𝒆𝒅 𝒊𝒏 6 𝒃𝒊𝒕𝒔 𝒐𝒓 6 𝒛𝒆𝒓𝒐𝒆𝒔 [000 000].
𝑻𝒉𝒆𝒓𝒆𝒇𝒐𝒓𝒆 𝒘𝒉𝒆𝒏 𝒊𝒕 𝒓𝒆𝒂𝒄𝒉𝒆𝒔 0, 𝒏𝒆𝒙𝒕 𝒅𝒆𝒄𝒓𝒆𝒎𝒆𝒏𝒕 𝒘𝒊𝒍𝒍 𝒄𝒂𝒖𝒔𝒆 : -1 , 𝑹𝒆𝒑𝒓𝒆𝒔𝒆𝒏𝒕𝒂𝒕𝒊𝒐𝒏 𝒐𝒇 6 𝒃𝒊𝒕 𝒐𝒇 1 = 000 001 , 𝑶𝒏𝒆’𝒔 𝒄𝒐𝒎𝒑𝒍𝒆𝒎𝒆𝒏𝒕 𝒐𝒇 1 = 111 110 𝒂𝒏𝒅 𝑻𝒘𝒐’𝒔 𝒄𝒐𝒎𝒑𝒍𝒆𝒎𝒆𝒏𝒕 (111 110 +1) = 111 111. 𝑨𝒏𝒅 𝒘𝒆 𝒌𝒏𝒐𝒘 111 111 𝒊𝒔 63 , 𝒉𝒆𝒏𝒄𝒆 𝒂𝒈𝒂𝒊𝒏 𝒔𝒕𝒂𝒄𝒌 𝒘𝒊𝒍𝒍 𝒑𝒐𝒊𝒏𝒕 𝒂𝒕 63.
𝑨𝒈𝒂𝒊𝒏, 𝒊𝒇 𝒘𝒆 𝒏𝒐𝒕𝒊𝒄𝒆, 𝑺𝒂𝒎𝒆 𝒘𝒂𝒚 𝑨 𝑹𝑬𝑮𝑰𝑺𝑻𝑬𝑹 𝑺𝑻𝑨𝑪𝑲 𝒘𝒐𝒓𝒌𝒔 𝒍𝒊𝒌𝒆 𝑴𝑬𝑴𝑶𝑹𝒀 𝑺𝑻𝑨𝑪𝑲 𝒂𝒔 𝑹𝒆𝒈𝒊𝒔𝒕𝒆𝒓𝒔 𝒂𝒓𝒆 𝒂𝒍𝒔𝒐 𝒂 𝒎𝒆𝒎𝒐𝒓𝒚 (𝒔𝒎𝒂𝒍𝒍𝒆𝒔𝒕 𝒅𝒂𝒕𝒂 𝒔𝒕𝒐𝒓𝒂𝒈𝒆 𝒖𝒏𝒊𝒕).
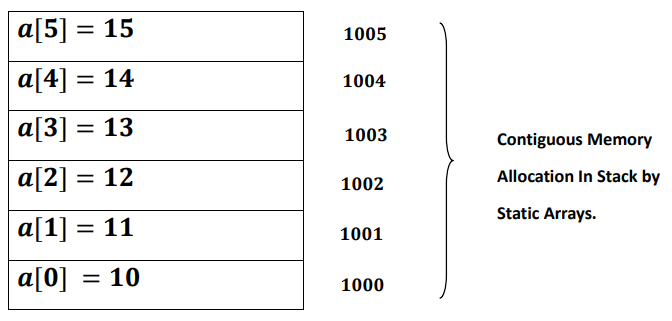
𝑻𝒉𝒆 𝒏𝒆𝒙𝒕 𝒂𝒓𝒓𝒂𝒚𝒔 𝒊𝒏𝒅𝒆𝒙 𝒘𝒊𝒍𝒍 𝒃𝒆 1001 𝒐𝒇 𝒔𝒕𝒂𝒄𝒌 𝒂𝒏𝒅 𝒏𝒐𝒕 1004 𝒐𝒓 𝒂𝒏𝒚 𝒐𝒕𝒉𝒆𝒓 𝒂𝒅𝒅𝒓𝒆𝒔𝒔. 𝑻𝒉𝒊𝒔 𝒊𝒔 𝒕𝒉𝒆 𝒄𝒐𝒏𝒄𝒆𝒑𝒕 𝒐𝒇 𝒄𝒐𝒏𝒕𝒊𝒈𝒖𝒐𝒖𝒔 𝒎𝒆𝒎𝒐𝒓𝒚 𝒂𝒍𝒍𝒐𝒄𝒂𝒕𝒊𝒐𝒏 𝒕𝒉𝒂𝒕 𝒊𝒔 𝒔𝒕𝒐𝒓𝒊𝒏𝒈 𝒊𝒏 𝒎𝒆𝒎𝒐𝒓𝒚 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕𝒍𝒚 𝒊𝒕 𝒍𝒐𝒐𝒌𝒔 𝒍𝒊𝒌𝒆:
𝑨𝒔 𝒘𝒆 𝒔𝒆𝒆 𝒃𝒐𝒕𝒉 𝒔𝒕𝒂𝒄𝒌 𝒂𝒏𝒅 𝑨𝒓𝒓𝒂𝒚𝒔 𝒂𝒓𝒆 𝒍𝒊𝒏𝒆𝒂𝒓𝒍𝒚 𝒔𝒕𝒓𝒖𝒄𝒕𝒖𝒓𝒆𝒅 , 𝒐𝒏𝒆 𝒂𝒇𝒕𝒆𝒓 𝒕𝒉𝒆 𝒐𝒕𝒉𝒆𝒓 𝒉𝒆𝒏𝒄𝒆 𝒕𝒉𝒆𝒚 𝒇𝒂𝒍𝒍 𝒊𝒏 𝒍𝒊𝒏𝒆𝒂𝒓 𝒅𝒂𝒕𝒂 𝒔𝒕𝒓𝒖𝒄𝒕𝒖𝒓𝒆 . 𝑻𝒉𝒂𝒕 𝒊𝒔 𝒆𝒂𝒄𝒉 𝒎𝒆𝒎𝒃𝒆𝒓 𝒊𝒔 𝒂𝒕𝒕𝒂𝒄𝒉𝒆𝒅 𝒕𝒐 𝒊𝒕𝒔 𝒏𝒆𝒊𝒈𝒉𝒃𝒐𝒓𝒊𝒏𝒈 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔. 𝑨𝒏𝒅 𝒘𝒆 𝒄𝒂𝒏 𝒓𝒆𝒑𝒓𝒆𝒔𝒆𝒏𝒕 𝒔𝒕𝒂𝒄𝒌 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒕𝒉𝒓𝒐𝒖𝒈𝒉 𝒂𝒓𝒓𝒂𝒚𝒔.

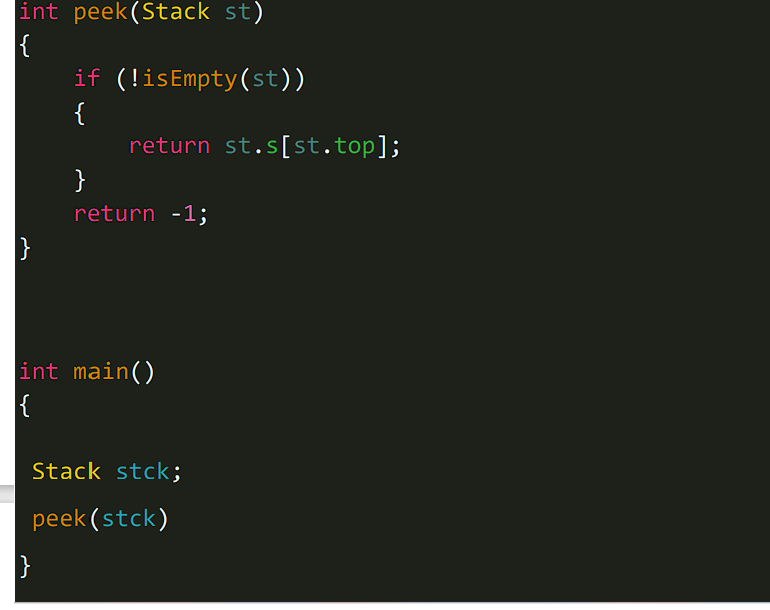
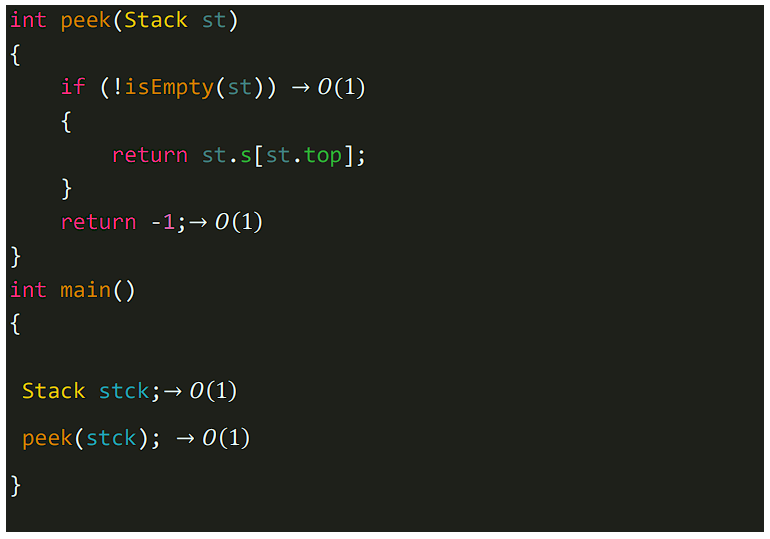
𝑵𝒐𝒘, 𝑶(1) 𝒊𝒔 𝒇𝒐𝒓 𝒔𝒊𝒏𝒈𝒍𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕 𝒘𝒉𝒂𝒕 𝒘𝒊𝒍𝒍 𝒃𝒆 𝒇𝒐𝒓 `𝒏` 𝒕𝒊𝒎𝒆𝒔 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒂𝒔 𝒘𝒆 𝒌𝒏𝒐𝒘 𝒏 𝒕𝒊𝒎𝒆𝒔 1=𝒏 ,𝒉𝒆𝒏𝒄𝒆 𝒊𝒕 𝒎𝒖𝒔𝒕 𝒈𝒆𝒏𝒆𝒓𝒂𝒕𝒆 𝑶(𝒏), 𝒃𝒖𝒕 𝒉𝒆𝒓𝒆 𝒘𝒆 𝒉𝒂𝒗𝒆 𝒂𝒏𝒂𝒍𝒚𝒛𝒆 𝒂𝒄𝒄𝒐𝒓𝒅𝒊𝒏𝒈 𝒕𝒐 𝑺𝒕𝒂𝒄𝒌 𝑶𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 .


𝑵𝒐𝒘, 𝑶(1) 𝒊𝒔 𝒇𝒐𝒓 𝒔𝒊𝒏𝒈𝒍𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕 𝒘𝒉𝒂𝒕 𝒘𝒊𝒍𝒍 𝒃𝒆 𝒇𝒐𝒓 `𝒏` 𝒕𝒊𝒎𝒆𝒔 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒂𝒔 𝒘𝒆 𝒌𝒏𝒐𝒘 𝒏 𝒕𝒊𝒎𝒆𝒔 1=𝒏 ,𝒉𝒆𝒏𝒄𝒆 𝒊𝒕 𝒎𝒖𝒔𝒕 𝒈𝒆𝒏𝒆𝒓𝒂𝒕𝒆 𝑶(𝒏), 𝒃𝒖𝒕 𝒉𝒆𝒓𝒆 𝒘𝒆 𝒉𝒂𝒗𝒆 𝒂𝒏𝒂𝒍𝒚𝒛𝒆 𝒂𝒄𝒄𝒐𝒓𝒅𝒊𝒏𝒈 𝒕𝒐 𝑺𝒕𝒂𝒄𝒌 𝑶𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 .
𝑳𝒆𝒕 𝒖𝒔 𝒊𝒎𝒑𝒓𝒐𝒗𝒆 𝒕𝒉𝒆 𝒄𝒐𝒎𝒑𝒍𝒆𝒙𝒊𝒕𝒚 𝒃𝒚 𝒖𝒔𝒊𝒏𝒈 𝒕𝒉𝒆 𝒂𝒓𝒓𝒂𝒚 𝒅𝒐𝒖𝒃𝒍𝒊𝒏𝒈 𝒕𝒆𝒄𝒉𝒏𝒊𝒒𝒖𝒆. 𝑰𝒇 𝒕𝒉𝒆 𝒂𝒓𝒓𝒂𝒚 𝒊𝒔 𝒇𝒖𝒍𝒍, 𝒄𝒓𝒆𝒂𝒕𝒆 𝒂 𝒏𝒆𝒘 𝒂𝒓𝒓𝒂𝒚 𝒐𝒇 𝒕𝒘𝒊𝒄𝒆 𝒕𝒉𝒆 𝒔𝒊𝒛𝒆 , 𝒂𝒏𝒅 𝒄𝒐𝒑𝒚 𝒕𝒉𝒆 𝒊𝒕𝒆𝒎𝒔 . 𝑾𝒊𝒕𝒉 𝒕𝒉𝒊𝒔 𝒂𝒑𝒑𝒓𝒐𝒂𝒄𝒉 , 𝒑𝒖𝒔𝒉𝒊𝒏𝒈 `𝒏` 𝒊𝒕𝒆𝒎𝒔 𝒕𝒂𝒌𝒆𝒔 𝒕𝒊𝒎𝒆 𝒑𝒓𝒐𝒑𝒐𝒓𝒕𝒊𝒐𝒏𝒂𝒍 𝒕𝒐 𝒏 (𝒏𝒐𝒕 𝒏^𝟐 ).
𝑭𝒐𝒓 𝒔𝒊𝒎𝒑𝒍𝒊𝒄𝒊𝒕𝒚 ,𝒍𝒆𝒕 𝒖𝒔 𝒂𝒔𝒔𝒖𝒎𝒆 𝒕𝒉𝒂𝒕 𝒊𝒏𝒊𝒕𝒊𝒂𝒍𝒍𝒚 𝒘𝒆 𝒔𝒕𝒂𝒓𝒕𝒆𝒅 𝒘𝒊𝒕𝒉 𝒏 = 𝟏 𝒂𝒏𝒅 𝒎𝒐𝒗𝒆𝒅 𝒖𝒑 𝒕𝒐 𝒏 = 𝟑𝟐 . 𝑻𝒉𝒂𝒕 𝒎𝒆𝒂𝒏𝒔 , 𝒘𝒆 𝒅𝒐 𝒕𝒉𝒆 𝒅𝒐𝒖𝒃𝒍𝒊𝒏𝒈 𝒂𝒕 𝟏, 𝟐, 𝟒, 𝟖, 𝟏𝟔. 𝑻𝒉𝒆 𝒐𝒕𝒉𝒆𝒓 𝒘𝒂𝒚 𝒐𝒇 𝒂𝒏𝒂𝒍𝒚𝒛𝒊𝒏𝒈 𝒕𝒉𝒆 𝒔𝒂𝒎𝒆 𝒂𝒑𝒑𝒓𝒐𝒂𝒄𝒉 𝒊𝒔: 𝒂𝒕 𝒏 = 𝟏 ,𝒊𝒇 𝒘𝒆 𝒘𝒂𝒏𝒕 𝒕𝒐 𝒂𝒅𝒅 (𝒑𝒖𝒔𝒉) 𝒂𝒏 𝒆𝒍𝒆𝒎𝒆𝒏𝒕 , 𝒅𝒐𝒖𝒃𝒍𝒆 𝒕𝒉𝒆 𝒄𝒖𝒓𝒓𝒆𝒏𝒕 𝒔𝒊𝒛𝒆 𝒐𝒇 𝒕𝒉𝒆 𝒂𝒓𝒓𝒂𝒚 𝒂𝒏𝒅 𝒄𝒐𝒑𝒚 𝒂𝒍𝒍 𝒕𝒉𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒐𝒇 𝒕𝒉𝒆 𝒐𝒍𝒅 𝒂𝒓𝒓𝒂𝒚 𝒕𝒐 𝒕𝒉𝒆 𝒏𝒆𝒘 𝒂𝒓𝒓𝒂𝒚.
𝑨𝒕 𝒏 = 𝟏 , 𝒘𝒆 𝒅𝒐 𝟏 𝒄𝒐𝒑𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 𝒂𝒕 𝒏 = 𝟐 , 𝒘𝒆 𝒅𝒐 𝟐 𝒄𝒐𝒑𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔, 𝒂𝒏𝒅 𝒂𝒕 𝒏 = 𝟒, 𝒘𝒆 𝒅𝒐 𝟒 𝒄𝒐𝒑𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔 𝒂𝒏𝒅 𝒔𝒐 𝒐𝒏. 𝑩𝒚 𝒕𝒉𝒆 𝒕𝒊𝒎𝒆 𝒘𝒆 𝒓𝒆𝒂𝒄𝒉 𝒏 = 𝟑𝟐, 𝒕𝒉𝒆 𝒕𝒐𝒕𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒄𝒐𝒑𝒚 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔 𝒊𝒔 𝟏 + 𝟐 + 𝟒 +𝟖 + 𝟏𝟔 = 𝟑𝟏 𝒘𝒉𝒊𝒄𝒉 𝒊𝒔 𝒂𝒑𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒕𝒆𝒍𝒚 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐 𝟐𝒏 𝒗𝒂𝒍𝒖𝒆(𝟑𝟐).
𝑾𝒆 𝒄𝒂𝒏 𝒔𝒆𝒆 𝒕𝒉𝒂𝒕 𝒕𝒉𝒆 𝒔𝒆𝒓𝒊𝒆𝒔 𝒘𝒆 𝒈𝒆𝒕 𝒊𝒔 ∶ 𝟐^𝟎 + 𝟐^𝟏 + 𝟐^𝟐 + 𝟐^𝟑 + 𝟐^𝟒 = 𝟑𝟏 𝒘𝒉𝒊𝒄𝒉 𝒊𝒔 𝒂𝒑𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒕𝒆𝒍𝒚 𝒆𝒒𝒖𝒂𝒍 𝒕𝒐 𝟐𝒏 𝒗𝒂𝒍𝒖𝒆(𝟑𝟐). 𝑰𝒇 𝒘𝒆 𝒐𝒃𝒔𝒆𝒓𝒗𝒆 𝒄𝒂𝒓𝒆𝒇𝒖𝒍𝒍𝒚, 𝒘𝒆 𝒂𝒓𝒆 𝒅𝒐𝒊𝒏𝒈 𝒕𝒉𝒆 𝒅𝒐𝒖𝒃𝒍𝒊𝒏𝒈 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏 `𝒍𝒐𝒈(𝒏)` 𝒕𝒊𝒎𝒆𝒔. 𝑵𝒐𝒘,𝒍𝒆𝒕 𝒖𝒔 𝒈𝒆𝒏𝒆𝒓𝒂𝒍𝒊𝒛𝒆 𝒕𝒉𝒆 𝒅𝒊𝒔𝒄𝒖𝒔𝒔𝒊𝒐𝒏. 𝑭𝒐𝒓 `𝒏` 𝒑𝒖𝒔𝒉 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔 𝒘𝒆 𝒅𝒐𝒖𝒃𝒍𝒆 𝒕𝒉𝒆 𝒂𝒓𝒓𝒂𝒚 𝒔𝒊𝒛𝒆 `𝒍𝒐𝒈(𝒏)` 𝒕𝒊𝒎𝒆𝒔. 𝑻𝒉𝒂𝒕 𝒎𝒆𝒂𝒏𝒔, 𝒘𝒆 𝒘𝒊𝒍𝒍 𝒉𝒂𝒗𝒆 `𝒍𝒐𝒈𝒏` 𝒕𝒆𝒓𝒎𝒔 𝒊𝒏 𝒕𝒉𝒆 𝒆𝒙𝒑𝒓𝒆𝒔𝒔𝒊𝒐𝒏 𝒃𝒆𝒍𝒐𝒘. 𝑻𝒉𝒆 𝒕𝒐𝒕𝒂𝒍 𝒕𝒊𝒎𝒆 𝑻(𝒏) 𝒐𝒇 𝒂 𝒔𝒆𝒓𝒊𝒆𝒔 𝒐𝒇 𝒏 𝒑𝒖𝒔𝒉 𝒐𝒑𝒆𝒓𝒂𝒕𝒊𝒐𝒏𝒔 𝒊𝒔 𝒑𝒓𝒐𝒑𝒐𝒓𝒕𝒊𝒐𝒏𝒂𝒍 𝒕𝒐:
$$\begin{equation}
\begin{split}
𝟏+𝟐+𝟒+𝟖....+ \dfrac{𝒏}{𝟒} + \dfrac{𝒏}{𝟐} + 𝒏 = 𝒏 + \dfrac{𝒏}{𝟐} + \dfrac{𝒏}{𝟒} +...𝟖+𝟒+𝟐+𝟏 \\\
= 𝑶(𝟐𝒏-𝒏(\dfrac{𝟏}{𝟐})^𝒏 ) = 𝑶(𝟐𝒏) = 𝑶(𝒏) \\
\end{split}
\end{equation}$$
𝟑. 𝑰𝒏 𝑷𝒖𝒔𝒉 , 𝒘𝒉𝒆𝒏 𝒕𝒉𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕 𝒊𝒔 𝒑𝒖𝒔𝒉𝒆𝒅 𝒊𝒏 𝑺𝒕𝒂𝒄𝒌 𝒕𝒉𝒆𝒏 𝒊𝒕𝒔 𝒄𝒉𝒆𝒄𝒌𝒆𝒅 𝒕𝒉𝒂𝒕 𝒊𝒇 𝒊𝒕𝒔 𝒇𝒖𝒍𝒍 𝒕𝒉𝒆𝒏 𝒅𝒐𝒖𝒃𝒍𝒆 𝒕𝒉𝒆 𝒔𝒕𝒂𝒄𝒌 , 𝒆𝒍𝒔𝒆 𝒋𝒖𝒔𝒕 𝒊𝒏𝒄𝒓𝒆𝒎𝒆𝒏𝒕 𝒕𝒉𝒆 𝒕𝒐𝒑 𝒂𝒏𝒅 𝒑𝒖𝒔𝒉 𝒕𝒉𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕.

𝑨𝒕 𝒇𝒊𝒓𝒔𝒕 𝒘𝒆 𝒄𝒓𝒆𝒂𝒕𝒆 𝒐𝒃𝒋𝒆𝒄𝒕 𝒐𝒇 𝑺𝒕𝒂𝒄𝒌 𝒂𝒏𝒅 𝒅𝒆𝒄𝒍𝒂𝒓𝒆 𝒂 𝒗𝒂𝒓𝒊𝒂𝒃𝒍𝒆 𝒕𝒐 𝒅𝒆𝒄𝒊𝒅𝒆 𝒘𝒉𝒂𝒕 𝒔𝒉𝒐𝒖𝒍𝒅 𝒃𝒆 𝒄𝒂𝒑𝒂𝒄𝒊𝒕𝒚 𝒐𝒇 𝒕𝒉𝒆 𝒔𝒕𝒂𝒄𝒌 𝒊𝒏 𝒎𝒂𝒊𝒏 𝒇𝒖𝒏𝒄𝒕𝒊𝒐𝒏.