Although there are hundreds of cartesian/euclidean/square pathfinding visualizers, I have yet to come across one that is polar/non-euclidian/non-square, perhaps because it is less effective in depicting pathfinding—regardless, this project introduces pathfinding visualization to non-euclidian space and is a tool for visualizing pathfinding algorithms on a polar plane. To use it yourself,
The console is located at the top left of the application and contains 4 components: a label to display instructions and information about algorithms, a label to track the number of nodes checked, a label to display unweighted path length, and a label to display weighted path length.
The control panel is below the console and contains 6 components: a button to clear the map, a button to generate a map, a toolbox that contains tools to draw a map, a drop down menu to select an algorithm, a slider to set animation speed, and finally a button to initiate searching. Clicking the clear map button resets the color of each node back to white, and clicking the generate map button creates a maze with a random start, finish, and random walls. The toolbox contains radio buttons to select between drawing a start(green), a finish(red), walls(black), and using an eraser(sets nodes back to white). The drop down menu allows you to pick from dijkstra's algorithm, breadth-first search, and depth-first search, and updates the label that displays information about the algorithms in the console when selected. The slider controls the speed of the searching animation; the farther to the right the slider the quicker the animation. The search button initiates searching, but only works when there is a start and finish node marked on the grid and an algorithm selected. While searching, the control panel is disabled.
The following sections go over in detail each algorithm implementation. Nodes that are checked are blue and nodes that are part of the path are yellow.
Breadth-first Search explores equally in all directions. BFS is unweighted and guarantees the shortest unweighted path.
Depth-first Search traverses by exploring as far as possible down each path before backtracking. DFS is unweighted and does not guarantee the shortest unweighted or weighted path.
Dijkstra’s Algorithm prioritizes which paths to explore; instead of exploring all possible paths equally like breadth-first search, it favors lower cost paths. Dijkstra's is weighted and guarantees the shortest weighted path.
To better compare the three algorithms above, the gif below shows each algorithm pathfinding for the same map.
As seen in the visualizer, BFS finds the shortest unweighted path of 11. However, it does not take weights into account and does not find the shortest weighted path (finds a weighted path of 20.96), traveling left before going towards the origin. Dijkstra's, on the other hand, takes weights into account and finds the shortest weighted path of 11.53 by traveling towards the origin before traveling left. DFS is very ineffective as its property to go down a path as far as possible before backtracking makes it go in a very long spiral, finding an unweighted path length of 133 and a weighted path length of 367.32.
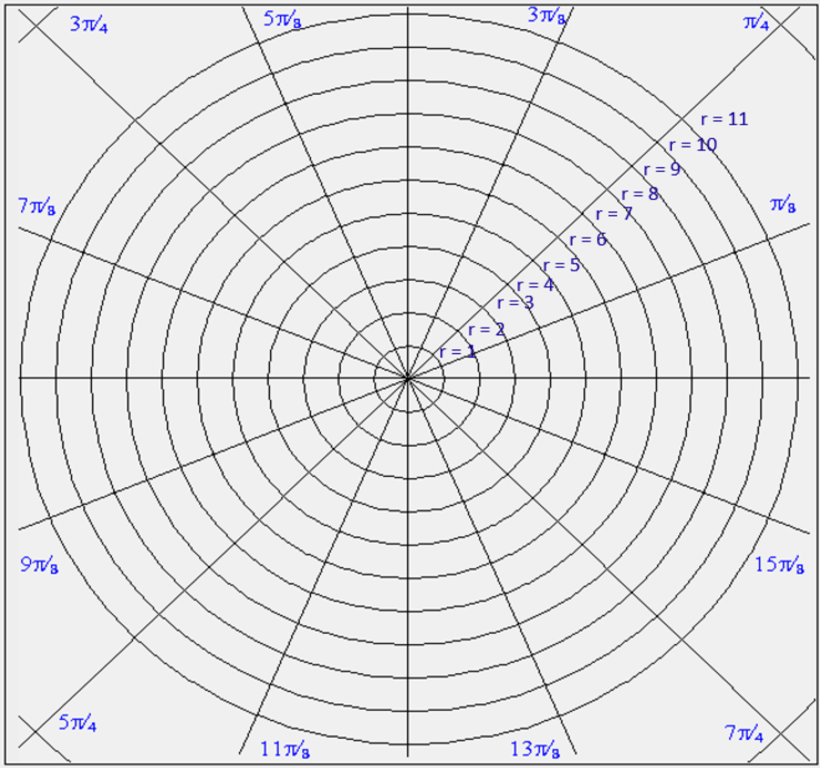
The weights of the edges of the graph are explained in detail below.
The graph/grid is undirected, but either weighted or unweighted depending on the algorithm selected. Dijkstra's algorithm uses weights while depth-first search and breadth-first search do not. To determine the numerical weights of the weighted graph/grid for dijkstra's algorithm, the measurements below were used.
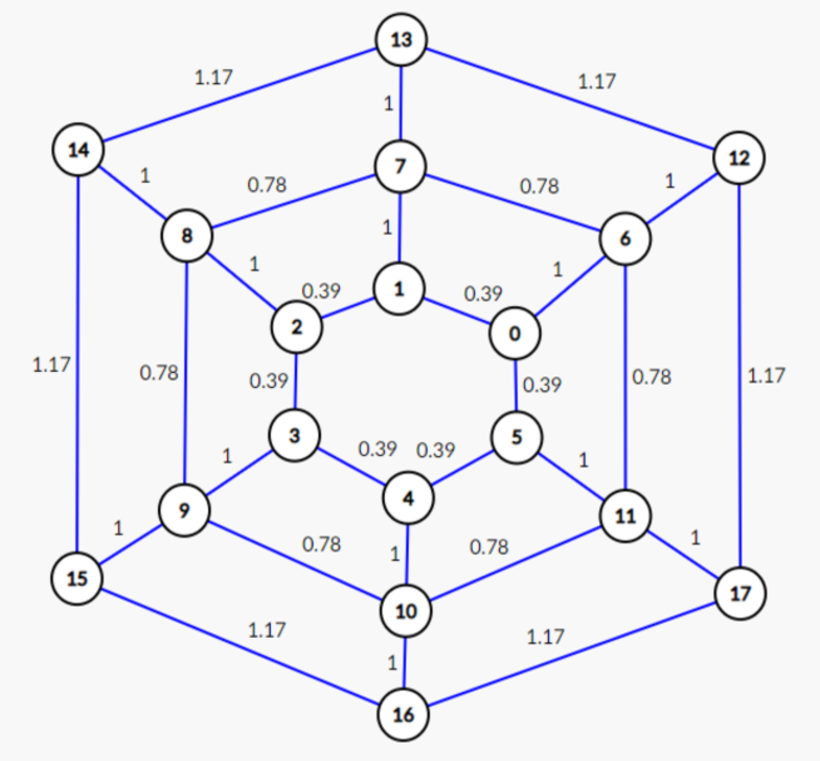
With these radii and angles, weights for edges that stem left and right from nodes were calculated with the arc length formula s = rθ, while weights for edges that stem forward and backward from nodes are 1 (because the distance from traveling forward and backward from nodes is constant). The following is a weighted graph that roughly represents the polar grid for dijkstra's.
Note that this graph is not the exact one used in the application, and that the actual graph has 16 nodes per circle(instead of 6), 11 circles(instead of 3), and possibly obstructions. However, the weights between edges in the image properly depict that traveling left and right between nodes farther away from the origin is more costly(because of a greater arc length), whereas traveling forward and backward between nodes is the same distance anywhere on the graph. Consequently, dijkstra's will choose the path that is closer to the center as going left and right is less costly when closer to the origin.
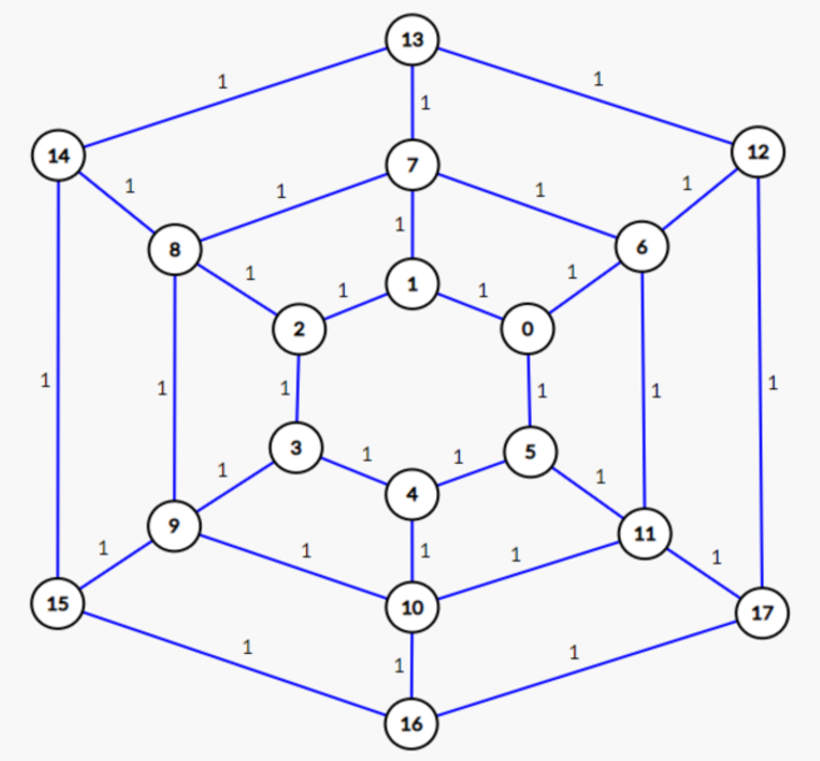
Since depth-first search and breadth-first search do not take weights into account, weights for all edges are 1. The following is an unweighted graph that roughly represents the polar grid for these algorithms.
Note again that this graph is not the exact one used in the application, and that the actual graph has 16 nodes per circle(instead of 6), 11 circles(instead of 3), and possibly obstructions.
A star implementation is in progress.